A felületi Au-dekorációs TEM technika 50 éves évfordulójára

Malicskó László (MTA-SZFKI)

A felületi Au-dekorációs módszer megjelenésének előzményei:

- 1920 és 1940 közt megjelent, Kossel-Stranski-, Volmer-Stranski-Kaisev-féle (2D magképződéses) kristálynövekedési elméletek

- A Taylor-Orowan-Polányi-féle kristályplaszticitás diszlokációs elmélete (1934),

- (BURGERS alapján, 1939) FRANK (1949) által felismert és BURTON, CABRERA FRANK által kidolgozott csavardiszlokációs, un. BCF növekedés elmélet (1951)

a kristályok határoló lapjain különféle, „elmélet-jellegzetes” monoatomos növekedési ill. deformációs felületi lépcső/réteg alakzatok jelenlétét "jósolták".

OM szintű próbálkozások az elméletek által jósoltakhoz hasonló felületi struktúrák láthatóvá tételére. Példák:

Maratás, mint dekoráció.

LiF két, maratott "tükör"-hasítási lapja (bal, jobb) – a jobboldali lap fotója a baléval azonos állásba átforgatva. A „tükör” maratási gödrök „fedésbe hozható” helyzete bizonyítja a gödrök (diszlokációk) nem-véletlen, előfordulását 1:1 megfeleltethetőségét, azaz diszlokáció vonal eredetűségét. Kb. 100x TOM-BFI (Gilman, Johnston,1957).

SiC (0001) növekedési lapja dekorálatlan „durva” lépcsős struktúrájának (a) és NH₄Cl-dekorált finom spirális növekedési lépcsős (b) normál OM 280x eredeti nagyítású képe. A "finom" dekoráció nm szintű "finom" lépcsőket tett láthatóvá (Lemmlejn, Gliki, 1954).

Közben. 1950-es években: HV-ban lecsapatott Au-magképződési vizsgálatok NaCl különfélekép előkezelt (100) hasítási lapjain (vékonyrétegek, szubsztrát).

Bassett (1958) megállapitása: NaCl (100) hasítási felületére nagyvákuumban néhány ML -nyi Au-t felpárologtatva néhány nm méretű Au-krisztallitok alakulnak ki, melyek C filmbe ágyazva TEM-ben látható, atomos, h = 0,3 nm magas felületi lépcsőket is dekorálni képesek. A dekorált lépcsők atomosságának igazolása (a röntgensugár és elektron hullám természete bizonyításához hasonlóan!):

A képen átlósan látszó, leszámlálhatóan n számú, Au-dekorált atomos lépcsőből álló hasítási lépcsőköteget keresztbe metsző, dekorált egyedi atomos csúszási lépcső nyoma a két térfélen egymáshoz képest az elméletileg jósolt n(a/2)-vel van eltolva, ahol a – a rácsállandó.

Bethge-iskola (1959-): kristályhibák vizsgálata (NaCl)

1. Kristályleépülés, növekedés nagyvákuumban (Keller).

Kiindulás: „Elemi” hasítási struktúra és leépülésének kezdeti stádiuma (300 C^o, 45 perc). --- Kossel-Stranski-folyamat.

A felület „kisimulása” után az elméleti modellek szerinti leépülés

kezdetei: 2D lyukmagok és koagulátumaik (Volmer-Stranski-Kaisev folyamat); csavardiszlokáción – kezdeti lépcsőgörbület és két csavarodás (Frank-folyamat). (Megjegyzés: szimultán!)

1.1.A 2D-magképződés és növekedési mechanizmus (2DN)

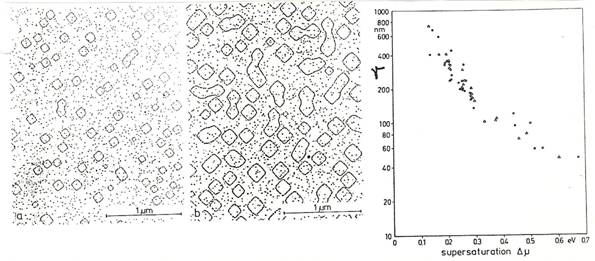
NaCl (100) lapjának gőzfázisú növekedés stádiumai 2DN mechanizmus szerint

a:  = 0,21 eV,       b:  = 0,21 eV         c: 2D magsugarak (r)

   0,5 ML növés után    0,8 ML növés után    r_k =/ hiperbolikus.

Éldiszlokáció mint permanens 2DN-hely.

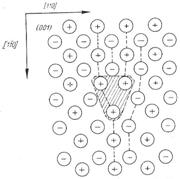NaCl (100) lapjára „kibukkanó” a/2(110) típusú éldiszlokáció körüli ionelrendeződés vázlata --- 2DN-re kedvező hely.

Éldiszlokációkon lokalizált, preferált 2D magképződéssel keletkező körlépcsős növekedési halmok kialakulási stádiumai NaCl (100) lapjain.

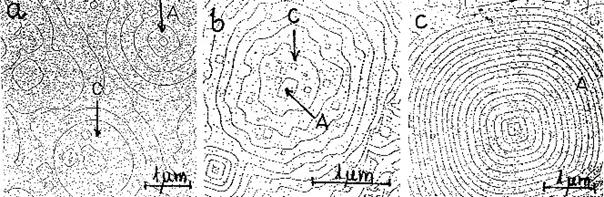
a) T = 347 C^o ,                b) T = 346 C^o ,                c) T = 313 C^o

= 0,14 eV                   = 0,30 eV                  = 0,20 eV

(Megjegyzés: 2DN-el szimultán „véletlen” 2DN a lépcsőteraszokon!)

1.2.Csavardiszlokációs CSD növekedési mechanizmus.

b=a(001) (a) ill. kettős b=a/2(001) (b) csavar- diszlokáció kibukkanási pontjából kiinduló „félvégtelen” két- ill. egyatomos felületi lépcsők vázlata.

Tipikus elemi növekedési/leépülési „spirál” lépcső formák Keller nyomán:

Egy fő és két „bezárt” b=a/2(001)  b=a(001) CSD

CSD körüli egyatomos lépcsősor.       körüli kétatomos lépcsősor.

  Két közeli azonos és  ellentétes fordulatú

b=a/2(001) CSD  lépcsősora.

Elméletileg a lépcsősorok lépcsőközi távolsága y₀ állandó, CSD-nél

y₀=4r_k ill. pontosabb számítások szerint  y₀=19.r_k . Reális növekedésnél/leépülésnél azonban a lépcsőtáv nem feltétlenül állandó lokális kémiai potenciál variációk miatt.

                Mesterséges hőmérséklet     Szennyező atomok okozta „V”

 Ingadozás okozta lépcső-     kontúrhibák éldiszlokáció körüli

köz távolsági fluktuációk       koncentrikus körlépcsőkön.

„Szabálytalan” négyzetes párolgási gödör egy – sokatomos lépcsőkkel, általában nagy kiterjedéssel (kb. mint a klasszikus maratási gödör).

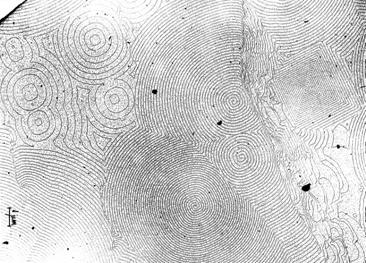
400 C^o-on 90

percig lepárolog-tatott NaCl felület lépcsős struktú-rájának áttekintő képe: „durva” hasítási lépcső elemiekre bomlása; kétatomos négyzetes, egy-atomos egyedi és kettős spirál; koncentrikus körlépcsők.

A lépcső-források „aktivitása” eltérő!

Elemi növekedési és párolgási lépcsők tangenciális mozgás sebessége lépcsőtáv függésének mérése „kettős-dekorációval” (Keller).

(350 C^o, 14 perc)

A BCF-elmélettel egyezésben!

Nem csak NaCl dekoráció!

Elektrolitikusan növesztett Ag egyristály (111) lapján Au-dekorált atomos spirállépcső (Klaua).

Megjegyzés: Au-n kívül más nemes fém és kristályos vegyület is lehet alkalmas dekoráló partner.

Nem csak lépcső-dekoráció! – felület-tartomány dekoráció.

Triglicinszulfát (TGS) ferroelektromos doménjeinek

46 C^o-on, 8 nm-es AgBr krisztallitekkel dekorált képe (Meyer).

2.Szemcsehatárok szerkezete (Scholz).

Geometriai elmélet:

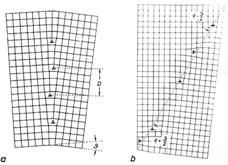Köbös primitív rácsnál un. „kis-szögű” szimmetrikus és nem szimmetrikus „tilt” típusú (éldiszlokációkból felépülő) szemcsehatárokon az éldiszlokációk elhelyezkedése. A diszlokációk un. vonalsűrűsége a dezorientáció szögektől függ.

Csavardiszlokációkból felépülő un. „twist” határok és a hasítási lapokon következményként várható atomos lépcső struktúra

sémája.

NaCl szemcsehatárainak hasítási és párolgási struktúrája.

NaCl (001) hasítási lapján egy vegyes kisszögű szemcsehatár jellegzetes nyomvonala. A függőleges ekvidisztáns Au-szemcsesor az éldiszlokációk kibukkanási helyeit (tilt komponens), az ekvidisztáns ferde lépcsők csavardiszlokációk hasítási nyomvonalai (twist komponens).

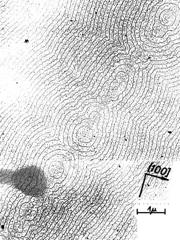
         Kisszögű csavardiszlokációs               és                                       éldiszlokációs

szemcsehatár jellegzetes leépülési lépcső-struktúrája.

A kis pettyezett körök nem jól látszó spirál-centrumokat jeleznek.

Mesterséges bikristály-határok diszlokáció struktúrája

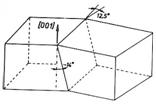
Egy 12,5^o-os bikristály vázlata és (001) hasítási lépcsőstruktúrája.

A két kristályrész g-g^, és g₁-g₁^, csúszási lépcsői direkt mutatják a két rész közti dezorientációt.

3.Oldatból növesztett mono és bikristályok növekedési mechanizmusának és benőtt hibáinak vizsgálata (Malicskó)

Pb:KCl monokristály és henger-bikristály makrofotója.

A monokristály lapon véletlenszerűen, a henger-bikristály lapján a „szemcsehatár” jellegzetes helyein sokatomos koncenrikus körlépcsős

domináns növekedési centrum(ok) alakulnak ki. Csernov elmélet: C_s(h)

Megállapítások: h(r) – monoton növekedő, Csernov-elméleti C_s(h)

szerint C_s(r) – monoton növekedő kell legyen, mely benőtt feszültség teret, diszlokációkat, repedést eredményez.

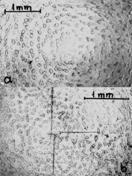
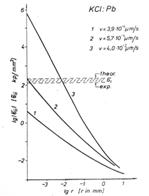
    1)

     2)

Domináns növekedési centrum(DNC)?

DNC közepének durva és finom lépcsős struktúrája.

Speciális diszlokáció- csoportok nagy kollektív forrás aktivitása.

Elemi növekedési lépcsők koagulációja?

Szabálytalan négyzetes lépcsők

magasságai, valószínűségi sűrűség függvényei

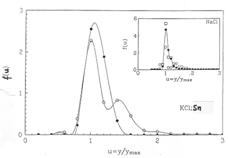
A CSD és 2DN növekedési mechanizmusok szimultán

működése (Bennema, Malicskó 1965-7)

Megjegyzés: inkoherens 2DN (Kleber) elvi lehetősége!

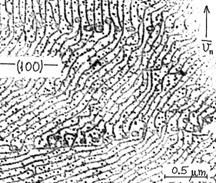
Inkoherensen illeszkedő növekedési rétegek okozta CSD –ós szemcsehatárok a kristály belsejében (un. „v-párhuzamos” metszet párolgási lépcső struktúrája).

Benőtt, szabálytalan határvonalú

inkoherens szemcse

körüli bonyolult párolgási lépcső struktúra (un. „v-merőleges” metszet).

Megjegyzés: csak a szemcsehatárok bizonyos szakaszai képeznek domináns növekedési/párolgási centrumokat!

Zárszó: A dekorációs szénreplika TEM módszer a pásztázó szondás mikroszkópia (SPM) megjelenéséig (1987) a felület nanométer szintű geometriai struktúrájának vizsgálatában kiemelkedő szerepet játszott.

Köszönetnyilvánítás

Dr.Gémesi József adjunktus úrnak – a kristályok világába bevezetésért,

Prof.Dr.Gyulai Zoltán akadémikusnak – az abban munkálkodás  lehetővétételéért,

Jeszenszky Béla tanár úrnak – a mikroszkópia megszerettetéséért,

Dr.Pócza Jenő és Dr.Morlin Zoltán tanár uraknak – Prof.Dr.Heinz Bethgével megismerkedésem lehetővé tételéért (1963, Warnemünde, Halle-IFE), hazai EM munkámban munkatársaik nyújtotta folyamatos segítőkészségéért.

Prof.Dr.Heinz Bethgenek és munkatársainak – az Au-dekorációs és egyéb EM technikák saját témáimra felhasználásában 30 éven át nyújtott segítségükért.