
Hell Miksa a tudománytörténetben mindmáig legismertebb nevű magyar csillagász. Munkásságát külföldön is elismeréssel emlegetik. Magyarul is sokat írtak róla; tőle azonban mindeddig szinte semmit sem olvashattunk (csupán néhány levele, valamint legnevezetesebb megfigyeléséről, a wardöi Vénusz-átvonulás észleléséről készült könyvének legizgalmasabb néhány lapja jelent meg magyarul).
Ez a kis gyűjtemény ízelítőt kíván nyújtani a kiváló jezsuita csillagász tudományos írásaiból és leveleiből. Terjedelmébe csak néhány, fontosabb vagy a szerzőre jellemzőbb részlet fér az életmű ránk maradt, hiányosan is tekintélyes részéből. Teljesebb képet Hellről csak egy sokkal bővebb válogatás nyújthatna.
Hell Miksa (Maximilian Hell) 1720 május 15-én született Selmecbányán. Eredeti családi neve Höll volt, később (1760-ban) változtatta Hellre.[1.] Apja kiváló bányamérnök volt, sok találmánnyal járult hozzá a selmeci bányászat fejlődéséhez. 23 gyermeke közül Miksa vitte a legtöbbre, de másik két fia, József és Ignác Kornél is kitűnő szakember volt a maga szakterületén, a bányászatban.
Hell Miksa középiskolai tanulmányait a selmeci gimnáziumban végezte. Ezután 1738-ban Besztercebányán belépett a jezsuita rendbe. Két noviciátusi évét Trencsénben töltötte, ahol kivált a rendi tanulmányok iránti érdeklődésével. 1741-től Bécsben tanult, először filozófiát, majd természettudományokat. Hamar megszerezte rendi elöljáróinak megbecsülését, s társainak felügyelője (manuductor) lett. 1743-tól matematikát tanult, s lefordította latinra J. CRIVELLI olasz nyelvű matematikai munkáját. Ezt kibővítette, javította, és 1745-ben kiadta. 1744-ben és 45-ben már saját csillagászati megfigyeléseket is közölt.
1745-ben a rend lőcsei gimnáziumába került tanárnak, majd 1748 és 1752 közt Bécsben hallgatott teológiát. Itt írt társai számára egy tudományos kisenciklopédia-félét (Adiumentum memoriae manuale chronologico-genealogico-historicum), melyet különböző országokban többször is kiadtak.
1751-ben szentelték pappá, és a harmadik próbaévre Besztercebányára helyezték. Innen irányította a nagyszombati csillagda építését, majd Kolozsvárra utazott tanárnak és az ottani csillagda építésének irányítására. Sokféle teendője mellett még katonai lelkész is volt.
A már tudományos nevet szerzett fiatal jezsuitát Mária Terézia 1755-ben kinevezte udvari csillagásznak (Astronomus Caesareo-Regius) a bécsi csillagdába. Itteni sokféle kötelezettségének is (tanítás, a felszerelés karbantartása és fejlesztése, csillagászati észlelések, csillagászati évkönyv kiadása, előadások tartása stb.) igen lelkiismeretesen tett eleget. Kapcsolatba került a kor legnagyobb csillagászaival, akik megfigyelései gondossága miatt nagyra becsülték. Közben további magyarországi csillagvizsgálók alapítását is segítette, így az egri és a budai obszervatórium tervezésében és felszerelésük beszerzésében is részt vett.
VII. Keresztély dán király a Vénusznak a Nap előtti 1769. jún. 3-i átvonulása megfigyelésére Vardöbe hívta meg Hellt. Hell és segítője, SAJNOVICS JÁNOS 1768 ápr. 28-án indultak útnak; sokrétű természettudományos megfigyelést végeztek mind útjuk során, mind pedig Vardöben. Eközben Hell kipróbálta a földrajzi szélesség (tkp. a sarkmagasság) mérésére feltalált igen fontos (és igen pontos) módszerét, amely ma Horrebow-Talcott-eljárás néven ismeretes és használatos. Az útjuk céljául szolgáló mérést nagy szerencsével sikeresen elvégezték. (Közben Sajnovics fölfedezte a magyar-lapp nyelvrokonságot.) Ez az expedíció tette Hell nevét világhírűvé.
A jezsuita rend 1773-as eltörlése miatt megszűnt a rend részéről Hellnek nyújtott anyagi és szellemi támogatás. Hell a világi papság kötelékébe lépett, de mindvégig reménykedett rendje újjáéledésében (amit azonban már nem érhetett meg). Ha nem is zavartalanul, de folytatta sokoldalú tudományos kutatásait többek között a néprajz, földrajz, történelem, teológia, fizika tárgyköreiben - természetesen a csillagászat mellett. 1774-ben a naptár ügyében nyújtott be egy tervezetet a bécsi udvarhoz. Ennek eredményeképpen egy 1776-os császári rendelet alapján Hell gondoskodhatott egy csillagászati naptár kiadásáról.
Az egyre szaporodó, egyedül végzett munka aláásta egyébként sem szilárd egészségét. 1792 tavaszán meghűlt, s lázas, hurutos megbetegedéséből már nem gyógyult fel. 1792. április 18-án, 72 éves korában hunyt el.


Ez utóbbi arab számjegyekkel felírt évszámokat
olvashatunk még ma is a legtöbb templomon és
régebbi épületeken Ausztria és Magyarország-szerte,
legfőképpen pedig Erdélyben azokon a helyeken,
amelyeket Saxoniainak neveznek. Pl. az épületek építésének
évét így olvassuk:  ,
vagy
,
vagy  ,
vagy
,
vagy  , amit senki más nem képes megérteni, mint csak az igen
művelt olvasó.
, amit senki más nem képes megérteni, mint csak az igen
művelt olvasó.
A mai római számjegyek, amelyeket közönségesen latin betűkkel írunk

Ahogyan ma a műveletlen nép, úgy a római nép elöljárói, akik az arithmeticát még nem ismerték, számokkal kifejezhető dolgaikat vonalkákkal, azaz vesszőcskékkel jelölték, illetve fejezték ki. Pl. ha azt kívánták kifejezni, hogy 20 mérő búzát akarnak eladni, ezt így írták: | | | | | | | | | | | | | | | | | | | |, és az ilyen vonalkák segítségével fejezték ki, bármekkora nagy számot akartak is leírni. De az ilyen, tudniillik nagyon hosszú és ügyetlen számjelölési mód, ellenszenvessé tette a nem egyszerű jelölést és számolást. Így hát valamely élesebb eszűek kigondoltak valamit ugyanezen, a gyakorlatban már bevett vonalkák rövidebb leírásának módjáról, hogy ugyanis két vagy három vonalkával, egymáshoz képest különféleképpen hajlóval, a hosszabb számot rövidebben is visszaadhatják, és bevezették ezeket az emberek közös megállapodása alapján a polgári használatba. Úgy látszik tehát, hogy a rövidebb úton, a négyes számtól kezdve, így indultak el.
1. Az | | | | | öt vesszővel jelölt ötös számot
két, egymás felé hajló vonalkával
jelölték, így:  , amit hogy gyorsabban leírhassák,
összekapcsolták így: v; és innen ered
az öt mai jele (V) vagy betűje (v).
, amit hogy gyorsabban leírhassák,
összekapcsolták így: v; és innen ered
az öt mai jele (V) vagy betűje (v).
2. Az ötös számnak ez a  formája
jobbról hozzákapcsolt függőleges vonalkákkal
fejezte ki a többi számot a tízesig, vagyis
a tízes számig; s minthogy kétszer öt
az tíz, az ötösnek két
jelével, amelyeket csúcsukkal egymás felé
állítottak, tehát így:
formája
jobbról hozzákapcsolt függőleges vonalkákkal
fejezte ki a többi számot a tízesig, vagyis
a tízes számig; s minthogy kétszer öt
az tíz, az ötösnek két
jelével, amelyeket csúcsukkal egymás felé
állítottak, tehát így:  , amit a gyorsabb
leírás kedvéért így alakítottak:
X. Innen eredhet a ma használatos jel (X) vagy betű
(x).
, amit a gyorsabb
leírás kedvéért így alakítottak:
X. Innen eredhet a ma használatos jel (X) vagy betű
(x).
E négy vonalkával | | | |, az ötös
 és
a tízes
és
a tízes  jelével a rómaiak megtalálták
a kisebb számok rövid jelölésére
az utat, de a nagyobb számokéhoz még nem,
ezért további számjegy-formákat találtak
föl.
jelével a rómaiak megtalálták
a kisebb számok rövid jelölésére
az utat, de a nagyobb számokéhoz még nem,
ezért további számjegy-formákat találtak
föl.
3. Így az ötös szaporítása
által, amikor




 , azaz ötször tíz, ötven
lett, két egyenes vonalat ilyen helyzetbe rakva:
, azaz ötször tíz, ötven
lett, két egyenes vonalat ilyen helyzetbe rakva:  [új]
alakot hozva létre, az ötvenet jelölték,
amit hogy gyorsabban kialakíthassanak, így
írták:
[új]
alakot hozva létre, az ötvenet jelölték,
amit hogy gyorsabban kialakíthassanak, így
írták: 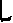 ,
amiből a mai L jel származik.
,
amiből a mai L jel származik.
4. Továbbá, mivel a száz kétszer
ötven, két ötvenes számjelet 
 ebben
a helyzetben:
ebben
a helyzetben:  , mintegy megfordítva az egyiket:
, mintegy megfordítva az egyiket:  , a másikat
pedig egyenesen:
, a másikat
pedig egyenesen: 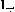 összekapcsolva fejezték ki, amit
hogy gyorsabban írhassanak le, így alakították:
összekapcsolva fejezték ki, amit
hogy gyorsabban írhassanak le, így alakították:  , majd
, majd 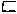 , és még gyorsabban írhatóan
ebbe:
, és még gyorsabban írhatóan
ebbe: 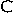 ment át, igen hasonlóan a mai C betűhöz,
ami a százat jelöli.
ment át, igen hasonlóan a mai C betűhöz,
ami a százat jelöli.
5. Mivel ötször száz ötszáz,
az ötször ismételt százas alak helyett
két, szembe fordított százas jellel
helyettesítették:  ,
ami gyorsabban leírva ilyen:
,
ami gyorsabban leírva ilyen:  ,
aztán meg ilyen:
,
aztán meg ilyen:  vagy hasonlóan
vagy hasonlóan 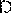 ,
végül ilyen formába:
,
végül ilyen formába:
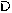 , a D betűhöz hasonló és ma is használt
formába ment át.
, a D betűhöz hasonló és ma is használt
formába ment át.
6. Ugyanígy, mivel kétszer ötszáz ezret
ad, két ötszázas jelet szembefordítva
helyeztek el:  , alakították ki az ezrest,
és gyorsabban írva így:
, alakították ki az ezrest,
és gyorsabban írva így:  vagy
vagy  ,
gyorsabban
,
gyorsabban  , vagy
, vagy
 , vagy
, vagy  , amely utolsó alak, amely nagyon hasonlít
a kis m betűhöz, alkalmat adott az írnokoknak,
hogy ezt szebben formálják egy nagy M betűvel,
amit ma is használunk. Ezeket a különféle
formákat áttekintésre alább adom.
, amely utolsó alak, amely nagyon hasonlít
a kis m betűhöz, alkalmat adott az írnokoknak,
hogy ezt szebben formálják egy nagy M betűvel,
amit ma is használunk. Ezeket a különféle
formákat áttekintésre alább adom.
| Az egyszerűbb formák: Gyorsabban írva: Sokkal gyorsabban: Leggyorsabban: amiből eredő maiak: |  |
Ezzel a hét formával (jellel) jelölt a maga addigi egyszerűségében boldog római nép minden számot, amelyekhez a találékony utókor bizonyos másokat is hozzávett, amelyek közül egyeseket Cl. Poëtius Arithmeticájából kiválasztva adunk.
Az  vagy
vagy  vagy
vagy 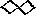 jelet használták az 1000 helyett.
jelet használták az 1000 helyett.
Az 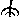 vagy
vagy  vagy
vagy 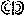 jelezte a 10 000 számot.
jelezte a 10 000 számot.
Két  vagy
vagy  jelölte a kétszer 10 000, azaz 20
000 számot.
jelölte a kétszer 10 000, azaz 20
000 számot.
Ha az ezres jelét (  ) eléjük tették,
pl.
) eléjük tették,
pl.  , akkor úgy értették, hogy ki kell vonni,
tehát 19 000-et jelent.
, akkor úgy értették, hogy ki kell vonni,
tehát 19 000-et jelent.
Az  vagy
vagy  jel 20-at jelöl, és az
jel 20-at jelöl, és az  harmincat, aminek
későbbi használatából eredtek
az aranykori szerzők által is használt következő
jelek.
harmincat, aminek
későbbi használatából eredtek
az aranykori szerzők által is használt következő
jelek.

A matematika módszeréről
I. A matézis (görög szóval 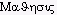 , tudomány,
vagy antonomasiát alkalmazva disciplina) a mennyiség
tudománya. Két fajtája a Tiszta és
a Kevert matematika [mathesis pura et mixta]. A tiszta matematika
a minden anyagitól mentes mennyiség tudománya,
amelynek tárgya minden, ami megszámolható
vagy mérhető; ide tartozik az algebra a numerikus
aritmetikával együtt, valamint a tiszta geometria.
Kevert matematikának mondják a matematikának
azt a részét, amely fizikai anyaggal kapcsolatos;
ilyenek a kevert geometria, a statika, mechanika, hidraulika
stb. A tiszta matematika a legbiztosabb tudomány, a
kevert viszont csak a matematikai forma szerint biztos, de nem
az anyag szerint.
, tudomány,
vagy antonomasiát alkalmazva disciplina) a mennyiség
tudománya. Két fajtája a Tiszta és
a Kevert matematika [mathesis pura et mixta]. A tiszta matematika
a minden anyagitól mentes mennyiség tudománya,
amelynek tárgya minden, ami megszámolható
vagy mérhető; ide tartozik az algebra a numerikus
aritmetikával együtt, valamint a tiszta geometria.
Kevert matematikának mondják a matematikának
azt a részét, amely fizikai anyaggal kapcsolatos;
ilyenek a kevert geometria, a statika, mechanika, hidraulika
stb. A tiszta matematika a legbiztosabb tudomány, a
kevert viszont csak a matematikai forma szerint biztos, de nem
az anyag szerint.
II. A matematikai módszer az a mód vagy valamely különleges eljárás, amelyet a matematika az igazságainak fölfedezésére, bizonyítására, átadására használ. Két részre osztható, éspedig az analitikus és a szintetikus módszerre. Az analitikus vagy szétbontó módszer az igazságok megtalálására, fölfedésére szolgál; a szintetikus vagy egyesítő pedig mindazt, amit az analízis segítségével találtunk, rendszerbe szedi, és egyik igazságot a másikhoz kapcsolja úgy, hogy egymástól mintegy összeláncolva függjenek; ez szolgál a matematika tételeinek átadására. Így a szintetikus módszer a következőket alkalmazza: I. Definíciók. II. Posztulátumok. III. Axiómák. IV. Tapasztalatok. V. Hipotézisek. VI. Föltevések. VII. Bizonyítások. VIII. Tételek. IX. Problémák. X. Porismák vagy Lemmák [segédtételek]. XI. Korolláriumok [következmények]. XII. Scholia [megjegyzések].
III. Definíció a megkülönböztető ismertetése vagy kifejtése a dolognak vagy névnek, amiről szó van. Pl. Szám az egységek rendezett sokasága.
IV. Posztulátumnak nevezzük azt, amiről megköveteljük, hogy valami másból könnyen levezethető legyen számunkra, hogy lehetséges. Pl. egy pontból a másikhoz egyenest húzni.
V. Axióma ( , hitelt érdemlő)
az olyan igazság, amely kellően megértve
a kifejezéseket, magától vagy a szavakból
nyilvánvaló, vagy a természet fényében
ismert. Pl. Az egész nagyobb, mint a rész.
, hitelt érdemlő)
az olyan igazság, amely kellően megértve
a kifejezéseket, magától vagy a szavakból
nyilvánvaló, vagy a természet fényében
ismert. Pl. Az egész nagyobb, mint a rész.
VI. Hipotézisek ( , helyettesítés)
dolgok, vagy dolgoknak emberi megállapodással
elfogadott tetszőleges jelei, pl. ha az egyenlő
szó helyett a = jelet használjuk, vagy az 5 szám
helyett a vagy b betűt; és hasonlóak
a csillagászatban a Nap helyett
, helyettesítés)
dolgok, vagy dolgoknak emberi megállapodással
elfogadott tetszőleges jelei, pl. ha az egyenlő
szó helyett a = jelet használjuk, vagy az 5 szám
helyett a vagy b betűt; és hasonlóak
a csillagászatban a Nap helyett  , a Hold
helyett
, a Hold
helyett  stb.
stb.
VII. Tapasztalat (experientia) valamely külső észlelet vagy belső megismerés hasonló eredménye, illetve az ebből fakadó ismeret, pl. midőn a csillagok, melyek nap közben nem látszanak, a nap lenyugvása után, derült éjjel, megláthatók. A tapasztalatok tehát csak az egyszerű dolgok ismert észleletei.
VIII. Föltevés valamely föltett igazság vagy gyakorlat világos és határozott kijelentése; így kétféle lehet: spekulatív vagy teoretikus, illetve gyakorlati. A spekulatív föltevés valamely igazság világos és határozott kijelentése, vagyis hogy bizonyos feltételek mellett vagy önmagában mely dolog teljesülhet, s mely nem. Pl. ha két számot összeszorzunk, ugyanazt a szorzatot kapjuk, ha az elsőt a másodikkal, vagy ha a másodikat az elsővel szorozzuk. Gyakorlati föltevésről beszélünk, ha valamit meg szándékozunk tenni vagy végre akarunk hajtani. Pl. Numerikus összeadást elvégezni, azaz számokat összeadni. Továbbá mindkétfajta föltevés lehet föltételes, azaz hipotetikus, avagy abszolút. Föltételes, amely kijelent egy igazságot vagy valaminek az elvégzését kívánja meg bizonyos feltételek mellett; pl. Ha négy mennyiség arányos, akkor a két külsőnek szorzata egyenlő a belsők szorzatával. Itt tehát az arányosság feltétele mellett jelenti ki a kültagok szorzatának a beltagok szorzatával való egyenlőségét. Abszolút, ha semmiféle föltételt ki nem kötve jelenti ki, pl. amit a szorzás létrehoz, azt az osztás megszünteti.
IX. Bizonyítás már ismert elvekből levezetett rövid érvelés, amely az értelmet meggyőzi, hogy állítsa vagy tagadja azt, amit a föltevésben vagy a kérdésben állítunk vagy tagadunk.
X. Tétel ( , speculatio) egy általános
spekulatív föltevésből és egy
bizonyításból álló egység
(complexum), vagy egy hasonlóan állított
és bizonyított igazság. Pl. ha föltesszük
azt az igazságot, hogy amit a szorzás létrehoz,
azt az osztás megszünteti, és ugyanakkor
ezt a hozzácsatolt bizonyítással igazoljuk,
akkor ez az egész együtt egy tétel. A tétel,
pontosabban a bizonyítás ezzel a jellel végződik:
Q. E. D., ami azt jelenti: quod erat demonstrandum, vagyis
hogy amit igazolni kellett.
, speculatio) egy általános
spekulatív föltevésből és egy
bizonyításból álló egység
(complexum), vagy egy hasonlóan állított
és bizonyított igazság. Pl. ha föltesszük
azt az igazságot, hogy amit a szorzás létrehoz,
azt az osztás megszünteti, és ugyanakkor
ezt a hozzácsatolt bizonyítással igazoljuk,
akkor ez az egész együtt egy tétel. A tétel,
pontosabban a bizonyítás ezzel a jellel végződik:
Q. E. D., ami azt jelenti: quod erat demonstrandum, vagyis
hogy amit igazolni kellett.
XI. Probléma (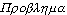 , föltevés, avagy
elvégzendő dolog) egy olyan komplexum, amely
áll egy gyakorlati föltevésből,
vagyis valamiből, amit el kell végezni, egy megoldásból,
amely a dolog elvégzésének módját
mutatja meg, és egy bizonyításból,
amely megmutatja, hogy az adott megoldás valóban
azt adja, amit akartunk. A megoldás ezzel a jellel
szokott végződni: Q. E. F., ami azt jelenti: quod
erat faciendum, vagyis hogy amit csinálni kellett.
, föltevés, avagy
elvégzendő dolog) egy olyan komplexum, amely
áll egy gyakorlati föltevésből,
vagyis valamiből, amit el kell végezni, egy megoldásból,
amely a dolog elvégzésének módját
mutatja meg, és egy bizonyításból,
amely megmutatja, hogy az adott megoldás valóban
azt adja, amit akartunk. A megoldás ezzel a jellel
szokott végződni: Q. E. F., ami azt jelenti: quod
erat faciendum, vagyis hogy amit csinálni kellett.
XII. Porisma (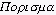 ,
,  , „átjáró")
megelőző tétel vagy premissza valamely következő
tételhez, vagy valamely lényegesen könnyebb
vagy rövidebben igazolható probléma, lemmának
is nevezzük. (
, „átjáró")
megelőző tétel vagy premissza valamely következő
tételhez, vagy valamely lényegesen könnyebb
vagy rövidebben igazolható probléma, lemmának
is nevezzük. ( , átvétel vagy előre
adott).
, átvétel vagy előre
adott).
XIII. Korolláriumok olyan igazságok vagy gyakorlatok, amelyek a definíciókból, axiómákból, tételekből vagy problémákból maguktól folynak, bármilyen egyszerű újabb bizonyítás nélkül.
XIV. Scholia  olyan megjegyzések a definíciók,
föltevések, korolláriumok stb. után,
amelyek a homályosabb részeket megvilágítják,
a kételyeket feloldják, bevezetnek a tan használatába,
valamely ismeretet adnak elő, vagy valamely mást
hoznak fel, amit hasznos tudni, vagy ilyenre alkalmasan emlékeztetnek.
olyan megjegyzések a definíciók,
föltevések, korolláriumok stb. után,
amelyek a homályosabb részeket megvilágítják,
a kételyeket feloldják, bevezetnek a tan használatába,
valamely ismeretet adnak elő, vagy valamely mást
hoznak fel, amit hasznos tudni, vagy ilyenre alkalmasan emlékeztetnek.
XV. E módszerben használatosak még paragrafus-számok is, hogy ezek segítségével, más helyeken használt neveket vagy igazságokat emlékezetünkbe idézni könnyebb legyen, ha kiestek volna, és hasonlóan, hogy elzárjuk ugyanazon dolgok vagy definíciók hosszas ismétlésének útját.
XVI. Ez a matematikai módszer megköveteli, hogy mindenekelőtt a szavakat és minden dolgot világosan és határozottan definiáljunk, előrebocsássuk az axiómákat, hipotéziseket és posztulátumokat, ha azokra szükség lesz, azután a kérdéses dolog mibenlétét is hasonlóan határozottan, világosan és a lehető legrövidebben tűzzük ki, azaz legyen a föltevés világos és határozott; a föltevést kitűzve azt, amit kitűztünk, és ugyanazon feltételek mellett, nem egyebet, röviden és világosan mutassunk meg. A bizonyításokban semmit ne használjunk, amit már előbb nem mutattunk meg, definiáltunk vagy kimondtunk; arra igen ügyelnünk kell, nehogy valami fölöslegeset is bevezessünk, de azért bevezethetünk egy és más észrevételt vagy szillogizmusból eredő következtetést, amely egyenértékű valamivel, amit előre elmondtunk. Ezekből hasznos korolláriumokat vezethetünk le, és scholionokat fűzhetünk hozzájuk, ha kell.
XVII. A propositiok vagy tételek rendjét körültekintően meg kell vizsgálnunk, hogy a lehető legegyszerűbbek és legkönnyebbek álljanak elöl, amelyekből a magasabbakhoz mint valami lépcsőn lehessen haladni, és ebben a haladásban a propositiok és az igazságok egymást olyan összefüggően kövessék, hogy a következő szükségképpen következzék az előbbiből, és úgy függjenek egymástól, hogy az utóbbiak az előbbiek nélkül ne következhessenek. Erről az igaz matematikai módszerről, amit itt érintőlegesen mutattunk meg, bővebbet láthatunk R. P. Philippus Steinmeyer S. J. Regulae prae cipuae methodi Mathematicae, seu scientificae [A matematikai vagy tudományos módszer legjobb szabályai] cím alatt Augsburgban 1750-ben megjelent elegáns művecskéjében; ugyanilyen a kitűnő Wolf Christian De Methodo Mathematica brevis commentatio [A matematikai módszer rövid tanulmányozása], az ő „Matematika alapjai"-jának elején.
I. fejezet
Az Analysis egész művészetének axiómái,
föltevései, általános gyakorlatai
212. Egyenlőségnek mondjuk az olyan algebrai kifejezést, amely az = jel közbeiktatásával kifejezi, hogy bizonyos, valahogyan adott mennyiségek egymás közt egyenlők, vagy egyenlők nullával: pl. ax + c = ab - d, vagy 3 + 5 - 2 = 6, vagy ax - ab = 0.
213. Az egyenlőség kifejezése tehát kifejezi, hogy az összes együtt fölvett és az = jel elé helyezett mennyiség egyenlő az ugyanígy együtt vett és a = jel mögé helyezett mennyiség értékével, vagy ami ugyanaz, hogy a = jel bal oldalán álló mennyiségek egyenlők a = jel jobb oldalára tett mennyiségekkel, amint ez nyilvánvaló az előbb mondottakból.
214. Az egyetlen közvetítő eszköz, amelyet az Algebra a mégoly elvont kérdések megoldására is használ, az egyenlet, avagy az egyenlőség kifejezése, az egész Analízis mestersége az egyenlőségek megtalálásában áll, és az adott egyenletnek egy ismeretlen mennyiségre (a mennyiségek egyenlőségének axiómái alapján történő) redukálásának mesterségében, úgy, hogy az egyenlet egyik oldalán csak egyetlen ismeretlen mennyiség szerepeljen, minden más, ismert vagy ismeretlen mennyiség nélkül, az egyenlet másik oldalán pedig tiszta ismert mennyiségek legyenek; amit hogy mi módon lehet helyesen elérni, a kérdések megoldásának általános mesterségét öt műveletre osztom, amelyekben ha a kezdő Analista jól begyakorolja magát, akkor neki semmi olyan nehéz probléma nem lehet, aminek megoldását, e műveletek segítségével, ne tudná megadni. Az Analista első művelete legyen: I. Az adott kérdés minden körülményének alapos vizsgálata, illetve az adott kérdés mibenlétének teljes, alapos megértése. II. A mennyiségeknek, mind az ismerteknek, mind az ismeretleneknek az ábécé betűivel való alkalmas jelölése. III. Az egyenlet megtalálása és felírása. IV. Az egyenlet redukálása, és V. A redukált egyenlet numerikus megoldása, vagy különösen alkalmas alakra hozása.
215. A megoldandó kérdés minden feltételének és körülményének alapos vizsgálata.
I. Az Analista, mielőtt egy kérdést megold, pontosan állapítsa meg a kérdés lényegét, azaz hogy mit kell keresni; amit megállapítván
II. Gondosan fejtse ki a megoldandó kérdésben foglalt feltételeket és körülményeket.
III. Keresse meg az ismert és ismeretlen mennyiségeket, hogy mi van adva, és mi rejtőzik ismeretlenül.
IV. Igyekezzék megérteni, melyik az az ismeretlen mennyiség, amelytől a probléma megoldása függ, és hogyan függenek össze ezzel a többi mennyiségek.
V. Mely mennyiségek (legyenek bár ismertek vagy ismeretlenek) egyenlők vagy legalább arányosak egymással a problémában adott feltételek szerint. Mindezt helyesen megértve térjen át az Analista a II. műveletre.
216. Mind az ismert, mind az ismeretlen mennyiségeknek az ábécé betűivel való alkalmas jelölése.
I. Az ismert mennyiségeket az ábécé első, az ismeretleneket az utolsó betűivel jelölje, mint már említettük.
II. Ha több olyan mennyiség (akár ismert, akár
ismeretlen) fordul elő, amelyek a diszkusszió szerint
bizonyos ismert arányban vannak egymással, ezeket
kevesebb betűvel fejezhetjük ki, s ezt tegyük
meg legelőször a redukció műveletének
megkönnyítésére; hogy ha pl. adott két
ismeretlen mennyiség, x és y, de tudjuk,
hogy y az x kétszerese, akkor y helyett
2x-et írok, ugyanígy ha y az x
fele, akkor jobb, ha  -vel jelöli az Analista, mint ha y-nal,
és így tovább.
-vel jelöli az Analista, mint ha y-nal,
és így tovább.
III. Az elvégzett jelölést a lap valamelyik szélére külön és távolabb (felírva a kérdésben használt szavakkal is, közbeiktatva az = jelet) jegyezze föl magának az Analista, részint nehogy elfelejtse, hogy melyik betűvel melyik mennyiséget jelölte, részint hogy a redukált egyenlet megoldása rendben menjen.
217. Az ismert és ismeretlen mennyiségek egyenlet formájába helyezése, vagyis a megtalált egyenlet felírása.
I. Megfelelően megvizsgálva az adott kérdés feltételeit, elvégezve a mennyiségek jelölését, ki fog tűnni, mely mennyiségek (akár ismertek, akár ismeretlenek) egyenlők vagy legalább arányosak; tekintet nélkül arra, hogy ismertek vagy ismeretlenek, az ismeretleneket és az ismerteket is a kérdések feltételei alapján vegyesen rendezze az egyenletbe; vagy ami ugyanaz, a kérdést latin vagy bármely más nyelvről a jelek és hipotézisek [jelölések] segítségével algebrai nyelvre fordítsa és így fejezze ki az Analista; ez a kifejezés lesz a kívánt első egyenlet, amit a redukció műveletében fel fog használni.
II. Alakítson annyi egyenletet a kérdés feltételeiből, ahány különböző ismeretlen mennyiséget talált, kivéve a határozatlan egyenletek esetét, melyekről később.
218. Amint az első egyenlet megtalálása és felírása éles és finom elmét kíván az Analistától, és ez (bárha igen nagy munkával) a próbakő, melyen az Analista őszintén próbára teheti ítélőképességét, úgy a megtalált első egyenlettel (amit mindazonáltal az Analista élesen látó elméje az adott kérdés feltételeiből könnyen kialakít) mi sem könnyebb, mint (a redukció műveletével) megtalálni a kérdés megoldását, és megtalálván felírni azt.
219. Az első egyenletek egyetlen egyedülálló ismeretlenre redukálása.
Ügyeljenek a kezdő Analisták, hogy e művelet végső célja az egyenlet mindkét oldalán egyenlő mennyiségeket használva az egyenletet úgy átalakítani ellenkező műveletekkel, hogy az egyik oldalon ismeretlen mennyiség jelenjék meg minden más, ismert vagy ismeretlen mennyiség nélkül, a másik oldalon pedig csupa ismert mennyiség, bármely ismeretlennek odakeveredése nélkül; amit hogy helyesen végezzenek az Analisták az axiómák és a kicsit később közlendő szabályok szerint, szeretném, hogy a következő általános szabályt vegyék észre és véssék agyukba, tudniillik.
Az egyenlet egyik oldalával végzett bármely műveletet az egyenlet másik oldalával is végezzük el, kivéve a metathesist [helyettesítést], mint alább kimutatjuk. Így a következő axiómákat, amelyekben a redukció szabályai vannak rögzítve, az Analista különösen vésse emlékezetébe.
A (MIND EGYENLŐ, MIND NEM EGYENLŐ) MENNYISÉGEK AXIÓMÁI
220. I. Bármi önmagával hasonló és egyenlő, mint a = a, vagy 3 + 2 = 5.
221. II. Ha két mennyiség egyenlő egy harmadikkal, akkor egymással is egyenlők, mint ha a = x és b = x, akkor a = b is igaz, vagy ha 3 + 2 = 5 és 7 - 2 = 5, akkor 3 + 2 = 7 - 2 is igaz.
222. III. Egyenlőt egyenlővel, vagy egyenlőket egyenlőkkel helyettesíteni szabad, mint pl. ha x = y és y = a, akkor x = a is igaz.
223. IV. Ha egyenlőkhöz egyenlőt vagy egyenlőket adunk, egyenlők maradnak, mint ha a = x, és mindkét oldalhoz hozzáadunk b-t, akkor a + b = x + b is igaz, ugyanígy ha a = x és c = d, akkor a + c = x + d is igaz.
224. V. Ha egyenlőkből egyenlőket vagy egyenlőt kivonunk, egyenlők maradnak, mint ha a = x, és mindkét oldalból kivonunk c-t, akkor a - c = x - c, ugyanígy ha a = x és c = d, akkor a - c = x - d is igaz.
225. VI. Ha egyenlőket egyenlővel szorzunk, a szorzatok egyenlők maradnak, mint ha a = x és mindkét oldalt b-vel szorozzuk, ab = xb is igaz.
226. VII. Ha egyenlőket egyenlőkkel osztunk, a hányadosok
is egyenlők maradnak, mint ha a = x és
mindkét oldalt c-vel osztjuk,
 is igaz.
is igaz.
227. VIII. Ha egyenlőket egyenlőkkel szorzunk, a
szorzatok egyenlők maradnak, mint ha a = x
és c = d, akkor ac = xd is
igaz; hiszen ac = cx és cx = xd
a 225. § szerint, tehát ac = xd a 222.
§ szerint. Ugyanígy [bizonyítható, hogy]
ha egyenlőket egyenlőkkel osztunk, a hányadosok
egyenlők maradnak, mint ha a = x és
c = d, akkor
 is igaz.
is igaz.
228. IX. Egyenlő mennyiségeket egyenlő hatványra emelve egyenlők maradnak, mint ha a = x, akkor a2 = x2 vagy a3 = x3 is igaz.
229. X. Egyenlő hatványra emelt egyenlő mennyiségekből
ugyanolyan kitevőjű gyököt vonva egyenlők
maradnak, mint ha aa = xx, akkor
 , vagyis
a = x.
, vagyis
a = x.
230. XI. Ha nem egyenlőkhöz egyenlőket adunk, vagy nem egyenlőkből egyenlőket kivonunk, ugyanígy ha nem egyenlőket egyenlőkkel szorzunk vagy osztunk, az összegek, különbségek, szorzatok és hányadosok nem egyenlők maradnak.
De satellite Veneris a Maximiliano Hell - S. J. Astronomo Caesareo-Regio Universitatis Vindobonensis. Viennae, typis et sumptibus Joannis Thomae de Trattnern, Caes. Reg. Maj. Aulae Typographi et Bibliopolae. MDCCLXV.
Non semper ea sunt, quae videntur; decipit
Frons prima multos; rara mens intelligit,
Quod interiore condidit cura angulo.
Phaedrus in Prologo ad Lib. IV.[6.]
Mivel ez az általam kilenc évig csendben visszatartott anyag, amit most az 1. §-ban ismertetendő okokból kénytelen vagyok közreadni, olyan kényes, hogy amennyire tudom, százegynéhány év óta, mikor ugyanis a kitűnő Franciscus Fontana[8.] úr először látta a Vénusz kísérőjét, ezideig, amikor ezeket írom, a csillagászok és optikusok közül a jelenség egyszerű kifejtésének ez az általam használt módja senkinek sem jutott eszébe, ezt az én módszeremet annyira a leghelyesebbnek tartom, hogy aki ezt figyelmesen elolvassa, az általam elvégzett és leírt kísérleteket megismétli, azt, remélem, teljesen meg fogom győzni, azokat, akik ezt a holdat valamikor látták, de utána többé nem tudták megpillantani, vagy azokat, akik mindeddig hiába keresték azt a legjobb távcsövekkel, valamint mindazokat, akik ezután látni fogják, s mindazok velem együtt ugyanarra a következtetésre fognak jutni. S mivel aki az általános meggyőződéssel szemben valami újat ad ki nyomtatásban, gyakran olyan olvasókat és bírálókat nyer, akik vagy előítéletekkel vannak telve, vagy már előre eldöntötték véleményüket, vagy nincsenek elegendő tudással felvértezve, vagy akiket a finomabb kísérletek elvégzésekor a jártasságuk cserbenhagy, vagy végül akik véleményüket már azelőtt ki szeretik mondani, mielőtt még maguk kipróbálták volna azt, aminek kipróbálására felhívták a figyelmüket, ezért vezettem minden olvasómat a követendő sorrendben.
I. Az általam előadottak igazságát illető ítéletet tartsák függőben mindaddig, amíg a leírtakat mindent, amint illik, teljes figyelemmel elolvasták; nem elég, ha írásomat egyszer elolvassák, hanem javaslom másodszor is újraolvasni; e második olvasáskor, úgy vélem, el fognak tűnni a kétségek, amelyek az első olvasáskor talán támadtak; tudom ugyanis, hogy gyakran megesik, hogy némelyek vonakodnak elolovasni, amit előadtam, vagy túl könnyen ítélnek az elmondottakról. Nekem pedig szokásom néha röviden összefoglalva sok olyasmit, amit csak egyeseknek akarok elárulni, s ami további kifejtést igényelne, fölvázolni néhány vonással, mint pl. van egy ilyen hely 1765-ös Ephemeridesemben[9.], amely első látásra paradoxnak hat, és amit, amennyire tudom, eddig senki sem vett észre.
II. Úgy vélem, senkire sem kell hallgatnom azok közül, akik e bizonyításaim ellen írtak valamit még azelőtt, hogy az itt leírt kísérleteimet azonos körülmények között gondosan maguk is elvégezték volna; ugyanis nem minden kijelentés téves, ami első tekintetre paradoxnak látszik, hanem mindazokban a dolgokban, amelyekben csak kísérlet dönthet, magunknak kell megismételnünk a javasolt kísérleteket, hogy vajon úgy áll-e a dolog, ahogyan írták, és ha úgy találjuk, hogy igen, akkor is meg kell vizsgálni, hogy a kísérlet javasolt módját pontosan betartottuk-e, ha pedig úgy látszik, hogy nem egyeznek a dolgok, ezt nem csak megfontolásokkal, melyek gyakran a helyesen végzett kísérletnek is ellentmondanak, hanem helyesen végzett kísérletekkel kell kimutatni: ezt és nem más módszert enged meg az optika tudománya. Annak tehát, aki azt fontolgatja, hogy az általam itt leírtakkal szemben valamiféle kétségeit leírná, annak először neki kell feküdnie, hogy az általam leírt kísérleteket maga is pontosan, a leírt módon megismételje és kimutassa, hogy vagy hamisak, vagy ha helyesek, akkor ezeknek a holdaknak az esetére nem jól alkalmaztam őket.
III. Szeretném meggyőzni az Olvasókat, amint az könnyen kitűnhetik ebből az írásomból, hogy én lényegében mindent elolvastam, amit eddig a Vénusznak erről a holdjáról közöltek, sőt sok olyasmit is, ami csak kéziratban van meg, de sosem publikálták; amiért is ha bizonyos közleményeket, írásokat, szövegeket és magukat a szerzőket stb. nem említem meg, ebből senki se merészkedjék érvet formálni arra, hogy azt én nem ismerem; mert nem úgy van, hogy nem ismerem azt, amit az emberség és az önmérséklet tanácsol hallgatással mellőzni. Így nem mondok semmit a hírneves de la Caille[10.] úr nekem írt válaszairól, akinek jelen bizonyításaimat régebben titokban megküldtem, melyeket ő teljes mértékben elfogadott, és azonnal előadást is tartott volna róla a párizsi Akadémia ülésén, ha nem kértem volna őt mély hallgatásra. Nem számolok be Montaigne[11.] úr bizonyos kéziratáról, amelyben válaszol arra a régi bizonyításomra, amit de la Caille úr halála után magához vett. Semmit a híres Wargentin[12.] úr írásairól, amelyeket ezzel az anyaggal kapcsolatban adott nekem; a híres Messier[13.] úr írásairól keveset; semmit La Grange[14.] atyánk írásairól, amelyekben biztosított engem, hogy ő ezt a Vénusz-holdat soha nem látta; semmit a kitűnő de Mairan[15.] úr tanulmányáról e tárgyban, semmit a ragyogó berlini de Baudoüin úr német nyelvű jegyzetekkel ellátott tanulmányáról, melyet a híres Reccard úr fordított és adott ki, stb.
IV. Hogy itt általános bizalmat támasszak, mint az 1.§-ban állítom, nem akarom ezen írásommal oly kiváló és híres csillagászok által látott dolgokat, megfigyeléseiket és fejtegetéseiket, valamint kitűnő Akadémiák e holdra vonatkozó bizonyításait akár kétségbe vonni, akár megtámadni; meghagyom az őt illető értékét mások minden észlelésének stb, és csupán azon vagyok, hogy megmutassam: az ugyanezen hold megfigyelésekor magam által látottak és a mások által látott hasonlók nem egyebek, mint takaros optikai csalódások, amelyeket nem könnyű leleplezni vagy megfejteni, hacsak nem az általam megmutatandó módon.
V. Fölteszem tehát, hogy az Olvasó ismeri az Opticát, a Dioptricát és a Catadioptricát[16.], de legalábbis azokat a bizonyításokat, amelyek minden optikai könyvben mindenütt megtalálhatók, mellőzöm, és elfogadom az optikákban bizonyított tételeket; csak azt bocsátom előre, hogy a visszavert sugarak összetett focusának azt a focust nevezem, amely vagy két lencse kombinációjától származik, melyek egyike a másik focusán belül helyezkedik el, vagy olyan lencséktől, amelyek különböző görbületűek; hasonlóképp a visszavert sugaraknak a tárgyat ábrázoló focusának azt a pontot nevezem, amelybe helyezve a szem valamely lencsében világosan látná önmagát, ha ti. a lencse lenne sötét és a szem világos; és amikor ezeknek a focusoknak a távolságáról beszélek, akkor nem kívánom, hogy azt gondolják, hogy e távolságot olyan precízen akarom megjelölni, hogy pontosabban már nem is lehetne. Ha tehát azt mondom: a domború vagy homorú görbület sugarának felénél, vagy átmérője negyedénél, ezen csak azt akarom érteni, hogy körülbelül, vagy közelítőleg annyi, aminthogy úgy látszik, minden optikai kísérlet csak annyi pontosságot kíván meg, amennyi a matematikai pontosságot egyáltalán nem elégítené ki.
A Vénusz 1761. június 6-án észlelendő híres átvonulása a Nap előtt, ha nem csalódom, a serény észlelőknek alkalmat nyújtott a híres Cassini[17.] és Short[18.] úr által valaha látott Vénusz-hold komoly megfigyelésére is. Én magam, aki az általam már 1757-ben látottakat nagyon jól megjegyeztem, figyelmeztetést intéztem a csillagászokhoz az 1760-ban kiadott közleményemben a Vénusz-átvonulás egyedülálló jelenségéről az én Ephemerideseim 1761-re kiadott kötetében, amelyben kijelentem: „A legkiválóbb távcsővel mind a megfigyelés előtti napon, mind magán az átvonulás napján a napkorong igen gyakran megfigyelendő lesz, hogy nem látszik-e valamely más kisebb és szép kerek folt a Vénusznak akár a mozgás irányába eső, akár az ellentétes oldalán, akár a Vénusznál gyorsabban, akár vele egyenlő gyorsan (de nem lassabban) mozogni a napkorongon, mert egy ilyen, a mondott mozgással rendelkező folt a Vénusz holdja kell, hogy legyen, amilyet más körülmények között még soha senki sem vélt látni." Ez a figyelmeztetésem, amelyet Párizsban a leglángolóbb megfigyelők olvastak, gondolom, többeknek alkalmat szolgáltatott arra, hogy távcsövekkel már a Vénusz-átvonulás előtt e hold után kutassanak, amelyet fent idézett utolsó szavaim kétségbe vontak, és ha valaki felfedezné, fölfedezését a tudományos világgal a lehető leggyorsabban közölje.
E leglángolóbb csillagászok közt a kiváló, tudós és híres Baudoüin úr, a csillagászat igen tudós művelője és legnagyobb előmozdítója, a Vénusz-átvonulás alkalmával való használatra készített 25 lábas dioptrikus távcsővel a Vénuszt már 1761 április vége felé észlelni kezdte e hold kedvéért; igaz, hogy ugyanezen észleléshez számára társat válasszon ki, az újonnan kifejlődött Lemovici Mezőgazdasági Akadémia örökös titkárát, Délépine urat kérte fel erre, aki ugyanezen akadémia híres csillagászával, Montaigne úrral folytatott megbeszélésen rávette, hogy a híres Baudoüin úrnak e munkában társként álljon rendelkezésére. És csakugyan (mint alább leírom) a 9 lábas dioptrikus távcsővel, először május 3-án este 9 óra 30 perckor, majd hasonlóképpen május 4-én, 7-én és 11-én, a híres Baudoüin úr valamiféle Vénusz-holdhoz hasonlót látott és észlelt, amit Párizsba Montaigne úr megírt.
Ezek az észlelések pedig, amelyeket a legkitűnőbb párizsi Királyi Tudományos Akadémia szigorú vizsgálatára adtak át, nem viselték el az első (valamiféle optikai csalódástól való félelem miatti) nyilvános és megfellebbezhetetlen ellenőrzést sem; azonban midőn a kitűnő Baudoüin úr felolvasta nagyszerű tanulmányát az Akadémia ülésén, amelyben (figyelembe véve Montaigne úr észleléseit is) helyes csillagászati ismeretek mellett meghatározta e hold mozgási [keringési] periódusát, [pályájának] csomó[vonala] helyét, pályahajlását az ekliptikához[19.], és a máj. 11-én végzett észleléssel együtt megerősítette ugyanezen elméletet, ekkor a kitűnő Baudoüin úrnak az Akadémia jóváhagyását kiérdemlő értekezését és Montaigne úr észleléseit mindenféle optikai csalódástól, amelynek becsúszásától tartani lehetett, mentesnek nyilvánították, amint ez látható Baudoüin úr kinyomtatott tanulmányának végén, amelynek címe Memoire sur la decouverte du satellite de Venus, et sur les nouvelles observations, qui viennent d'être faites à ce sujet, etc.
Miután hát megvolt a hírneves párizsi Akadémiának ez bizonyítása és deklarációja a Vénusz új holdjára vonatkozólag, melynek léte eddig kétséges volt, most viszont már kétségtelennek számított, nem maradt más hátra, mint hogy az egész világ minden csillagászával nyomtatásban közöljék, és felhívják őket, hogy a Vénusz 1761. június 6-i átvonulásakor, amikor is remény volt rá, hogy a Vénuszt követő holdat a napkorong előtt megláthatják, szorgalmasan keressék azt a Nap előtt. Ennélfogva az elsőként, új értekezésben Montaigne úr által azonnal publikált megfigyelést aztán a kitűnő Baudoüin úr tanulmányának kinyomtatott és szétküldött példányai is megerősítették.
E jeles értekezés példányát, amellyel számomra oly fontos levelezését megkezdte, magának az illusztris szerzőnek, Baudoüin úrnak a jóindulatából 1761 június vége felé kaptam meg. Hogy ezt az értekezést mekkora kíváncsisággal fogadtam, könnyen elképzelhetik, akik megértették, hogy - először: én már 1757-től a Vénusz körül gyakran láttam hasonló jelenséget; másodszor: én biztos voltam benne, hogy ezek, amiket láttam, csinos optikai csalódások, olyanfajták, amelyeket alább megmutatok[20.]; harmadszor: én e disszertáció [megismerése] előtt nem kaptam meg Montaigne úr észleléseit, hanem csak hírből értettem meg, hogy Montaigne úr ezen észleléseit olyan bizonyosnak állítják, hogy e hold létezése felől semmiféle kétség nem maradhatott. Ez volt tehát, ami lelkemben oly hatalmas kíváncsiságot keltett e tanulmány olvasása iránt; elolvastam tehát, és újra elolvastam többször, nyílt lélekkel, amint megérdemelte. Összehasonlítottam Montaigne úr észleléseit azzal, amit én magam láttam, valamint a Cassini úr által régen látott hasonlókkal, és összevetettem a Short úr legújabb [észleleteivel] is, s ekkor láttam, hogy az én általam látottak hasonlók ezekhez, márpedig biztos voltam benne, hogy az én észleleteim szép optikai csalódások voltak, nem is nehezen leleplezhetők. Azonnal leírtam, kivonatosan, alább kifejtendő bizonyításomat, valamint azt a módot, amellyel ez az illúzió a szem retináján létrejön, 1761 július 1-jén la Caille úrnak titokban küldött levelemben, két dologra is kérve őt: először hogy ezt a bizonyításomat természetes titokként gondosan őrizze meg, és senki emberfiának meg ne mutassa mindaddig, amíg tőlem a közlésre engedélyt nem kap; másodszor hogy ennek az optikai csalódásnak a magyarázatára őszintén nyissa meg értelmét, hogy azt vajon helyesnek találja-e, vagy nem. Ő pedig mindkét baráti kötelességének eleget tett: először is amennyiben ezt a titkot hét hónapig igen gondosan megőrizvén magával vitte sírjába a halhatatlan De la Caille, akire emlékezni fájdalmas számomra, akit 1762 márciusában számomra és a tudományos világ számára végzetes betegség ragadott el. Másodszor pedig, hogy bizonyításomat nemcsak helyesnek fogadta el, hanem azt az igen híres párizsi Tudományos Akadémiával azonnal közölte volna, ha nem kértem volna titoktartásra, mint azt két nekem adott levélben is tanúsította.
Megtudván, hogy e bensőséges barátom meghalt, e leveleimet és még néhány más, különböző tudomány anyagát érintő titkos levelet illetőleg aggódtam, hogy ne terjeszszék el tudtom nélkül a közönség körében, ezért rögtön írtam más párizsi akadémikus barátaimnak, kérve őket, hogy előbb említett írásaimat De la Caille írásainak örökösétől követelje magának, s kezelje őket titkosan; választ kapván teljesen megnyugodtam a titoktartás felől. Ám nem sokáig lehettem nyugodt, hiszen 1764 márciusában kaptam egy kötetet, melyet a párizsiak küldtek el nekem, és ebben többek között ama titkos írásaim közül, amelyeket D. de la Caille-hez 1761 júliusában a Vénusz holdjáról írtam, több is szerepelt franciára fordítva, Montaigne úr valami válaszával együtt, amit azokra adott; és ebből megértettem, hogy azok a titkos írásaim, bár tudtom nélkül, már közkézen forognak. Ezért aztán megírtam a kitűnő, nagytudású és hírneves Baudoüin úrnak, hogy nézetemet erről a nyomtatásban kiadandó bizonyításomról világosan föltárnám, ha ezt a kitűnő Baudoüin úr (aki a legfőbb oka volt annak, hogy az említett titkos levelekben kimondtam, hogy az a bizonyításom sokáig rejtve maradjon) helyesnek és kívánatosnak tartaná. És íme, megkaptam e legműveltebb, kitűnő úr levelét: nemhogy kívánatosnak mondja említett közleményem megjelenését, hanem még erős biztatására is méltatja, hogy ideáimat, az általam látottakat, kísérleteimet és amaz optikai csalódásra vonatkozó bizonyításaimat közzétegyem, melyek által az igazság végre kiderül, vagy a hold valós létezéséről, vagy pedig arról az optikai csalódásról, amilyet a mondott levelekben kimutattam.
Íme tehát annak oka, hogy ezt a bizonyításomat most közzé akarom tenni. De ez nem az egyetlen ok, mely engem írásra ösztönöz, hanem nagyobbak is vannak, és e nyomós okok közt a legfontosabb, hogy e hold létezése körül kitört vitának (amely a csillagászok között 1645 óta, amikor a híres Franciscus Fontana úr először látta Nápolyban, napjainkig, tehát már százhúsz éve tart) eldöntéséhez világosságot nyújtsak, vagy inkább, amit még jobban szeretnék, véget vessek neki.
S valóban, ha meggondolom magamban, mennyi munkát vállaltak sokan a legkiválóbb csillagászok közül e hold miatt, vagyis hosszas, de hiábavaló észleléseiket, akiknek pedig, e felfedezésre vágyóknak igen drága az idejük; vagy értekezéseiket és számításaikat, melyeket e látott jelenségek fölött végeztek, vagy másokat, amik iránt e hold oly ritka megjelenései miatt kutattak, úgy láttam, igen igazságtalan lennék a közönséggel, ha ideáimat, továbbá amiket láttam, valamint tanulmányaimat még tovább is csöndben háttérbe szorítanám, amelyeket föltárva pedig, mintegy leplet lerántva, rögtön föltárulna e hold történetének egész misztériuma. Elég legyen hát már a kilenc éven át tartó hallgatásból, és abból, hogy egészen eddig a jelenlegi vitának mintegy titkos szemlélőjeként, vagy e művelt szerzők tudnivágyó olvasójaként szerepeljek.
Senki ne gondolja tehát, hogy ebben az írásomban oly kiváló és híres csillagászok által látott jelenségeket, megfigyeléseiket és tanulmányaikat, valamint e hold [létének] előkelő akadémiák általi bizonyításait akár kétségbe akarnám vonni, akár meg akarnám támadni. Inkább általános bizalmat ébresztek azzal, hogy mások minden megfigyelésének, melyeket változatlan bizalommal tekintek végig, meghagyom az értékét, és minden jutalmam s kívánságom azon híres férfiak és akadémiák legbölcsebb ítéletében van, akiktől e holdról ezelőtt megjelent valami. De azon vagyok, hogy megmutassam, hogy amit én e holddal kapcsolatban észleléskor láttam, valamint más csillagászok ehhez igen hasonló észlelései optikai csalódások voltak, és megmutassam az utat, amelyen ezután a csillagászok, ha úgy gondolják, hogy újra efféléket látnak, megállapíthassák, optikai csalódás volt-e vagy valódi holdat láttak.
Hogy tehát rendben végére járjak a dolognak, először be kell számolnom az összes általam ismert észlelésről, amit e holdról különböző csillagászok készítettek, kezdve a híres Dominicus Cassini úrral, egészen a jelen esztendőig; ezután az általam látottakat írom le, majd végül észleléseim módját és bizonyítását teszem hozzá; amit elvégezvén, pártatlanul javaslom, hogy az én észleléseimet más csillagászok is végezzék el, és saját kísérleteikkel kutassák ki a dologban az igazságot.
A következő fejezetekben Hell részletesen leírja az említett szerzők észleléseit, majd a sajátjait is. Ezután nagyon precízen megmutatja, hogy különböző rendszerű távcsövek használata esetén hogyan jöhetnek létre „szellemképek", reflexiók az optikai elemeken.
Ezek után a könyv utolsó fejezetében levonja a következtetéseket az előbb leírtakból. E fejezet egy része ismét tudományos alaposságú fejtegetés, amit nem kívánunk közölni, mert megkívánná a közbülső fejezetek ismeretét, valamint komoly fizikai tudást is. A számunkra érdekes rész inkább a következő.
X. § A Vénusz-illúzió, vagy optikai csalódás
korolláriumai[21.]
Kimondtam már az Intelmekben is, és az I. §-ban is, hogy én annak a Vénusz-holdnak igen kiváló férfiak által végzett megfigyeléseit, amelyeket a II., III., IV., V. és VI. §-ban fölidéztem, meg akarom hagyni a maguk értékében, és ezt az értekezést nem is az okból közlöm, hogy amit ők igazi és létező Vénusz-holdnak mondtak ki, azt én csalódásnak hirdessem ki, és erről a csinos illúzióról, amely bárkit, aki látva látta, tévedésbe tudott ejteni, kimutassam, hogy velük is így tett; tehát legyen bár a hold reális, ahogy ők akarták; akkor is szabadjon nekem azokat a vizsgálatokat itt közölnöm, amelyeket, úgy gondolom, maguknak a fentebb említett megfigyelésekről szóló értekezésem olvasóinak is ajánlatos elvégezniük De ha ezek a bizonyításaim lehetővé tennék, mint remélem, hogy a csillagászati észlelők ettől fogva mindig láthatnának [ilyen] illúziót, ahányszor csak tetszik nekik, amikor is láthatnák, hogy alaposan tévedtek, látva a teljesen igazi holdnak tetsző illúziót, könnyen meggyőződöm arról, amit az ilyen csalódáshoz Phaedrus [sorai] a III. könyv XIII. meséjében hozzáfűznek, vagyis:
A forma egybevág, a szín ugyancsak, így
ez ügyben minden kétely indokolt lehet.[22.]
Legyen tehát szabad azon kiváló férfiak
által látottakat, az ő szerzőségüket
és ítéletüket érintetlenül
hagyva, összevetni az én bizonyításaimmal,
és próbára tenni, hogy vajon bizonyításaimból
levezethetők és megfejthetők-e a II., III.,
IV., V. és VI. paragrafusokban számbavett Vénuszhold-látványok.
I. korollárium. A híres Cassini, amikor 1672-ben és 1686-ban úgy vélte, hogy a Vénusz holdját látja, egy 34 lábas dioptrikus távcsövet[23.] használt, s mivel ebben az öszszefüggésben erről a távcsőről semmi mást nem mond, az nyilván a csillagászati távcsövek rendes módja szerint épült, vagy egyenlően, vagy egyenlőtlenül mindkét oldalán konvex okulárlencsével[24.], és így a látvány a IX. § IV. esetére vezethető vissza, ha pedig az okulárlencse meniszkusz[25.] volt, akkor a látványt a IX. § II. esetére lehet visszavezetni, amely két eset ezt a csalódást oly zavarosnak és kissé homályosnak mutatja, ahogyan magát a jelenséget Cassini úr is zavarosan megjelenőnek mondta, mint a II. §-ban [leírtam]. Ha Cassini távcsövének okulárja több lencséből volt összeállítva (amely konstrukciónak azonban abban a korban aligha volt helye), akkor ha az első lencse meniszkusz volt, akkor azt kell mondanunk, hogy annak a távcsőnek a konstrukciója olyan volt, amely a IX. §-nak vagy az I, vagy a II. esetéhez áll közel: ha viszont az első lencse (a több lencsés esetben) kétszer domború volt, vagy plánkonvex, akkor a távcső konstrukciója a IX. § III. vagy V. esetéhez látszik hasonlónak.
II. korollárium. A híres Short úrnak a III. §-ban leírt észlelései, mint mondják, egy 16 és fél hüvelykes Gregory-rendszerű távcsővel[26.] készültek, amely különböző nagyítású okulárlencsékkel volt fölszerelve; és a holdnak az a képe világos, jól határolt, a Vénusz fázisát követő volt, átmérője a Vénusz átmérőjének kb. egyharmada stb. Mindez azt mutatja, hogy az a látvány a IX. § I. vagy III. esete szerint állt elő, amelyekben a jelenség igen könnyen és világosan jelenik meg, úgyhogy nekem a meniszkusz-okulárral felszerelt Gregory-távcsövekkel [az ilyen kép] hogy úgy mondjam, százával, azaz amennyit csak akartam, igen szépen jelentkezett.
III. korollárium. Montaigne úrnak a IV. §-ban leírt észlelései, mint mondják, egy 9 lábas dioptrikus távcsővel készültek; így hát ha az a távcső a Dollond-rendszer szerint több okulárlencsével volt fölszerelve, melyekben a szemhez legközelebbi lencse meniscus szokott lenni, akkor azok a látványok a IX. § I. esetéhez tartoznak, ha pedig a szemhez legközelebbi lencse kétszer domború volt, akkor a IX. § III. esetéhez, ha viszont Montaigne úr távcsöve a csillagászatban megszokott módon csak egy lencsével volt szerelve, akkor ez a lencse vagy meniszkusz volt, vagy mindkét oldalán, egyenlően vagy különbözőképpen domború, és ekkor a látványokat a IX. § megfelelő esetéből lehet levezetni; ugyanez a helyzet a koppenhágai Roedkier úr távcsövére és az altisodori Montbarron úréra is, amelyeket az V. és VI. §-ban írtam le, ezekre a IX. § alatt általam jelölt osztályok vonatkozhatnak.
Így tehát hogy azok a látványok a IX. § szerint álltak elő, elég világosan látszik; maradtak azonban bizonyos jelentékeny nehézségek, amelyek igen elmés férfiakat is sokat foglalkoztattak, és amelyek, úgy látszik, igen meggyengítik ezt az én módszeremet, amellyel vizsgáltam azon híres észlelők által látott jelenségeket; ezek pedig a következők. Először is: ha ez az optikai csalódás valamely gyakorlott észlelőnek egyszer előállt a IX. § valamely esetében leírtak szerint, akkor ugyanez a csalódás ugyanazon észlelők által hozzáértően keresve a távcsővel, miért nem jelent meg többé? Cassini úr legalábbis kétszeri alkalmon kívül, noha igen gondosan kereste ezt a holdat, soha többé nem látta. Ugyanígy járt Short úr, aki azt egyetlen napon kívül, azután többször nem tudta megpillantani, bár a legkiválóbb körülmények között kereste; úgy látszik tehát, hogy az említett észlelők a fent említett módon valami mást láttak, mint optikai csalódást.
E kérdésre, amely igen nehéz azoknak, akik azt a látványt valódi Vénusz-holdnak tartják, nekem, aki azzal 1764 óta igen gyakran mindenféle módon kísérletezem, igen könnyű felelnem. Hogy hát e nehézséget szép sorjában megoldjam, először is azt kell kérdeznem, hogy vajon azok az észlelők, akik a holdat látták, ugyanazt a távcsövet alkalmazták-e annak keresésére, mint amellyel egyszer látták a holdat, vagy másikat? Ha másokat, mint amellyel egyszer a holdat látták, akkor úgy látszik, azt kell mondani, hogy ezek a távcsövek nem biztosították ugyanazokat a szükséges feltételeket, mint amelyeket azok a távcsövek, amelyekkel a holdat látták, akkor pedig nem csoda, ha ezekkel nem jelentkezett a csalódás, mint ahogy a IX. §-ból levezethető, azaz talán olyan volt a konstrukciójuk, hogy a visszavert sugarak fókuszpontja előbb vagy hátrább esett, mint a megtört sugaraké. Ha viszont ugyanazokat a távcsöveket használták annak további keresésekor, mint amellyel a holdat egyszer látták, akkor még azt is meg kell kérdezni, hogy változatlanul (de valóban változatlanul) használták-e ugyanazt a távcsövet? azaz ugyanaz volt-e az okulár első lencséje? és ugyanúgy helyezkedett is el? és a szemtől is ugyanolyan távol volt, mint amikor a hold feltűnt? és az első fényrekesz, illetve a távcső szem felőli apertúrája is ugyanaz volt-e, avagy kisebb? mert ha ezen feltételek valamelyike más lett a hold észlelése után, mint ami annak észlelésekor volt, akkor nem csoda, ha az [a látvány] nem jelentkezett többé, mint ahogy a IX. § feltételeiből nyilvánvaló. És ha ugyanazon távcsőnek mindezek a tulajdonságai ugyanazok és változatlanok voltak a látvány észlelése után, mint amikor látták a holdat, akkor is hozzá kell tenni, hogy minden egyéb is ezeken kívül azonos volt-e, vagyis: derült ég, páráktól mentes Vénusz, a Vénusztól távoli Hold, a Vénusz holdjának esti szürkület előtt vagy a reggeli szürkület után végzett keresése stb.; szóval ha föltesszük, hogy mindez ugyanaz volt, de ha csak a következő feltételre (amelyet mint igen lényegest, itt hosszabban kellene bemutatnom) nem ügyeltek, akkor megint csak nem lenne csoda, ha azt a holdat ugyanazon, változatlan távcsővel ugyanazon észlelő nem látná többé; ez a feltétel volt az oka, amikor még nem ismertem, és nem ügyeltem rá, hogy én (és velem együtt persze a többi emberek ezrei) színházi látcsővel fentebb a VIII. §-ban kifejtett [módon] a Holdat figyelve százszor is, ama feltétel felismerése előtt sosem láttam a Holdnak holdját, amelyet pedig ma én is, mások is ugyanezzel a távcsővel (csak e feltételre ügyelve) annyiszor látok, ahányszor akarok.
Ez a nagyon alapvető feltétele annak, hogy akárhányszor láthassuk a holdat, vagyis a Vénusz-illúziót ugyanazzal a változatlan távcsővel, amivel egyszer láttuk, a következő: hogy tudniillik a szem igen lassú (de valóban a lehető leglassúbb) mozgással, és nem sietve, és bizonyos szünetekkel helyeztessék pontosan ugyanabba (de valóban ugyanabba) a távolságba az okulárlencsétől, mint amelyben volt, amikor első alkalommal látta a jelenséget. Ez az alapvető feltétel annyira finom, hogy hacsak a szemnek a lencsétől való távolságát nem úgy, mint leírtam, kis szünetekkel és szinte észrevehetetlenül lassú mozgással keressük, akkor a csalódást legföljebb szerencsével láthatjuk meg, de aligha sikerül újra megpillantani. (…)
Observatio transitus Veneris ante discum Solis die 3 junii anno 1769.
Wardoëhusii, auspiciis potentissimi ac clementissimi regis Daniae et Norvegiae,
Christianis VII. facta, et Societati Regiae Scientiarum Hafniensi praelecta a R.P.
Maximiliano Hell, e S.J. astronomo Caesareo-Regio Universitatis Vindoboniensis,
Societatis Regiae Scientiarum Hafniensis, et Nidrosiensis membro, atque Academiae
Regiae Scientiarum Parisinae membro correspondente. (Hafniae, 1770. Typis
Orphanotrophii Regi, excudit Gerhard Giese Salicath.)
Amikor 1767-ben semmire sem gondoltam kevésbé, mint hogy a Vénusznak a Nap korongja előtti, 1769. évben esedékes, sokat emlegetett átvonulásának, amely számomra Bécsben nem látható, megfigyelése kedvéért állomáshelyemet, obszervatóriumomat akár csak egy időre elhagyjam, és ebben megállapodván, elhárítva már két külföldi meghívást is, és belenyugodva, hogy majd más csillagászok által észlelt időpontokból azonnal el fogom végezni napparallaxis-számításaimat, gondtalanul időztem Bécsben; új, legkevésbé sem várt, a tudományok országában érdemek szerzésére született lelkemhez különösen illő meghívás érkezett hozzám Bachoff gróf Őexcellenciájától, Dánia Legkegyesebb Királyának az én Királyom Udvarába [küldött] Császári Követétől[29.], Legkegyesebb Udvarának nevében, hogy a Király költségén és eszközeivel a kiválasztott csillagászok részéről Dániába utazzam az Északi Sarkhoz amaz észlelés céljából, ha van kedvem, [éspedig] Wardoëhusba, ebbe az arktiszi Csillagászati Teátrumba, és ha nekem is úgy tetszik, foglaljam el a vezető tisztségét; így hát elhatároztam magam, hogy amaz észlelés végett nem fogok - mint mondani szokás - körömszakadtig ragaszkodni a Bécsben maradáshoz, mintha valami varázsütésre elgyöngültem volna, s nem sokra becsülve már előrehaladottabb koromat, sem az út nehézségeit, az életveszélyeket, sem pedig testi erőimnek gyöngeségét az arktikus égbolt és légkör kegyetlenségéhez, hanem megkapván az engedélyt az útra legfelségesebb császáromtól és királynőmtől, MÁRIA TERÉZIÁTÓL és a legfelségesebb II. JÓZSEF császártól, rendbe téve dolgaimat a császári és királyi obszervatóriumomban, kiválasztva az útra társamul a Societasomból[30.] a csillagászatban kiválóan jártas férfiút, P. Sajnovicsot, s mikor az útra a legfelségesebb dán Király elegendő költséget nyújtott, s az egész tudományos expedíció terveit bölcsen meghatározta Thott gróf Őexcellenciája, főminiszter, a királyi udvar belső titkos tanácsosa, megrendelve végül a csillagászati műszereket a legtudósabb Horrebow[31.] úrtól, a koppenhágai Obszervatórium messze leghíresebb koppenhágai csillagászától, elégedetten, bátor és rettenthetetlen lélekkel útnak indultunk az Arktisz felé, és Wardoëhusban (túljutva Isten segítségével minden életveszélyen) 1768. október 11-én épen és egészségesen kötöttünk ki. Itt azután hevenyészett, de a csillagászati észlelésekre igen alkalmas obszervatóriumot építvén, és ezt minden reményen felül már december 23-án befejezvén és elkészítvén, megkezdtem csillagászati, fizikai stb. megfigyeléseimet, amelyeket egészen 1769. június Nonae-jáig[32.] naponta, egyetlen alkalmat sem hagyva ki, gondosan folytattam; mint remélem, nem is eredmény nélkül, ahogyan mindezeket a munkákat Expeditio Litteraria c. munkámban világosan ki fogom fejteni[33.]. De addig is nem lesz haszontalan talán áttekinteni e [tervezett] munkám fejezeteinek tartalmát, kihasználva e tudományos expedíció alkalmát, gazdagítva és előmozdítva azokat, akik a tudományok és művészetek művelésére vállalkoznak, amint az alábbi számokban elvégeztem. Leírva tehát mindez a Litteraria Expeditio c. műben olvasható.
Azokat a dolgokat sem hanyagoltuk el, amelyek az állat- és növényvilág, jelesül a kagylók, füvek, algák, zuzmók természetrajzának megvilágításához vagy kiegészítéséhez tartoznak; valamint egyéb, gazdasági alkalmazásukat tekintve igen hasznos megfigyeléseket sem. De ezeket, mivel a Vénusz átvonulásának szóban forgó anyagát legkevésbé sem érintik, csak azért kívántam előrebocsátani, hogy a tudós világ számára nyilvánvalóvá tegyem: ha a mostoha időjárás következtében a Pólushoz küldött más megfigyelőkkel együtt, ama sokat emlegetett észleléssel bezárólag (bár Isten szerencsésen megszerzett jóindulata a Legfelségesebb Király kívánságát mégis méltányolni kívánta) csalatkoznom kellene, e tudományos expedíció a tudományok és a hasznos mesterségek számára mégsem lenne egészen haszontalan és eredménytelen.
Amire mármost a szóban forgó észlelésnek, tudniillik a Vénusz átvonulásának anyagával kapcsolatban fel akartam hívni a csillagászok figyelmét, röviden előadom: Fölépítvén a wardöi obszervatóriumot, aminek leírását majd az Expeditio Litteraria c. munkámban adom, első gondom volt a pólusmagasság meghatározása után, megépíteni ama precíz, a téglafalhoz rögzített gnómont, vagyis csillagászati délvonalat [meridiánt]; a beeső napképet előállító, Bécsben készült fémeszközt hordozó gnómon magassága csaknem hat láb volt, és evvel szemben, tőle kilenc lábnyi távolságban másik függőleges fal épült a napkép felfogására, továbbá a meridiánt jelölő igen vékony selyemszál, amely mellé fehér papírral ügyesen bevont szilárd léc volt erősítve a napkép pontos észleléséhez. A horizontális síkban is a meridiánban kifeszített szál alá ugyanúgy fehér papírral bevont léc volt helyezve; az észlelés idején az obszervatórium ablakszárnyait mind bezártuk, hogy ezáltal a sötétben a napképek pontosabban megfigyelhetők legyenek; egyszóval, semmiről sem feledkeztem meg, ami ennek a gnómonnak a használatát kétségesebbé vagy kevésbé pontossá tehette volna. Hogy azután ez a csillagászati gnómon mekkora hasznomra volt nemcsak két ingaórám ellenőrzésében és beállításában, hanem más csillagászati megfigyelések során is, azt a gyakorlott csillagászok tudni fogják. E gnómon felállításának tehát legfőbb célja az volt, hogy semmit el ne hagyjak, ami nélkül a wardöi égbolt szinte folytonosan változó zordsága miatt a Vénusz átvonulásának megfigyelése eredménytelen maradhatott volna. Hiszen mivel ezeknek és más helyesen elvégzett méréseknek az eredménye a csillagászati óra helyes és pontos ismeretétől függ, ebben a valójában ismeretlen meridián-vonalban a Nap és a megfelelő csillagok alapján kell azt megvizsgálni; de milyen könnyen előfordulhat, hogy sok napig mind az észelés napja előtt, mind akkor, mind pedig az utána következőkön nem készíthető megfelelő megfigyelés, holott pedig a Nap délben igen gyakran fényesen ragyog? Én persze tudom, hogy az egyik vagy másik napmagasságot (ismerve a quadráns helyzetét) az óra jelenlegi állásában számításokkal meg lehet határozni, de mégis előfordulhat, hogy a felhőkkel állandóan fedett égbolt épp csak a [megfigyelendő] kontaktusok pillanataiban tisztul ki, hogy a megfigyelőnek ne maradjon ideje a napmagasság valamelyest pontos megmérésére, különösen e zord éghajlat alatt, ahol a megfigyelő az óra állásában nem lehet hosszú ideig biztos.
A gnómonon kívül felállítottam még két csillagászati ingaórát, amelyek egyike az én sajátom Bécsben, a másikat pedig, amelyet a híres mester, Le Roy[34.] készített, a koppenhágai csillagászati obszervatóriumból vittem magammal; ezeknek az ellenőrzését, beállítását, és a segítségükkel végzett gravitációs, azaz a [nehézségi] gyorsulásra vonatkozó kísérleteket az Expeditio Litteraria számára tartom fenn.
Felállítottam továbbá két, Koppenhágából magammal vitt quadránst, amelyek egyike három láb sugarú volt és aszerint a szabály szerint készítette a leggyakorlottabb mester, Aal úr, amelyet csillagászati művének II. kötete 1827. pontja 149. ábráján leírt az igen hírneves de la Lande úr. A másik mintegy két lábas, amellyel a leghíresebb Niebuhr[35.] úr jóvoltából rendelkeztem, s amellyel ő, a gyakorlott csillagász és geométer, a minapi arábiai útján nagyszámú igen pontos észlelést végzett, én magam ugyanezzel a használatra igen célszerű quadránssal Wardöben is sokat észleltem, az úton pedig minden megfigyelést ezzel végeztem.
Volt több nagyon jó csillagászati távcsövem, amelyek közvetlenül Bécsből való elutazásom előtt, kifejezetten a wardöi használatra készültek; ezeken kívül a legjobban a Koppenhágából való 10 lábas Dollond-féle[36.] achromaticus távcsőnek örültem, bár ennek nem volt mikrométere, ezért ezt is a kontaktusok megfigyelésére használtam. Használtam ezeken kívül más műszereket is, úgymint egy Bécsben készült nagypontosságú fonálmikrométert, két háromlábas, szállal felszerelt távcsövet a meridiánfalon bizonyos állócsillagok kitűzésére, két eszközt a korrespondeálók[37.] használatára, mágnestűket, barométereket, hőmérőket, elektromos gépet az elektromos anyag és a sarki fény közti összefüggés kutatásához, melyet a legkiválóbb de Storm úr Christianiában [Oslóban] osztott meg velem, valamint különféle szerszámokat, mint órás- asztalosszerszámokat stb, amelyeket ezen a minden emberi összeköttetéstől és ipartól félreeső helyen magam szükség esetén használhatok. Így semmit sem hagytam ki, amit csak kívánni lehetett akár ama nevezetes megfigyelés, akár az egész tudományos expedíció szerencsés kimenetele érdekében.
Hátra van még, hogy mindazt világosan kifejtsem, amiről úgy gondolom, hogy a Vénusz-átvonulás megfigyelésének gondosságához és az ennek segítségével meghatározandó napparallaxishoz tartozik, és amiből a csillagászok majd megtudják, mennyi és milyen hitelt adhatnak e munkáimnak. Először meg kell mutatnom a koppenhágai quadráns vizsgálatát, amit követően meghatároztam a wardöi obszervatórium földrajzi szélességét és a légköri refrakciót; majd azt, hogy milyen módszerrel állapítottam meg az obszervatórium szélességét biztosan és kétséget kizáróan, ezután foglalkoznom kell a hosszúságával is, vagyis a különbséggel a wardöi obszervatórium és a kiváló európai obszervatóriumok meridiánjai, tudniillik az angliai greenwichi, a franciaországi párizsi, a dán koppenhágai, az orosz pétervári, a svéd stockholmi, az osztrák bécsi és a német ingolstadti obszervatóriumé közt a június 3-i napfogyatkozás csillagászati észlelése alapján. Tehát mindazt, amit a Vénusz-átvonulás kontaktusainak észlelési módjáról, magáról a Vénusz-átvonulás wardöben végzett észleléséről, továbbá a napfogyatkozás megfigyeléséről és mindenről, ami még ide tartozik, előrebocsátottam, ki kell fejtenem bővebben, világosan, érthetően és a legnyíltabban, amint ez a legfontosabb dolgokban szükséges is.
Az alábbi részt annak megmutatására közöljük, hogy Hell milyen alapossággal készült a nevezetes megfigyelésre, illetve hogy a siker érdekében mekkora körültekintésre volt szükség.
Mielőtt a Vénusz és a Nap szegélyének érintkezésére vonatkozó megfigyeléseket magukat, mielőtt az órák vizsgálatát, illetve az e megfigyelés céljára használt távcsövek felépítését és a többi előkészületet ismertetném, e helyen véltem alkalmasnak előrebocsátani néhány dolgot, amit szerintem hasznos tudni a Vénusz és a Nap szegélyének érintkezése észlelésének módjáról, főként a következő okokból. I. Mivel a csillagászati észlelők között mindeddig nincs definiálva, hogy az észlelt időpontok közül melyiket is akarják a kontaktus [érintkezés] szóval jelölni. II. Mivel a legtöbb észlelő a kontaktusok időpontját, mégpedig mint állítják, az általuk teljesen bizonyosan észlelt időpontját közlik, holott ezeket a legkevésbé sem tarthatjuk az érintkezés valódi időpontjának, hanem vagy későbbiek, vagy pedig előbbiek a helyes időpontnál. Először tehát definiálnunk kell, mit is értsük azon a kifejezésen, hogy valódi észlelt kontaktus; aztán meg kell vizsgálnunk, hogy minden valódi optikai kontaktust lehetséges-e észlelni, azaz hogy szemmel avagy másként meghatározható-e? Pontosan amely szavakkal az általa észlelt - közönségesen optikai kontaktusnak nevezett - időpontokat a megfigyelő alkalmasan és kétértelműség nélkül ki tudja fejezni, azokkal kell is élnie. Nekem ugyanis úgy látszik, hogy a Vénusz belépésekor mind a belső, mind a külső kontaktus szava, ahogyan a különböző észlelők használják, különböző jelentésű és így legalábbis kétértelmű, amit itt bizonyítani is kívánok. Pedig az optikai kontaktus kifejezésről csak úgy szólok, ahogyan azt az észlelő csillagászok használják a Vénusznak a Nap korongja előtti áthaladásának megfigyelésekor, vagy napfogyatkozáskor a Hold áthaladásakor ugyancsak a Nap korongja előtt, illetve a korongnak látszó Vénusz vagy Hold „optikai érintkezésekor" a korongnak látszó Nappal.
Mivel a Nap, Hold vagy a Vénusz gömbje a Föld jelentős távolságából, a Földről szemlélő megfigyelő számára optikailag úgy jelennek meg, mint sík korongok vagy köralakú lapok (*), amelyeknek széleit körök határolják, ezen égitestek optikai kontaktusáról éppúgy kell értekeznünk, mint két fizikai test látszó érintkezéséről: Két körről tehát, akár egyformák, akár különbözők, akkor mondjuk, hogy optikailag kívülről érintkeznek, amikor kerületük egymás mellett optikailag kölcsönösen úgy helyezkedik el, hogy a kerületek egymással szomszédos részei között nincs megkülönböztethető térköz, hanem úgy látszik, hogy egyetlen fizikai pontjuk közös, mégpedig úgy, hogy a megfigyelő egyikük teljes kerületét másikuk teljes kerületén kívül levőnek ítéli. Ha ugyanis egyikük kerületének egy része a másiknak a kerületén belül látszanék, akkor metszőnek, s nem érintőnek mondjuk őket; hogy pedig a megfigyelő ezt megítélhesse, nyilván szükséges, hogy mindkét kör kerületét lássa. Ha ugyanis csak az egyik kör kerületét látná, és a másik kör kerülete számára láthatatlan lenne, akkor miképp ítélhetné meg, hogy azok optikailag annyira szomszédosak, hogy köztük semmi optikai intervallum nem látható? Hiszen senki sem végezheti el két optikailag észlelhető dolog összehasonlítását, ha azoknak csak egyikét látná, a másik pedig a számára egyszerűen láthatatlan. Igy tehát azt állítom, hogy teljesen lehetetlen észlelni a Hold korongjának érzékeinkkel felfogott első külső optikai érintkezését napfogyatkozás kezdetekor, és még inkább a Vénusz korongjának a Napéval való külső érintkezését átvonuláskor. Ilyen érintkezéskor ugyanis a néző sem a Hold korongját, sem a Vénusz korongját, mint amelyek nélkülözik a megvilágítást, és amelyek kívül a Naphoz közel helyezkednek el, nem láthatja meg; ha pedig e korongokat nem láthatja, akkor miként állapíthatná meg, hogy kerületük látszólag annyira közel van a fényes Nap kerületéhez, hogy közéjük nem esik látható intervallum? Az első külső kontaktus pillanatait tehát, azaz az észlelt Vénusz korongjáét a Nap korongjával - teljesen lehetetlen megfigyelni. Azaz: a Vénusz és a Nap gömbjének első külső kontaktusára vonatkozó megfigyelések lehetetlenek.
Ebből már érthető, milyen kétértelműen beszélnek azok az észlelők, akik azt mondják, hogy belépéskor a Vénusz első kontaktusát pontosan ebben vagy abban a pillanatban észlelték. A napkoronggal való első optikai kontaktus ugyanis, mint most igazoltuk, bármely észlelő számára egyszerűen hozzáférhetetlen, mert hogyan fogjuk meglátni azt, ami nem látható?
Ha mármost a megfigyelő az első külső kontaktus időpontjaként azt az időt állapítja meg, amikor a Nap fényes pereme már a Hold vagy a Vénusz sötét korongjának kis részébe belemetsz, vagyis amikor a Hold vagy a Vénusz sötét pereme metszi a Nap fényes peremét, akkor biztos, hogy a valamely előző pillanatban történt első külső optikai kontaktus már elmúlt; de mely pillanatban? ez az, amit egyetlen csillagász sem merészel precízen meghatározni. A napfogyatkozások kezdetének sok megfigyelésében szerzett állandó, úgyszólván napi gyakorlat alapján, a távcső nagyításának ismeretében, valamint a holdperem már bemerült részecskéjéből és annak ismert mozgásából a gyakorlott észlelő körülbelül meg tudja becsülni az elmúlt kontaktus időpontját, ami számára megfigyeléssel egyszerűen lehetetlen; napfogyatkozásoknál a külső kontaktus időpontjának e becslése közepes méretű távcső használata esetén a 10 másodperces határon belül szokott mozogni, nagy távcső esetén pedig 6 vagy 5 másodperc körüli, amint ezt régebben Ephemeridesem 1765-ös kötetében megmutattam.
Mit kell gondolnunk a külső kontaktus időpontjának becsléséről a Vénusznak a napkorong elé való belépése esetén? Kissé előbb már megmutattam, hogy a sötét Vénusz valódi első külső optikai kontaktusát a fényes napkoronggal lehetetlen megfigyelni; amiért is mikor az obszervátor a Vénusz átvonulásakor észreveszi, hogy a Nap fényes szegélyét a sötét Vénusz korongja már kis részben takarja, azaz mikor a megfigyelő számára úgy látszik, hogy a Vénusz kis része már belépett a napkorong elé, az első külső optikai kontaktus biztosan valamennyi idővel előbbre esett; de hát melyik időpontba? Ha a Hold első külső optikai kontaktusa a Nap szélével, mint kevéssel előbb mondottam, 10, de legalább 5 másodpercnyi bizonytalanságot tartalmaz, akkor biztos, hogy a Vénusz elmúlt első külső kontaktusának becsült időpontja 60, de legalább 40 időmásodperc bizonytalanságot kell, hogy tartalmazzon, tudniillik e bizonytalanságok mértéke nagyjából fordítottan arányos a Hold és a Vénusz mozgásának sebességének arányával. Viszont tudjuk, hogy a Hold és a Vénusz mozgásának [szög]sebessége nagyjából úgy aránylik, mint 8 az 1-hez, vagyis mint 5393h : 656h, tehát a Vénusz oly lassú mozgása miatt, amellyel 60 időmásodperc alatt csak 4 szögmásodpercet tesz meg pályáján, az elmúlt külső kontaktus bizonytalanságának 40 és 30 időmásodperc szélső határok között kell mozognia. Hozzájárul még, hogy ez a bizonytalanság még sokkal nagyobbra nőhet a Vénusz kerületének a Holdéhoz viszonyított kicsinysége miatt, ami körülbelül 1:32; és még más körülmények is hozzájárulnak, mint pl. a Nap és a Vénusz szélének remegése [a távcsőben] a látóhatár párái miatt, a szem gyengesége stb. stb, amire tekintettel könnyen érthető, hogy szükségképpen még a leggyakorlottabb megfigyelő is egy percnyi, vagy legalább 50 másodperc körüli hibát követ el.
És ez az igazi oka a Vénusz első külső kontaktusának becsült (nem észlelt, hiszen észlelni lehetetlen) időpontjai erősen eltérő voltának, amelyeket egyazon helyen különböző megfigyelők állítanak. Eltekintve attól, hogy különböző nagyítású és fényerejű távcsöveket használnak, a kevésbé gyakorlottak közül néhányan a megfigyelt kontaktus időpontjaként azt jegyzik föl, amikor a Vénusz valami kis része már belépett a Nap korongja elé. Mások, gyakorlottabbak, a Vénusz mozgásának ismeretéből és a Vénusz Nap előtt látható részecskéjéből megbecsülvén az elmúlt és számukra láthatatlan optikai kontaktus idejét, megadják ezt a korábbi, de általuk csak becsült pillanatot, amiről úgy vélik, hogy az elmúlt és láthatatlan kontaktusnak meg kell felelnie.
Ezen okokból igen helyes, hogy a csillagászok általában törvénynek veszik: a Vénusz belépésének úgynevezett első külső kontaktusának megfigyeléseit a gyakorlatban a napparallaxis meghatározásában felhasználni szigorúan tilos. Ezeket akartam az úgynevezett első külső kontaktusról előrebocsátani, hogy az ilyen észlelésekről alkotott véleményemet nyilvánosságra hozzam. Most röviden előadom, hogyan látom a Vénusz átvonulásakor észlelt első belső kontaktus megfigyeléseinek pontosságát.
Két nem egyforma kör látszólagos belső kontaktusáról, vagyis hogy mikor kerül a kisebb kör a nagyobbikon belülre, akkor mondjuk, hogy bekövetkezett, amikor a kisebb kör kerülete optikailag annyira szomszédossá válik a nagyobbik kör belső kerületével, hogy mindkét kerület épnek látszik, de a kisebb és nagyobb kör kerülete között a fizikailag legközelebbi pontban optikai intervallum (térköz) nem látható. Ha tehát a Vénusznak ez az első belső kontaktusa a Nap kerületével érzékeinkkel felfogható, [akkor] bátor vagyok kijelenteni, hogy véleményem szerint a sötét Vénusz első belső kontaktusa a Nap fényes kerületével alig 15 vagy 10 másodperces szélső határok között nem mondom, hogy megfigyelhető (kicsit később megmutatom ennek fizikai lehetetlenségét), hanem megbecsülhető. Íme a kijelentésemet alátámasztó megfontolások.
Ha a sötét Vénusz belső kontaktusa a Nap korongjára való belépés alkalmával akkor állapítható meg, amikor a sötét Vénusz kerülete úgy kerül összeköttetésbe a fényes Nap belső kerületével, hogy mindkét kerület éppen sértetlennek látszik, azaz legkisebb részük sem hiányos, azonban ugyanakkor a sötét Vénusz kerülete és a vele érintkező fényes napkorong között semmi látható köz nem vehető észre, akkor világos, hogy ez a megállapítás, illetve ez az összehasonlítás szükségképpen helyettesítendő egy másik megállapítással, mégpedig mind a Vénusz, mind a Nap kerületének teljes épségével. Azt kell tehát megnéznünk, hogy a megfigyelő a kerületeknek erről az épségéről megbizonyosodhatik-e legföljebb 10 időmásodpercnyi hibahatáron belül?
Hogy az én véleményem a fényes Nap és a sötét Vénusz kerülete épségének biztos megítéléséről pontosan érthető legyen, legyen a 2. ábrán a távcső látómezeje K, L, M, N. A c, E, G, F kör része jelképezze a napkorong részét, amelynek a távcsőben látható c, P, Q, R része az, ahol a belépő sötét a, c, b, d Vénusz a távcső látómezejének közepére állítva tartózkodik. Akkor nyilvánvaló, hogy a megfigyelő nem állapíthatja meg a Vénusz c szélének a Nap P, c, R szélével a c pontban történő érintkezését, hacsak azt nem ítéli meg, hogy a Vénusznak a kontaktus c pontjából húzott c, d átmérője ugyanakkora, mint a rá merőleges a, b átmérő, vagyis hogy a Vénusz kerületét körnek vehetjük, mert az a, b, c, d Vénusz alakja már pontosan kör, s nem hiányzik belőle a legkisebb rész sem; mint ahogy hiányoznék, ha a Vénusz c, d átmérőjét kisebbnek találnánk, mint az a, b átmérőt. Másrészt a megfigyelő nem állapíthatja meg másképp a Nap P, c, R kerületének épségét, mint hogy megbecsüli, hogy a P, c ív úgy folytatódik-e a c, R ívben, hogy köztük a c pontban már nem látszik törés vagy bevágás. Ezeket leszögezve világossá lesz, hogy mekkora időbeli pontossággal történhetik ennek a belső optikai kontaktusnak a megfigyelése.

Hell rajza a Vénusz átvonulás kontaktusainak
értelmezéséhez
Ha a megfigyelőnek csak szemmértékkel, azaz csak szemmel történő összehasonlítás útján kell megbecsülnie, hogy a Vénusz c, d és a, b átmérője egyforma-e, azaz hogy vajon a Vénusz kerülete már pontosan kör alakú-e, akkor könnyen érthető, hogy a kör alak e megbecsülése bizonyos szükségszerű hibával végezhető csak el, azzal, hogy a Vénusz igen lassú mozgása miatt fizikailag lehetetlen csak puszta szemmel pontosan megítélni azt az időt, amikor a Vénusz c, d átmérője egyenlővé válik az a, b átmérővel, vagy ami ugyanaz, megadni azt az időt, amíg a Vénusz alakja az ép körformát felveszi; és nem könnyebb azt az időt sem meghatározni, amíg a Vénusz c, d átmérője, bár kicsiny, valami csekély résszel még kisebb az a, b átmérőnél. Éppoly könnyen érthető tehát, hogy az obszervátor így nem lehet bizonyos e pontos időadat felől, mint amilyen könnyű a Vénusz kerülete épségének ez összehasonlításában szemmértékkel egy szögmásodpercet tévedni.
Tegyük föl tehát, hogy a leggyakorlottabb megfigyelő legkisebb hibája, amit a Vénusz kerülete épségének szemmértékkel való becslésekor elkövethet, nagyjából 1 szögmásodperces határon belül van, vagyis a Vénusz átmérőjének 1/58 részét tévedhet, amikor azt hiszi, hogy helyesen becsüli egyenlőnek az a, b és a c, d átmérőt; ebben az esetben azt állítom: a megfigyelő a kontaktus pontos idejének meghatározásakor szükségképpen 15 időmásodpercet téved, ennyivel becsüli az optikai kontaktus bekövetkeztét előbbi időpontra, mint amikor az valóban történt, márpedig, mivel a Vénusz a Naphoz képest megfigyelt relatív mozgása során egy időpercben, vagyis 60 másodperc alatt a pályáján 4 szögmásodperccel jut előbbre, nyilvánvaló, hogy 1 szögmásodpercet 15 időmásodperc alatt tesz meg. Mivel tehát az obszervátor szemmértékkel való becsléskor nem tudja a Vénusz kerületének épségét 1 szögmásodpercnél pontosabban megállapítani, tehát nem lehet bizonyos a valódi belső optikai kontaktus bekövetkeztének idejében kb. 15 időmásodpercnél pontosabban. Ha megvizsgálnánk együtt a Nap kerülete épségének vagy a Nap széle P, c és c, R íve folytonosságának puszta szemmel való becslése nehézségét, akkor még sokkal nagyobb hibahatárt adnánk meg a belső optikai kontaktus időpontjának becslésére; és ehhez jönnek még hozzá a megfigyelés egyéb körülményei, mint pl. a Nap közelsége a látóhatárhoz, ami miatt a horizontnál a párák a Nap és a Vénusz szélét rezgésbe hozzák, vagy a közben odakerülő felhők teszik az égitestek szélét kevésbé határozottá és nehezebben megkülönböztethetővé; mit tarthatunk tehát a belső kontaktus ilyen észlelésének pontosságáról, amit a megfigyelők közölnek? és mennyire fognak egyezni több észlelő megfigyelései, még ha ugyanazon helyen, ugyanolyan jó távcsövekkel dolgoznak is? Le kell tehát vonnunk azt a következtetést, hogy ha meg fogjuk kapni a Vénusz mostani belépésekor észlelt belső kontaktust, vagy ha a megfigyelők ennél az észlelésnél a belső kontaktus szóval élnek e kontaktus általuk észlelt időpontjának megadásakor, akkor észleléseik nem lehetnek megbízhatóbbak, mint hogy 15 másodperc szélső hibahatáron, de legalább 10 másodpercen belül essenek. Ezért ha valamely észlelők ilyen módon ugyanazon a helyen észlelvén az első belső kontaktust, szűkebb határon belül, mondjuk 8 vagy 7 másodpercen belül, vagy még inkább ha 4 vagy 3 másodpercen belül egyező eredményeket kapnak, ezt inkább a becslés bizonyára szerencsés voltának, mint a megfigyelés lehető voltának tulajdonítom; sőt azt hiszem, hogy e kontaktus így kapott s majd publikálandó észlelései, amelyeket olyan helyeken készítettek, ahol a Nap a horizont közelében tartózkodott (ilyen helyek pl. Franciaország, Anglia, Spanyolország), sokkal jobban fognak egymástól különbözni, mint 15 másodperccel, talán alig lesznek 50 vagy 40 másodperces intervallumon belül.
Ha azonban a Vénusz belépésének első kontaktusának azt a pillanatot vesszük, amikor észrevesszük, hogy a Nap szélének, mint mondják, egy fényes szála felvillan a Vénusz sötét korongjánál, akkor érthető, hogy ezt a pillanatot sokkal pontosabban lehet megfigyelni, mint a fentebb kifejtett belső optikai kontaktust, s ugyanakkor az is érthető, hogy a pillanat, mikor a Nap e fényes szála felvillan a Vénusz belépése folyamán, nem a belső optikai kontaktus valódi pillanata, hanem későbbi, tehát a valódi optikai kontaktus utáni. Mivel ugyanis a megfigyelő csak abban az időben láthatja a napkorong e fényes szálát, amikor a Nap átmérőjének egy kis részényi Vénusz sötét széle már elmozdult a Nap szélétől, következik, hogy az a pillanat, amikor a Vénusz széle a Nappal optikailag egybeesett, ekkor már elmúlt; azaz az igazi belső optikai kontaktusnak már valamely előbbi időpontban kellett bekövetkeznie.
A kontaktus szó tehát, amelyet az észlelők a Vénusz teljes átvonulásának leírásakor használnak, felettébb kétes, sőt kétértelmű, és kimutattuk a kétértelműséget a külső belépésnél; minthogy egyes obszervátorok szerint a belső kontaktus akkor áll be, amikor a Vénusznak és magának a Napnak a kerülete már kör alakú, míg mások akkor beszélnek kontaktusról, amikor a Nap szélének fényes szálát észlelik magánál a Vénusz sötét szélénél, amely időpontok nyilván egészen különbözők, világos, hogy ha ezek a különböző észlelők ugyanazt a kontaktus szót használják, akkor ez a szó kétes és kétértelmű, nem ismerjük ugyanis észlelésüknek, vagyis a kontaktus meghatározásának módját, tudniillik azt, hogy az első vagy a második értelemben határozták meg a kontaktust. A kontaktus szónak ez a kétértelműsége azután az ugyanazon helyen végzett észlelések között is jelentős eltérésekhez vezethet, sőt kell is vezetnie. Nem csoda tehát, ha az úgynevezett kontaktus észlelései közt még a belépéskori belső kontaktus esetén is 20, 30 vagy 40 másodperces különbségeket találunk.
Mivel a Vénusz első módon észlelt belépéskori belső kontaktusa, úgy látszik, az észlelt időpont biztonsága tekintetében nem lépheti át a 15, vagy legföljebb 10 másodperces határt; viszont a második módon észlelve ugyanazon kontaktus, vagyis amikor a Nap szélének fényes szalagja megjelenik, sokkal szűkebb, 4 vagy 5 másodperc, de van, amikor 3 vagy 2 mp. időhatárok között marad, hiszen az azonos helyen észlelő megfigyelők számára annak a fényes szalagnak a feltűnése ugyanabban az időpontban kell, hogy történjék, tehát mind maguk az észlelések, mind pedig azok, amikről az ezen észlelések számára készített távcsövek teljesítményével kapcsolatban Ephemeridesem 1765. évi kötetében értekeztem, teljesen megcáfolják, hogy úgymond a belépéskor a fényes szalag észlelésében akár csak néhány másodpercnél nagyobb hiba is maradjon, bár ez az időpont későbbi a valódi belső optikai kontaktus időpontjánál, azért igen helyes, hogy a csillagászok általában törvénynek veszik, hogy e nagyon fontos méréseknél, tudniillik a napparallaxis mérésénél nem az első, hanem a második módon észlelt kontaktust használják.
Mindezt, amit a Vénusz belépésének mind külső, mind belső kontaktusáról előrebocsátottam, azzal a céllal akartam mondani, hogy amikor a csillagászok az összes kontaktusra vonatkozó észlelésemet olvassák, megértsék a megfontolást és okot, hogy a Vénusz-átvonuláskor észlelt időpontok előadásakor miért kerülöm következetesen a kétes és kétértelmű kontaktus szót, és e kétes szó helyett inkább az én észlelési módomat írom le világosan és egyértelműen, amiből megértsék, hogy az általam kapott, mind az első, mind a második értelemben vett kontaktust helyesen észleltem; ugyanis úgy gondolom, hogy az ilyen fontos dologban, mint amilyen ez az észlelés, az obszervátornak világos, biztos és egyértelmű szavakkal kell élnie, és semmi nem fölösleges, ami valahogyan hozzájárulhat ahhoz, hogy az ilyen észlelés minden tekintetben megbízható legyen.
De bár a Vénusz belépésére vonatkozó észlelésemben a kétes értelmű kontaktus szót kerülöm, ugyanezen szót használhatónak tartom a Vénusz kilépésének leírásakor. A Vénusz kilépésének megfigyelési módja ugyanis, bár nem az egyetlen, de a legbiztosabb és minden észlelőnél közös; és ez a kontaktus szó a Vénusz kilépésekor akár a külső, akár a belső kontaktusra alkalmazva nem lehet kétes vagy kétértelmű. Hiszen minthogy a Vénusz kilépésekor a belső optikai kontaktust minden észlelő arra a pillanatra teszi, és bizonyára akkor is van, amikor a Vénusz sötét korongja a Nap látható korongján úgy érinti a Nap fényes peremét, hogy a Vénusz sötét szélének részétől többé már nem látszik a nap széléből semmiféle vékony szalag, azaz amikor a Nap szélének vékony szalagja szétválik; e pillanatban nincs többé látszó távolság a Nap és a Vénusz széle közt, és mivel a Nap fényes szélének e kioltódása exact észleléséhez nincs szükség a Nap és a Vénusz kerületének összehasonlítására, vagyis hogy már elvesztették-e kör alakjukat, vagy vajon a Vénusz átmérője egy kis részével még rövidebb-e stb., a kontaktus időpontjának bizonyosságához semmi más bizonytalanság nem járul, mint ami a távcsövek különbözőségéből, az égbolt derült vagy felhős állapotából, a Nap horizont feletti magasságának eltérő voltából származik; és ezért ha az égbolt és az észlelés egyéb körülményei kedvezők, ezt a belső kontaktust szerintem olyan pontosan lehet észlelni, hogy csodálkoznunk kell, ha egyformán jó távcsövekkel ugyanazon a helyen dolgozó észlelők 4 vagy 5 másodperccel eltérő adatokat kapnak. Számomra kedvező égbolt mellett ez a kontaktus annyira pillanatszerűnek tűnt, hogy időpontjában még egyetlen másodpercnyit sem kételkedem.
Ugyanilyen megfontolásból a Vénusz Nap elől való teljes kilépésének időpontját csak egy módon, úgy, ahogy a napfogyatkozások végét, a legbiztosabban, minden csillagász egyformán észlelheti, mivel ez akkor következik be, amikor a Nap kerületének azon a részén, ahol a Vénusz kilép, többé nem látszik bevágás vagy a Vénusz nyoma, azaz amikor a Nap kerülete már teljesen kereknek és határoltnak látszik, és ez az a pillanat és ezt kell a Vénusz kilépéskori külső optikai kontaktusának nevezni. A kontaktus szó tehát a teljes kilépéskor biztosan és kétség nélkül érzékelhető, minden észlelővel közösen. Hogy ez a Vénusz kilépésénél észlelt külső kontaktus még pontosabban megfigyelhető, mint a teljes belépésnél a belső kontaktus, amit a fent részletezett első módon észleltek, az az előbb mondottak szerint külön magyarázat nélkül is érthető.
Ha mármost valaki a Vénusz teljes belépésekor megfigyelt belső kontaktusról fentebb leírtakból azt venné ki, hogy én azt akartam megmutatni, mintha a Vénusz teljes belépésének megfigyelései, amit a csillagászok első belső kontaktusnak neveznek, alkalmatlanok egy oly fontos dolognak, mint a napparallaxisnak a precíz kiszámítására, merthogy az első módon észlelt kontaktus 15 vagy több időmásodpercnyire is pontatlan lehet, és a második módon észlelt kontaktus is túllépheti a 4 vagy 5 időmásodperc hibát, vagyis a Vénusz és a Nap szélének valódi optikai kontaktusa a teljes belépéskor nem figyelhető meg pontosan, azt emlékeztetném arra, amit fentebb már jeleztem: hogy tudniillik a csillagászok azt a törvényt hozták, hogy a parallaxis meghatározására nem használnak más kontaktust, mint a második módon észleltet. Ez a második módon észlelt kontaktus pedig különböző észlelők esetén 4 vagy 5 időmásodpercen belül lehet pontatlan, de általában a hiba nem halad meg 3 vagy 2 másodpercet; a két vagy három időmásodperc pedig, összevetve az egyik belső kontaktustól a másikig tartó teljes átvonulás tartamával, amelyet két különböző helyen levő obszervátor észlelt, amiben a legnagyobb a parallaxis okozta eltérés, az ezekből meghatározandó napparallaxist nem teszi pontatlanabbá, mint a teljes parallaxis egy háromszázad részényire; az ez évi Vénusz-átvonulás észleléséből meghatározandóknak ez a pontossága bizony még mindig nagyobb, ha a déli sarkvidéki megfigyelők szerencsével jártak, mint amekkora lehetett az 1761-es Vénusz-átvonulásnál, hozzávéve még, hogy a különböző, legnagyobb parallaktikus hatást (eltérést) adó helyeken mindkét kontaktust, mégpedig mint Halley[40.] kívánta, egyetlen másodpercnyi pontossággal észlelték; az 1761-es legnagyobb megfigyelhető parallaktikus effektus az átvonulás teljes tartamának időkülönbségére nem volt nagyobb (feltéve, ha a Nap parallaxisa 10"), mint 12 vagy 13 időperc, ebben az évben pedig az északi-sarkon észlelt átvonulás tartama között és aközött, amit remélhetőleg a déli részen, a déli tengeren észleltek, feltéve, hogy a napparallaxis 9", 24 időpercnyi különbséget kell találnunk.
[Id. mű 71. skk. o., az Observatio Transitus Veneris ante discum Solis die 3. Junii c. fejezetből. Ennek nagy része, amit {…} jelek közé zárva közlünk, Pinzger Ferenc S. J. fordítása.]
{…Az ég még nem volt elég tiszta, a Nap mégis a világosabb tájt foglalta el, délről észak felé hajtott igen gyors mozgású felhőcskék szállingóztak, amelyek az északi oldalon nagyon hosszú felhőkben tömörültek össze. Noha jól tudom, hogy az első külső érintés csak egy negyed órával kilenc után áll be, körülbelül kilenc órakor a készen álló tubusokhoz[41.] mentünk a külső érintést várva, mialatt a szolga az óra mellett foglalta el helyét. Minthogy az első külső érintésnek közvetlen megfigyelése, mint előbb jeleztem, lehetetlen és kár vele bajlódni, én a nyolc és fél lábnyi, fonálmikrométerrel ellátott, különben kitűnő, de a másik kettőhöz képest kevésbé jó tubust vettem, nehogy a Nap hasztalan megfigyelésével elfárasszam és elgyöngítsem szememet, amelyet a fölöttébb fontos első belső érintés pontos észlelésére akartam jó karban tartani. P. Sajnovics majdnem éppen olyan jó és annyira nagyító, tíz és fél lábnyi messzelátóval volt fölszerelve, mely ítéletem szerint még valamivel világosabb képet adott, mint a koppenhágai tíz lábnyi achromatikus tubus. Borgrewing[42.] urat az első külső érintés megfigyelésére az achromatikus tubushoz állítottam, amelyet én magam a Nap felső részére (a tubusban az alsóra) irányítottam, ahol a Venus majd belép, és figyelmeztettem, hogy a napkorongnak ezt a részét mindig a tubusban tartsa és mihelyt látja, hogy fekete részecske a Nap szélét mintegy marja és megszakítja, - azonnal kiáltson és az órára figyelő szolgával olvastassa az első és a másodperceket. Ugyanezt ígérte Sajnovics is. Én azalatt nyolc és fél lábnyi tubusommal a Nap mozgását folyton követve és közben-közben beletekintve, ezt a részletet szüntelenül a tubusban tartottam, hogy társaim adta jelre a Venusnak a Napba behatoló részecskéjéből becsléssel meghatározhassam a külső optikai érintkezésnek közvetlenül meg nem figyelhető időpontját. Közben az égnek ez a tája, amelyet a Nap foglalt el, tisztább lett, mert a felhők, mint mondottam, gyorsan észak felé mozogtak.
Amint tehát kilenc óra után tubusaink mellett nyugodtan és hallgatagon vártuk a belépést, először Borgrewing úr achromatikus tubusával a Napra tekintvén, odakiált a szolgának és megolvastatja vele az óra időrészecskéit, mert ő valami feketeséget lát a Nap szélén behatolni, ugyanazt kiáltja néhány másodperc múlva P. Sajnovics, én az adott jelre azonnal megtekintve tubusomat észreveszem, hogy a Venus átmérőjének egy része, amelyet becslés szerint két ívmásodpercnyinek találtam, már belemerült a Napba; ezért úgy okoskodtam: ha a Venus mozgására nézve egy körívnyi másodperc 15 időpercnek felel meg, akkor a közvetlenül meg nem figyelhető első és külső optikai érintés szükségképpen 30 másodperccel előbb állott be:
|
Az időpont, mikor Borgrewing úr és P. Sajnovics
fölkiáltottak, a szolga jelzése szerint a bécsi órán ez volt: | 9h 15' 17" |
| Tehát az igazi, külső optikai és közvetlenül
meg nem figyelhető érintés körülbelül beállott: | 9h 14' 47" |
| Látszólagos magassága a Nap szélének,
amelybe a Venus belépett, volt: | 7° 37' |
Amerre a Nap mozgott, elég tiszta volt az ég, a napfoltokat és a Venust jól meg lehetett különböztetni.
Továbbá mialatt a Venus már majdnem félig belemerült a Napba, mi a teljes belépés megfigyelésére készülődtünk. Én a tíz lábnyi achromatikus, Dollond-féle tubust használtam, P. Sajnovics az előbb említett tíz és fél lábnyit. Borgrewing úr a nyolc és fél lábnyit, amely mikrométerrel volt ellátva. Sima kristályüveget ügyesen elhomályosítva olyformán alkalmaztunk, hogy ugyanazt az üveget minden eshetőségre, akár tiszta, akár borús időben használhassuk. Midőn a teljes belépés már közel volt és a Nap körülbelül egy fokkal lejjebb állott a látóhatárhoz, a Nap széle kissé rezegni kezdett, de oly kis mozgással, hogy a megfigyelés pontosságát szerintem korántsem teszi kétségessé. Tehát a teljes belépést achromatikus tubusommal így figyeltem meg.
|
A Venus széle kerekded formáját - úgy
látszik - már majdnem visszanyeri | 9h 32' 35" | |
| (**) Ítéletem szerint a Venus és a Nap kerületei
már teljesen kerekdedek, de még nem látszik a Nap fényes széle | 9h 32' 42"} | |
| (***) Feltűnik a Nap szélének fényes
fonala, miután a Venus már tejesen belépett | 9h 32' 48" | |
| {. Sajnovics tíz és fél lábnyi tubusával
így találta: Úgy látszik, hogy a Venus teljes kerületét visszanyerte | 9h 32' 30" | |
| A Venus teljes belépése, midőn a Nap fényes
széle látható volt | 9h 32' 45" | |
| Borgrewing úr nyolc és fél lábnyi
tubusával a teljes belépést így találja | 9h 32' 10" | |
| A Nap magassága azon a részen, ahol a Venus belépett,
ez volt: | 6° 33' 0"} | |
| A teljes belépés után ismét összehasonlított órák | 10h 23' 58" | |
| Amikor a hafniai óra jelzett: | 9h 38' 0" | |
| ekkor a bécsi mutatott: | 0h 45' 58" |
{ teljes belépés után bejöttek a vendégek az obszervatóriumba, akik a már teljes Venust gyönyörködve szemlélték a Napon. Én eközben abban a reményben, hogy a Vénusz egyik-másik pozícióját a Nap előtt Fouchy módszerével meghatározom, a már kikészített hafniai quadránshoz fordultam; azonban az a hosszúkás és igen sűrű felhő, mely az égterületet délkelettől délnyugatig már nyolc órától elfedte, mintegy egyhelyben függve a Napnak e felhőhöz közeli részét már-már eltakarta. Most mintegy hét időperccel a teljes belépés után a Nap, mozgása során ezt a felhőt elérve, a mi nézőpontunkból a Vénusszal együtt eltűnt; úgyhogy nekem a Vénusz pozíciójának Fouchy[43.] módszerével történő megmérésére egyáltalán nem maradt időm. És mivel az ég egészen fedett volt az átvonulás teljes ideje alatt, egyetlen biztos pozíciót sem lehetett meghatározni 10 órától egészen reggeli két óráig az alábbi okokból: Mivel ebben az időben (ami a ferde körök ismerői számára világos) a Nap az északi meridiánhoz közeledvén, magasságát alig 10 percnyit változtathatta negyed óra alatt, így a Fouchy-féle módszer, amely a Nap gyors magasság-változását kívánja meg, Wardöben ekkor egyáltalán nem volt alkalmazható. A Vénusz korongjának a napkorong legközelebbi szélétől való távolságának mikrométerrel való meghatározását a Nap és a Vénusz korongjának - különösen az átvonulás közepe idején, amikor a Nap alig tartózkodott 3 fokkal a horizont felett - a horizont párái okozta igen erős remegése és fodrozódása úgyis lehetetlenné tette volna. Így tehát semmi haszon sem következett volna e megfigyelés szempontjából, ha az ég derült maradt volna a belépés után, egészen reggeli két óráig, messze az együttállás utánig, ezen a nagyon magas szélességi körön uralkodó viszonyok között; s ez okokból megértettük, hogy az a körülmény, miszerint ama sűrű felhő a belépés után elfedte a Napot, megfigyelésünk hasznosságát és teljességét miben sem akadályozza, hacsak a kilépéskori belső kontaktust szerencsésen megfigyelhetjük. Ugyanis e két időpontot, tudniillik a teljes belépés-, valamint kilépéskori belső kontaktus idejét megfigyelve e tudományos expedíciónk célját is elértük, s a Legfelségesebb Királynak tett ígéretünket is beváltottuk. Sőt e két megfigyelt időpont alapján a Vénusz mozgásának minden elmélete sokkal precízebben kiszámítható, ezeket el nem érve pedig akármilyen pontos mérésekből és pozíciókból aligha lehetett volna meghatározni ugyanezt, mint az ismeretes a gyakorlott csillagászok előtt.
Az ég északi részét mintegy fixen beborító említett felhő a Napot 9 óra 40 perctől reggeli 3 óráig lényegében teljesen eltakarta, s ez annyira általános volt, hogy a hasonlóan északi megfigyelőhelyeken tartózkodó többi megfigyelőt megfosztotta a kontaktusok megfigyelésétől, és tőlem is annyira elvette a kilépés megfigyelésének reményét, hogy azt hittem, már megsirathatom expedícióm szerencsés kimenetelét, hacsak a reményt nem Isten különleges kegyességébe vetjük, akinek e munkát megáldó jóakaratú kezét nyilvánvalóan megláttuk magunk is és a megfigyelésnél jelen volt összes vendég, ahogy ama rémítő felhőt a kilépés megfigyelésekor helyéből elzavarta. Ugyanis körülbelül reggeli 3 órakor, amikor mindenki elvesztette reményét, és a Nap mélyen e felhőbe merült, váratlanul könnyű délnyugati szél támadt, amely elmozdította a felhőt a helyéről és északkelet felé hajtotta az északnyugat felé mozgó Nap elől, amitől is az én igen szomorú és mályen a búbánatba merült lelkem mintegy újra kezdett éledni, és a kilépés szerencsés észlelése miatti örömmel kezdett eltelni, ami pedig soká nem volt remélhető; alig negyed óra telt el ugyanis, midőn a Napot a felhőből a mindenfelé teljesen derült égen (mivel ezen a felhőn kívül, amely északon foglalt helyet, az ég többi helyén a legkisebb felhőcske sem volt) kiemelkedni láttuk; akkor a Vénusz a napkorong szélétől már csak saját teljes átmérőjénél [valamivel] messzebb volt, vagyis több mint negyed órával a belső kontaktus előtt. Így hát a beállított távcsövekkel figyelni kezdtük a Napot a Vénusszal együtt. A Nap annyira világosan látszott, hogy legkisebb foltjait soha ezelőtt ilyen pontosan nem láttam, a Vénusz is oly pontosan és jól határoltan volt megfigyelhető, hogy ennél szebbet nem is kívánhattam; továbbá a Nap és a Vénusz korongja a lehető legnyugodtabb volt, a legkisebb fodrozódás nélkül, hiszen a Nap ekkor már 9 fok 30 perc magasságban, tehát a horizonti párák fölött járt, és az az előbb említett könnyű szellő is megszűnt időközben s a légkör teljesen nyugodt lett. Így tehát a lehető legkedvezőbb körülmények között állapítottam meg akromatikus távcsövemmel a következő időpontokat.
| Amint a Venus széle a Nap széléhez közeledik, látom a | Idő az órán |
| fekete csepp[44.] képződését
a Venus sötét korongja és a Nap széle között | 15h 26' 6" |
| Látom a csepp észrevehető kisebbedését | 15h 26' 12" |
| Ez a csepp hirtelenül eltűnik és mintegy eloszlik,
a Nap és a Venus szélei egybefolynak, eszerint tehát a belső optikai érintkezés beáll | 15h 26' 17" |
| P. Sajnovics tíz és fél lábnyi tubusával
megállapította a biztos belső érintést | 15h 26' 18" |
| Borgrewing úr nyolc és fél lábnyi
tubusával így találta a belső érintést | 15h 26' 10" |
| Ahol a Venus átvonult, a Nap szélének
látszólagos magassága volt | 9°43' |
Ezt a belső érintést oly pontosan láttam, hogy még a másodpercekben sem kételkedem; P. Sajnovics azt állította, hogy ő is észrevette azt a fekete cseppet, amelyet az érintés előtt láttam.
Miután ezt a belső érintést oly szerencsésen megkaptuk, a már félig kilépő Venust megmutattam a jelenlevő vendégeknek, hogy kíváncsiságuknak eleget tegyek; mind magasztalták a Nap és Venus igen tiszta képét.
Midőn a Venus már a teljes kilépés felé sietett, mi ismét a tubusokhoz állottunk és a teljes kilépést ily módon jegyeztük föl.
| Idő az órán | |
| Én achromatikus tubusommal a kétes érintést észleltem | 15h 44' 22" |
| Biztos érintés | 15h 44' 26" |
| P. Sajnovics tíz és fél lábnyi tubusa szerint biztos kilépés | 15h 44' 27" |
| Borgrewing nyolc és fél lábnyi tubusa szerint biztos érintés | 15h 44' 20" |
| Ahol a Venus kilépett, a Nap szélének látszólagos magassága: | 10 4' 0"} |
| Ezután az újra összehasonlított órák | |
| Amikor a hafniai mutatott | 16h 33' 23" |
| A bécsi jelzett | 15h 47' 0" |
| A különbség | 0h 46' 23" |
{A sikerek szerencsés elérése után a vendégek gratuláltak nekünk, hogy Isten a király kívánságát miden reményen fölül kegyesen teljesítette, és én tele örömmel és vigasztalással ennek a sikeres megfigyelésnek szemtanúit barátságosan elbocsátottam.
Mielőtt az észlelt adatokat táblázatba csoportosítom és az igaz időre redukálva közlöm, jó lesz még a következőket is megjegyezni.
Először: Nehogy a számláló és a perceket esetleg hibásan jelző szolga gondatlansága miatt kétségessé váljon az észlelés, úgy magam az órához nagyon közel állva, valamint P. Sajnovics és Borgrewing úr az időpontok jelzése után külön-külön megnéztük az órát, vajon megegyeznek-e a szolga időjelzései a mi jegyzeteinkkel.
Másodszor: Mindegyik közülünk észlelt adatait külön-külön papírra vetette, anélkül, hogy egymással jelekkel vagy szóval közlekedtek volna, míg a cédulákat nekem átadták.…}
Az új csillagképeket, amelyeket az. I, II. és III. táblámon alak és nagyság szerint Fortin[47.] úr kisebb térképének lapjain külön-külön javasoltam, ezen a IV. táblán egy tekintetre láthatóan állítom össze, hogy a csillagászok megértsék e csillagképek helyének és fekvésének alkalmasságára vonatkozó megfontolásokat, melyek által indíttatva legyenek ezeket az én csillagképeimet megítélni és elfogadni, és (ha fehér kövecskékkel mellette szavazván elfogadnák őket), a csillagtérképre rávezetni.
Először is tehát mindez a három csillagkép egymáshoz közel van, az égbolt északi félgömbjének legismertebb és legragyogóbb részére helyezve; hiszen a csillagos égbolt soha nem mutatkozik szebbnek és ragyogóbbnak, mint amikor az Ikrek, az Orion, a Bika és a Nagy Kutya (igen sok első, másod- és harmadrendű csillaggal fenségesen földíszítve) a horizont fölé fölkelvén látható[48.]. - Amikor tehát a mondott csillagképek, derült éjszakán, az égbolt közepén ragyogva látszanak, akkor egyúttal a „Herschel[49.] nagyobb távcsöve" az Ikrek feje fölött, a „Kisebb távcső" az Orion fölött, a Bika feje alatt az Aldebaran csillaga és a Hyadok mellett, valamint a „III. György lantja" az Orion, a Bika, a Cet és az Eridanus között szintén együtt fénylenek ragyogóan az égen, és egy tekintettel, mintegy közös képen (úgy, ahogyan a IV. táblán le vannak rajzolva) megtekinthetők; tehát ezek az új csillagképek nincsenek úgy szétszórva az ég különböző részein, hogy egyikük a tavaszi, másik a nyári, őszi vagy téli égbolton elhelyezkedvén, keresgélni kellene őket a nemtelenebb csillagképek közt, hanem ha az Ikrek csillagképe teljes egészében fölkelvén látható, akkor a Nagyobb távcső, a Kisebb távcső és a György lantja is felkelt és látható az égen; és mind egyszerre láthatók a horizont fölött ragyogni az éjszaka óráiban mindaddig, míg a Cet fejének csillagai le nem nyugszanak, vagy a Nap sugaraiba merülve el nem tűnnek.
Másodszor: Ezen új csillagképek fekvésének alkalmasságát ajánlja még az új, Herschel által észlelt bolygó[50.] helye is, amely e „Herschel távcsövei" között középen tartózkodik, mint a IV. tábla mutatja, amely helyzet azonnal emlékezetünkbe idézi amaz emlékezetes megfigyelést, melyet Herschel az ő távcsövével végzett. És mivel a György Lantja mindjárt e távcsövek alatt látszik nyugat felé ragyogni, emlékezetbe idézi egyúttal III. Györgynek, anglia királyának Herschel iránt tanúsított jótékonyságát és bőkezűségét is, valamint e király nagy érdemeit a csillagászat, a földrajz, a hajózás és általában a természettudományok előmozdítása, gyarapítása terén; és e kegyes jelkép, a György lantja által ajánlja a jövő csillagászainak, örök hálával, az ő egyedülálló vallásossága iránti nyilvánvaló és keresztényi féltékenységet.
Harmadszor és végül meg kell fontolni azt is, hogy a Herschel kisebbik távcsövének csillagai mind állatöviek, szélességük[51.] nem érvén el a 8 fokot, miáltal gyakran fogják használni őket a holdnak e csillagokkal való találkozásai alkalmával, illetve a Nap és a Hold, melyek e csillagokkal párhuzamosan mozognak, hasonlóképpen a többi bolygó helyének meghatározásakor, melyeknek szélessége nem éri el a 8 fokot. - A György Lantjának legtöbb csillaga pedig egyenlítői, vagy legalábbis közel esik az égi egyenlítőhöz, miáltal a gyakorlati csillagászatban, a Nap pályájához, amely e csillagokkal párhuzamos, aztán a műszerek vizsgálatához és azok helyesbítéséhez és korrekciójához igen alkalmasak, és ezért a csillagászok könyveiben a Herschel Távcsövei és a György Lantja nevek igen gyakran lesznek olvashatók.
Remélem tehát s azzal hízelgek magamnak, hogy ez a IV. táblán egyetlen pillantással átlátható két égi emlékmű, először Anglia legfényesebb királyáé, III. Györgyé, másodszor Herschelé, az új Urania bolygó fölfedezőjéé, melyeket magam mint csillagász ajánlottam, a csillagászat egész Köztársaságának[52.] csillagászai által jóvá fognak hagyatni és elfogadtatnak, kölönösen a kitűnő francia csillagászok által, akiknek szavazatával s az enyémmel Herschel kitűnőségét örökre az égre kívánva (a Herschel név helyett, amelyet az új bolygónak de la Lande[53.] úr adott a csillagászati szokás ellenére) Herschelnek ez égi távcsövei által, azt gondolom, eleget tettem, és egyben bebizonyítom azt a bizonyos jövendölésemet (három évvel ezelőtt az én „Lis Astronomorum de Nomine" [A csillagászok közti viszály a névről] c. könyvemben tettem közzé), hogy:
HERSCHEL, míg lesz Föld, míg lesznek csillagok, él
majd,
csaknem mint Newton, nagy tudománya miatt,[54.]
és azt is, amelyet ugyanazon könyvemben III. György angol királyról
mondtam:
Illik, mint tudjuk, tisztelni az égi Királyt, ki
támogatá HERSCHELT, és tudománya müvét;[55.]
ÉS MINDEZ LEGYEN
ISTEN NAGYOBB DICSŐSÉGÉRE[56.].
Általam mondatott a csillagászat köztársasága számára.

 |
Természettudományi és tudománytörténeti dokumentumok |