Lévay
Ákos Vaclav
Vitek Tichy
Géza Bevezetés A fém/kerámia határfelületek számos modern anyagban jelen vannak: kompozitokban, védorétegekben, kerámia szubsztrátra felvitt vékony fémrétegekben. Ezeknek az anyagoknak a mechanikai tulajdonságait határfelüleletek igen gyakran alapvetoen meghatározzák[1-5]. Fontos tulajdonság, hogy a határfelületen hogyan egyenlítodik ki a fém és kerámia alkotók közötti rácsállandó-különbség(miszfit). Ha a fémvastagság egy kritikus értéknél nagyobb, a felületen úgynevezett miszfit-diszlokációk jelennek meg [6-10]. Ezek a diszlokációk nem tekinthetoek rácshibának, hiszen megjelenésükkel csökkentik a konfiguráció energiáját, így e diszlokációk a felületi struktúra alapveto elemei. Általában a fémben, a felületen, vagy ahhoz nagyon közel helyezkednek el[11-13]. Ha a miszfit diszlokációk eleget tesznek a Frank-Bilby formulával[14,15] leírt geometria feltételeknek, a fellépo miszfitet teljes mértékben kompenzálják. Azonban csupán a geometriából nem vezetheto le, hogy milyen miszfit diszlokációk jelennek meg a felületen, hanem a felületi kötések, energiaviszonyok tüzetes vizsgálatára is szükség van. Hagyományos transzmissziós elektronmikroszkópiával (TEM) és nagyfelbontású elektronmikroszkópiával (HREM) számos rendszerben figyeltek meg miszfit díszlokációkat[3,4,16-27]. Az eredményeket geometriailag analizálták, és megállapították, hogy kialakult miszfit diszlokáció rendszer teljes mértékben kompenzálja-e a periodicitások különbözoségét. Ahhoz, hogy a megfigyelt struktúrák és a adhézió erossége közötti kapcsolatot meghatározzuk, elméleti, atomisztikus szintu modellszámításokra és így a felületi kölcsönhatások atomi szintu leírására van szükség. Fém kerámia határfelületek esetében ez okozza a fo problémát (Lásd. pl. [28,29]). Elektronszerkezeti, ab initio számolások természetesen végezhetoek[30-33], azonban e számolások csak kis atomszámnál használhatóak, így csupán a felületek koherens részének vizsgálatára alkalmasak. Valamennyivel egyszerubb modellek is felmerültek,(pl. a tükörtöltés modell [29,34-36]), de alkalmazásuk e rendszerek teljes méretére még mindig nehezen kivitelezheto. Olyan fém/fém felületekre, ahol a kölcsönhatás egyszeru potenciállal, például "embedded atom" modellel leírható, minden részletre kiterjedo atomisztikus számolásokat is végeztek[37-40], meghatározva a felületi diszlokáció struktúrát és az atomi szerkezetet. Nemrégiben hasonló, nagyon egyszeru, párpotenciálokat használó modellszámításokat végeztek[26,41,42] fém/kerámia határfelületre is. Ezen egyszerusített számolásoknak a célja nem a kötés energetikájának a pontos leírása, hanem az adhézió erosségének és a diszlokációk magszerkezete közötti kapcsolat megtalálása. Ebben a cikkben a legutóbb említett megközelítésben vizsgáljuk a (0001)||(111) Al2O3||Nb határfelülelet. Ezen a felületen számos elektronmikroszkópiai vizsgálatot végeztek [16,25,27,43], melyek alapján megállapították, hogy az <1,1,-1> díszlokációknak egy trianguláris hálózata alakul ki, amely teljes egészében kompenzálja a felületi periódus különbségeket. Megmutatjuk, hogy a felületi atomi kötéserosség határozza meg a kialakuló díszlokáció-struktúra szerkezetét éppúgy, mint a diszlokációk magszerkezetét. Megmutatjuk, hogy a kialakuló diszlokáció struktúra létrejöttéhez esetenként anyagtranszportra is szükség lehet. Az atomi kalkulációk eredményét felhasználjuk a kapcsolódó HRTEM felvételek vizsgálatához, elsosorban a diszlokációk keresztezodési pontjainak a hatását a felvételen megjeleno magszerkezetekre, valamint összehasonlítjuk az (0001)||(111) Al2O3||Nb határfelülethez elérheto HRTEM felvételeivel. Geometria Vizsgálatunk tárgyát a (0001)||(111) Zafír || Nióbium határfelület képezi, abban az orientációban, amikor is a Nióbium [111], [1,0,-1] és [1,-2,1] irányai párhuzamosak a Zafír [0001], [2,-1,-1,0] és [0,1,-1,0] irányaival (Lásd [43] 2. és 4. ábráját). Mindkét anyag felülettel párhuzamos síkjai háromfogású szimmetriával rendelkeznek, a fémet választva referenciául a rácsállandó eltérés a 1.9% minden irányban.
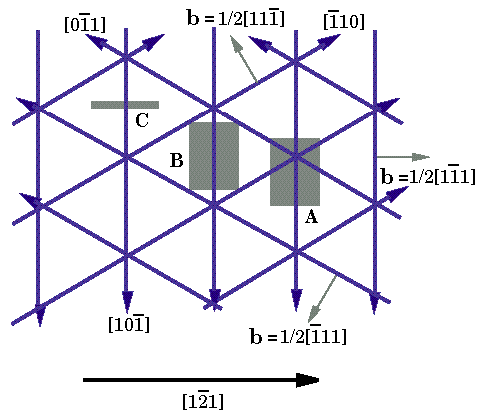
1. Ábra A (0001)||(111) Zafír- Nióbium határfelületen megjeleno három-szögszerkezetu diszlokáció-hálózat sematikus diagramja. Az árnyékolt területek a HREM képszimulációhoz használt mintaterületeket jelölik. Elektronmikroszkópos vizsgálatok[16,17,24,43,44] a felület igen fontos tulajdonságára vetítettek fényt: Azokban a régiókban, ahol a két anyag igen jól illeszkedik (koherens régiók), bizonyos kristálysíkok igen jó közelítéssel törés nélkül folytatódnak az egyik anyagból a másikba. Például a Nióbium (101) és (020) síkjai az alumíniumoxid (0,-1,1,4) és (0,1,-1,2) síkjaiként folytatódnak. Mivel a zafír hexagonális szerkezetében a c/a hányados nem ideális, az említett két sík nem meroleges egymásra, ezért a csatlakozó Nióbium síkokkal egy kicsi szöget zárnak be. (Részletes lásd [14]). További elektronmikroszkópos vizsgálatokkal határozták meg a felületen kialakuló miszfit diszlokáció hálózat elrendezodését (1. ábra): Az 1/2<1,1,-1> Burgers vektorú diszlokációk tiszta éldiszlokációként a három <-1,1,0> irányban elhelyezkedve háromszögszerkezetet alkotnak. A párhuzamos diszlokációk szeparációja 20+/-4 nm. Ezt a szerkezetet a Frank-Bilby formulával[14,15] összevetve megállapítható, hogy azt kielégíti, így a rácsállandó különbséget a miszfit diszlokációk teljes mértékben kompenzálják. Számolási módszerek Jelen tanulmányban ugyanazt az egyszeru módszert alkalmazzuk, amit korábban sikeresen használtak hasonló rendszerekre[41,42]. Ahelyett, hogy a zafír szerkezetét minden részletre kiterjedoen modelleznénk, egy egyszeru tércentrált köbös szerkezettel helyettesítjük. A helyettesíto struktúra pontos orientációját az elozo fejezetben említett szoros geometria kapcsolatnak megfeleloen alkotjuk meg. Jelen esetben ez azt jelenti, hogy a felületet mindkét anyagban ugyanaz a kristálysík alkotja. A kerámiát reprezentáló szubsztrát struktúrájában egy egyenletes deformációt vezetünk be úgy, hogy rácsállandó különbség megfeleljen a zafír/Nb rendszerben vett rácsállandó különbségnek. Az így elkészített modell megorzi a felületi szimmetriákat miközben az atomi szerkezetet jelentosen egyszerusíti. Az atomok egy téglalap alakú cellában foglalnak helyet, periodikus határfeltételekkel, míg a meroleges irányban, megfeleloen távol a relaxált tartományhoz relaxálatlan szerkezetu anyagot csatolunk. Téglalap élei a fémben a [1,0,-1], [1,-2,1] és [1,1,1] irányúak. A felületre meroleges irányban szükséges méretnek összemérhetonek kell lennie a téglalap többi élének a nagyságával.
2. ábra Az atomi számolásokban alkalmazott fém és szubsztrátszerkezet Ezt a modellt különbözo mértéku rácsállandó különbségekre is lehet alkalmazni. Az induló konfigurációt mutatja az 2. ábra 10%-os miszfitre. A modellben szereplo atomok száma a miszfit reciprokának harmadik hatványával növekszik, így sajnos a valódi, mintegy 2%-os miszfit mellett a számolások nem kivitelezhetoek. Számolásokat végeztünk 10%-os, 6.66%-os és 4% os miszfitre. A különbözo értékekre végzett számolások eredményei nagyon hasonlóak, szinte teljes mértékben egymásra skálázhatóak, természetesen egyre több részletet mutatva, így az várható, hogy az eredmények érvényesek a 2%-os esetre is. Minden ebben a cikkben említett eredmény a 4% os miszfit felhasználásával született. Az induló struktúrára egy energia minimalizációs algoritmust alkalmazunk zero homérsékleten és normál nyomás mellett (Lásd pl. [45]), a Nióbiumra számolt energia minimalizálásra. A minimalizáció során a kerámiát reprezentáló b.c.c. szerkezetu szubsztrát atomjait nem mozdítjuk el. Az energiát az atomi kölcsönhatások figyelembevételével az alábbi módon számoljuk: A nióbium atomok között egy Finnis-Sinclair típusú [46,47] centrális soktest potenciált alkalmazunk, A szubsztrát és a Nióbium közötti kölcsönhatást egy párpotenciállal, VMS(r) –sel írjuk le, úgy hogy az képes legyen különbözo kötéserosségeket is leírni (Részletesen lásd [41]). A felületi kohéziós energiát a
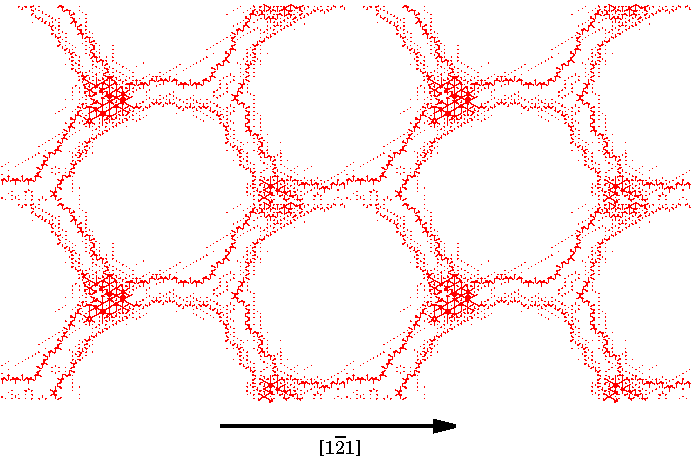
képlet alapján számoljuk, ahol az i szerinti összegzés az összes fématomra, a k szerinti összegzés pedig a szubsztrát atomokra terjed ki; Rik a fém és szubsztrát atom közötti távolság, Ei az Nb atom energiája, míg ESi az ugyanerre az atomra számolt energia relaxált szabad felület mellett. Mivel a szubsztrát energiáját nem számoljuk, nincs szükség a szubsztráton belüli atomok közötti kölcsönhatás leírására. A kötéserosséget az R = EI / E(111) paraméterrel karakterizáljuk, ahol E(111) a tiszta Nióbiumban vett (111) belso felület kohéziós energiája, ami pontosan kétszer akkora, mint a szabad (111) felület energiája. Számolások Két különbözo kötéserosség mellett (R = 0.34 és R = 0.18 -nak megfeleloen) végzett számolás eredményét mutatja be a 3/a és 3/b ábra. Ezen ábrákon a felülettol számított harmadik Nb rétegben , a szomszédos atomok között a relaxáció során fellépo relatív elmozdulások felületre meroleges komponensét ábrázoltuk. Az egyes nyilak hossza arányos a relatív elmozdulással, míg az iránya a vonatkozó két atomot jelöli. Az ábráról így lényegében a deformációmezo felületre meroleges komponensét olvashatjuk le. A diszlokáció vonalában a deformáció nagyobb, a vonal környezetében a nyilak hosszabbak.
(b) 3. ábra A felülethez közeli Nb rétegekben a relaxáció során fellépett deformácio.
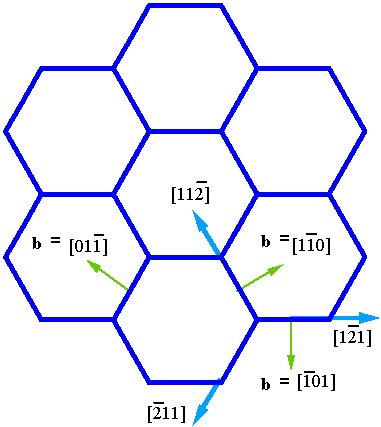
Jól látható, hogy a kialakuló deformációmezo mindkét esetben háromfogású szimmetriát mutat, de a ketto egymástól lényegesen különbözik. A 3/a ábrán megjeleno diszlokáció hálózat hexagonális, az élek a [1,-2,1], [1,1,-2] és [-2,1,1] irányúak. E hálózat sematikus ábráját mutatja a 4-es ábra. A Frank-Bilby formulának megfelelo Burgers vektoroknak [1,-1,0], [-1,1,0] és [0,-1,1]-nek kell lenniük. Ugyanakkor a 3/b ábrán megjeleno diszlokáció struktúra módosított háromszög-szerkezetet mutat (világosan látható a két különbözo háromszög elem). A diszlokációk az [1,0,-1], [-1,1,0] és [0,-1,1] irányúak, az 1. ábrának megfeleloen.
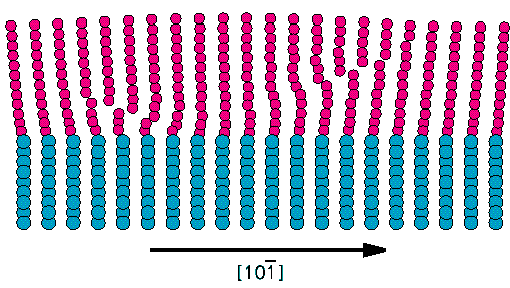
4. ábra A (0001)||(111) Zafír-Nióbium határfelületen megjeleno hexagonális diszlokáció hálózat sematikus diagramja. A két szerkezetet alkotó diszlokációk magjának atomi szerkezetét mutatja az 5/a és 5/b ábra. Az díszlokációkra merolegesen vett ábrák jól mutatják az egyes burgers vektorokat: [1,0,-1] típusú a hexagonális szerkezetnél, és 1/2[1,-1,1] típusú a módosított háromszög-szerkezetnél. A Nb atomokat és a szubsztrátot jelképezo atomokat a 2. ábrának megfeleloen jelöltük. Az 5/a. ábrán két (1,-2,1) síkot; az 5/b ábrán két (10-1) síkot ábrázoltunk a diszlokációk keresztezodési pontjaitól távol. Fontos látnunk, hogy míg az 5/b ábrán, az 1/2[1,-1,1] diszlokáció közvetlenül a határfelületen helyezkedik el, addig az [1,0,-1] diszlokáció az 5/a. ábrán az [1,0,-1] = 1/2[1,1,-1] + 1/2[1,-1,-1] reakciónak megfeleloen felhasadt, és a rész-díszlokációk a felülettol 3-8 réteg mélységig eltávolodtak, E felhasadás az (123) és (321) síkok mentén, kúszási mechanizmus mellett történt.
(a)
(b) 5. ábra A miszfit diszlokáció hálózat vonalaira meroleges szekciók. (a) Hexagonális hálózat, (R=0.34). (b) Módosított háromszög hálózat, R=0.15 A felületnek egy fontos tulajdonságát vehetjük észre az 5/b. ábrán: Míg a jobb oldalon az (101) síkok igen jól illeszkednek, addig a bal oldalon egy üreges rész keletkezik a felületen. Ennek a következménye a 3/b ábrán megfigyelheto jelenség is, miszerint jól láthatóan két különbözo jellegu háromszög alakú terület figyelheto meg. A magyarázat abban a tényben rejlik, hogy a háromszög szerkezetu diszlokáció hálózatot alkotó diszlokációk burgers vektorának a felületre meroleges komponense éppen az (111) síkok közötti távolságnak felel meg. Így amikor a diszlokációk kialakulnak, a felületen egy lépcso jelenik meg a diszlokációk vonala mentén. Az 5/a. ábrán látható hexagonális diszlokáció szerkezetnél nem figyelhetjük meg e lépcso vagy üresedés kialakulását. Ez az oka annak, hogy különbözo kötéserosségek mellett különbözo a diszlokáció szerkezeteket kapjuk, ugyanis az üresedés kialakulása által okozott energiatöbblet no a kötéserosség növekedésével. Így, ha az nagy, energetikailag kedvezobb egy hosszabb burgers vektorú díszlokációkból álló szerkezet kialakítása az üresedés létrejötte nélkül. Alacsonyabb kötéserosség mellett a lépcso kialakítása kedvezobb lehet, mint a hosszabb burgers vektorú diszlokációk megvalósulása. Komputer szimulációnkban atomi transzport nem jöhet létre. A valódi anyagban, ahol a diffúzió szerepet játszik, az esetlegesen kialakuló üregek azonnal feltöltodhetnek, ezáltal csökkentve a trianguláris hálózat energiáját. Hogy ezt a feltevést ellenorizzük, a modellkalkulációban kialakult üregeket, a háromfogású szimmetriát megorizve, feltöltöttük nióbium atomokkal, és a modellszámításokat így is elvégeztük. Az így kapott rendszerek kötéserossége nott (energiájuk csökkent). A különbözo számú atommal feltöltött rendszerek energiája azonban egymáshoz képest nagyon hasonló, azt sugallva, hogy a kialakuló atomi szerkezet nem feltétlenül teljesen meghatározott. Például a háromszögenként 98 illetve 143 atommal feltöltött rendszerek nagyon hasonló képet mutatnak.
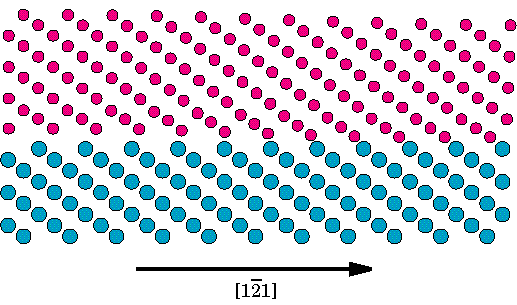
6. ábra A felülethez közeli Nb rétegekben a relaxáció során fellépett deformácio. R=0.15, A relaxáció során a felületen kialakult üresedéseket periodusoként 98 atommal töltöttük ki. A kialakuló diszlokáció háló háromszögszerkezetu, 1/2{111} típusú éldiszlokációkból áll. A 98 atommal feltöltött rendszer felülethez közeli Nióbium síkjainak elmozdulásterét mutatja a 6. ábra, R=0.15 mellett. Tökéletesen látszik, hogy a diszlokáció szerkezet trianguláris, háromszöges elrendezodést mutat, az 1. ábrának megfelelo burgers vektorokkal. Az elmozdulástér a 143 atommal feltöltött rendszer esetében is teljesen hasonló. A diszlokációk magjában az atomi elrendezodés azonban különbözik, ezt mutatja a 7/a. és 7/b. ábra, az atomi pozíciókat 5/b ábrával megegyezo módon ábrázolva. A 98 atommal feltöltött rendszer esetében a diszlokáció a felülethez van rögzülve, ellenben a 143 atommal feltöltött rendszerben a diszlokáció egyes szakaszokon egy (111) síknyival eltávolodik a határfelülettol (egy ilyen szakaszt mutat a 7/b. ábra).
(a)
7. ábra A miszfit diszlokáció hálózat vonalaira meroleges metszetek, R=0.15. (a) Az üresedéseket 98 atommal betöltve. (b) Az üresedéseket 143 atommal betöltve. Ahogy ez leolvasható, ebben az esetben a diszlokáció egyes szakaszain a felülettol egy réteggel eltávolodik. Mivel jelenlegi tanulmányunknak a fo célja a felületi kötéserosségnek és a felület atomi szerkezetének összekapcsolása, több különbözo R érték mellett végeztünk számolásokat az üregek feltöltésével. R<0.24 mellett a diszlokációk a felülethez kötve maradtak, noha néhol egy-egy rétegnyire eltávolodtak. Ezeknek a díszlokációknak a magja mind a 7/a. ábrának megfelelo, azzal, hogy növekvo R érték mellett az (101) síkok mind jobban és jobban meggörbülnek. Nagyobb R értékek mellett a diszlokációk az <121> típusú csúszósíkjuk mentén glide mechanizmussal a felülettol jelentosebb mértékben eltávolodnak. Ez látható a 8. ábrán, R=0.35 mellett. Az [1,-1,1] diszlokáció három (111) rétegnyire található a felülettol, magja szétterül az (121) csúszósíkja mentén. Az R érték növekedésével a diszlokáció további távolodása nem figyelheto meg. Ebben a távolságban a diszlokáció magja nagyon hasonló a bulk nióbiumban ugyanennek az éldiszlokációnak a magjához[41].
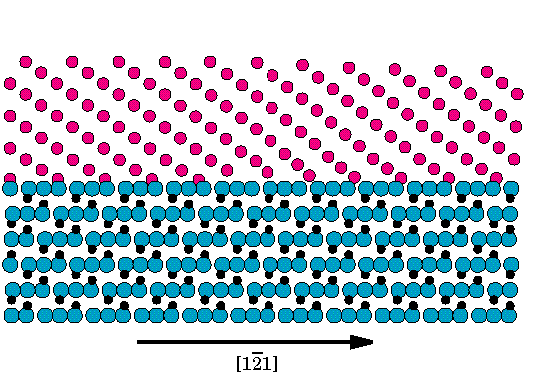
8. ábra. A miszfit diszlokáció hálózat vonalaira meroleges metszetek, R=0.35. A diszlokáció szinte teljes vonalában felülettol mintegy három rétegnyire helyezkedik el. HREM képszimulációk Az elektronmikroszkópos felvételek számítógépes eloállításához nem a modellezett szubsztrát szerkezetet használtuk, hanem a valódi, ideális, relaxálatlan zafírszerkezetet, a [41]-es referenciának megfeleloen. Ab initio számolások [31,32] alapján a zafír termináló rétegének egy oxigénsíkot választottunk. A zafír és a nióbium blokknak az egymáshoz képesti elhelyezkedését a korábban említett, a koherens részeken megfigyelheto speciális geometriai kapcsolat teljesítésének megfeleloen határoztuk meg. A képszimulációnak egy jellemzo kiinduló konfigurációját mutatja R=0.24 mellett a 9. ábra.
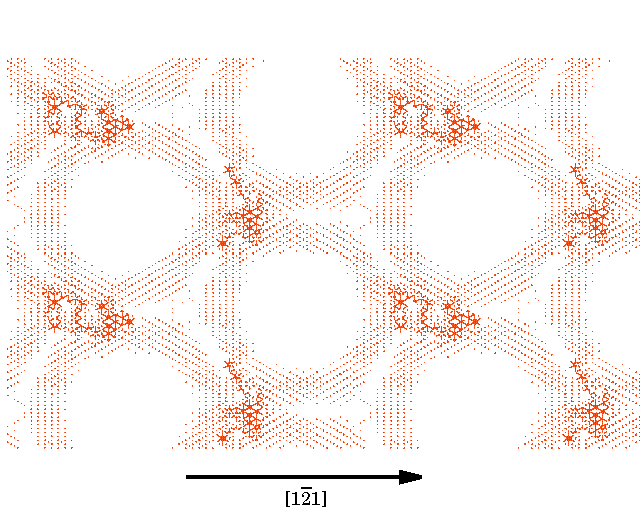
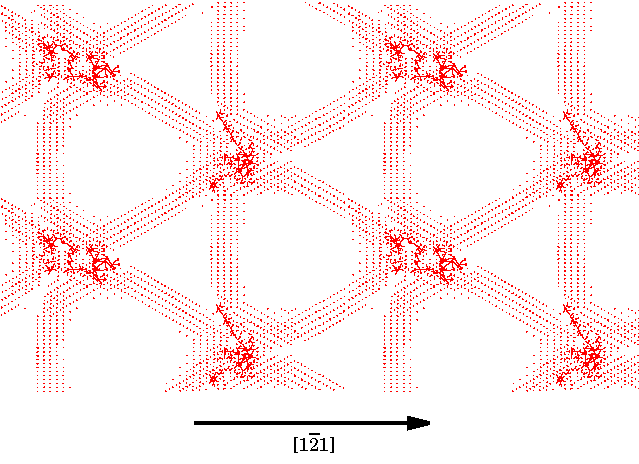
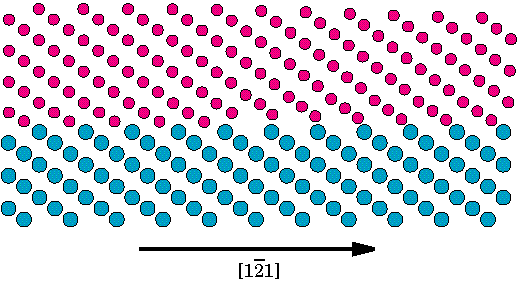
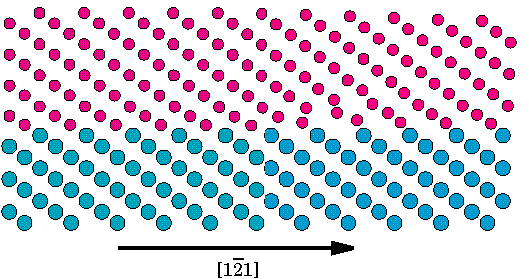
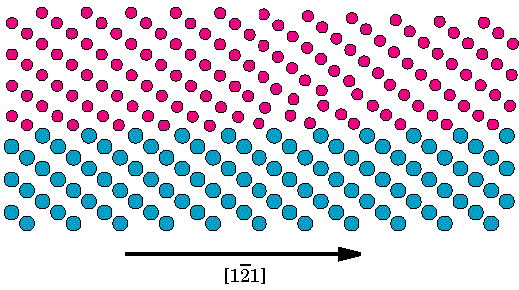
9. ábra A HREM képek szimulációjához használt blokk bemutatása. A felso, Nióbium rész az R=0.24 –hez tartozó számolás eredménye, míg az alsó rész a modell szubsztrát helyére helyettesített ideális zafír struktúra. Itt kis, sötét karikák az aluminum atomok, míg a nagyobbak, kékek az oxigén atomok. Az elektronmikroszkópos képeket az Electron Simulation Software (EMS) [48] programcsomagnak a “multislice” algoritmusának használatával állítottuk elo. Mintavastagságnak 6nm-t, defocus értéknek 40 nm-t használtunk, az elvégzett kisérleteknek megfeleloen[16,25,27,41], melyeket az NCEM Berkeley JEOL ARM 800 kV-os mikroszkópján végeztek el. Ezeket az értékeket a felülettol távoli anyagrészeknek valódi és szimulált felvételek hasonlósági elemzése alapján ellenoriztük. Elektormikroszkópos kísérletekkel a diszlokáció hálózatoknak csupán az elektronsugarakkal párhuzamosan eso díszlokációit lehet megfigyelni. Az atomi számolások eredményének képszimulációs felhasználásának így a céljai: (i) a hálózatoknak a képeken meglátszódó hatásának megfigyelése; (ii) a diszlokáció magszerkezetének illetve a felülettol való távolságának a kísérleti felvételek alapján történo megfigyelhetoségének vizsgálata; (iii) kísérleti és számolt képeknek az összehasonlítása. E cél érdekében a trianguláris hálózatnak három különbözo területérol készítettünk szimulált felvételeket, melyeket az 1. ábra árnyékolt részei mutatnak. Mindhárom típusú szimulációban az alkalmazott elektron nyaláb párhuzamos volt a diszlokáció egyenesével Az ’A’ terület jelentos részt tartalmaz a diszlokációk keresztezodési pontjából. A ’B’ terület tartalmaz tiszta diszlokáció szakaszt illetve egy részt a keresztezodésbol. Az ’A’ és ’B’ területeknél a multislice eljárást úgy alkalmaztuk, hogy az egyes szeletekben más és más struktúrát használtunk pontosan az atomi számolások eredményeinek megfeleloen. Ahogy ez késobb látható, ez a kontraszt gyengüléséhez vezet a képen amiatt, hogy a leképezésben sorra megjelennek a különbözo módon elforgatott illetve deformált nióbium rétegek. A ’C’ területnek a [1,0,-1] irányból pontosan egy periódusnyit választottunk. A multislice módszer segítségével ennek ismétlésével építettük fel a szükséges mintavastagságot. Ez megfelel annak, mintha egy tökéletes, egyenes, ?[1,-1,1] Burgers vektorú díszlokációról készítetünk volna felvételt, és megegyezik a multislice eljárás hagyományos alkalmazásával. Míg általában ez a módszer hozza létre a legnagyobb kontrasztot, kísérleti megvalósítása az erosen idealizált feltételek miatt szinte lehetetlen. A 10. Ábra a három módszer szerint számolt szimulált képeket ábrázolja R=0.24 értéknél és 98 atommal történt feltöltés mellett, amikor is a diszlokáció teljes hosszában (kivétel természetesen a diszlokáció keresztezodéseknél) a felületen helyezkedik el. Az ’A’ kép estében jelentos elkenodés figyelheto meg jó néhány (111) réteg távolságban a felülettol. Ennek oka nyilvánvalóan a diszlokációk keresztezodésének környékén meglévo nagy deformáció. A 9 és 7/a. ábrákkal való összevetésbol látható, hogy egy ehhez hasonló felvétel alapján nem lehetne egyértelmuen megkülönböztetni a két esetet. Ugyankkor a ’B’ és ’C’ esetben a szimulált kép és az atomi pozíciók között egyértelmu kapcsolat fedezheto fel. A ’B’ és ’C’ képek nagyon hasonlóak, ugyankkor a ’B’ esetben a leképzett mintában meglévo deformációk hatása kismértékben megváltoztatják a kontraszt elkenodését. Ez a tény azt mutatja, hogy a diszlokáció keresztezodéseknek csak akkor van jelentos hatásuk, ha a leképzett mintába közel teljes mértékben benne vannak. Megjegyzendo, hogy 143 atommal feltöltött modellszámítások alapján készített ’A’ és ’B’ típusú képek az itt bemutatotthoz nagyon hasonlóak, noha abban az esetben a diszlokáció egyes szakaszokon a felülettol kismértékben eltávolodik.
10. ábra Szimulált HREM képek az R=0.24 mellett talált háromszög elrendezésu miszfit diszlokáció hálózat ?[1,-1,1] díszlokációjáról. A felületi üresedést 98 atommal töltöttük fel. A három különbözo kép az 1. ábra A, B és C régiója alapján készült. A zónatengely [1,-1,0] a Nióbiumban, és [2,-1,1,0] a zafírban. Végezetül megállapíthatjuk, hogy az errol a diszlokáció hálózatról az irodalomban közölt felvétel[16,25,27,41] láthatóan jól egyezik a 10/B. illetve 10/C ábrán látható szimulált képekkel. Nem csak a díszlokációnak a felülethez rögzítettségében van hasonlóság, hanem a diszlokáció magjának környékén az (101) síkoknak a hajlása is megegyezik, amibol arra következtethetünk, hogy az atomi számolás a magszerkezet finomságait is helyesen tárta fel. Diszkusszió A (0001)||(111) zafír/nióbium határfelületének atomi modellezése alapján arra következtethetünk, hogy a felületen kialakuló diszlokáció hálózat háromszög-szerkezetu, a korábbi elektronmikroszkópos vizsgálatok eredményeinek megfeleloen[28]. Ugyanakkor a számolások azt mutatják, hogy az egyensúlyi diszlokáció hálózat kialakulásában a diffúziós folyamatok fontos szerepet játszanak. Ha diffúzió nem valósulhatna meg, akkor a háromszögszerkezetet csak nagyon gyenge adhézió mellet kaphatnánk. Az ?<111> típusú miszfit diszlokáció magszerkezete eros függést mutat a felületi adhéziótól. Gyenge adhézió esetén e diszlokációk magja (7/a. és 9. ábra) a felület irányában terjed ki, teljesen más képet mutatva mint a megegyezo bulk diszlokáció. Ilyenkor jellemzo, hogy az (101) síkok R-rel növekvo mértékben meghajlanak. Amikor a kötéserosség átlép egy kritikus értéket(R=0.25), a miszfit diszlokációk eltávolodnak a felülettol, de nem messzebbre mint három (111) síknyi távolság. Ezek az eredmények egyezésben vannak a korábbi, izolált miszfit díszlokációkra vonatkozó, hasonló számolásokkal. A HREM képszimulációk megmutatták, hogy amennyiben a miszfit diszlokációk keresztezodési pontja a HREM leképezésbe belekerül, jelentosen befolyásolja a kialakuló felvételt. Amikor a keresztezodés nem kerül bele a leképezésbe, a diszlokáció magszerkezete elég pontosan meghatározható ahhoz, hogy, a HREM felvételeknek az elméleti számolásokkal való összevetése alapján, hasonló esetekben következtetni lehessen a felületi kötéserosségre, energiaviszonyokra. Irodalom
Copyright © 2000 |
 (a).
(a).