Gouy, Debye–Hückel és Fick. Hogyan értsünk meg differenciálegyenleteket anélkül, hogy megoldanánk õket?

Amikor a töltött részecskék, például az ionok vagy a kolloid részecskék viselkedését próbáljuk megmagyarázni, elõjönnek a Coulomb-kölcsönhatások és végül a Poisson–Boltzmann-differenciálegyenletnél kötünk ki. Az egyenlet megoldása – bár a matematikával felvértezett hallgatókat nem hozza zavarba – igen hosszadalmas, és a matematikai mûveletek részletezése elvonhatja a figyelmet arról, amirõl az egyenlet szól. Ebben a rövid írásban egyszerû, intuitív módszert mutatunk be, amely azt illusztrálja, hogy a differenciálegyenleteket néha anélkül is értelmezhetjük, hogy megoldanánk õket.

Amikor a körülöttünk levõ fizikai világot kvantitatív, ellenõrizhetõ eszközökkel igyekszünk megérteni, rendszerint több fázison haladunk át. Elõször a problémát – fogalmilag – a leglényegesebb elemeire csupaszítjuk le, azután formába öntjük, majd megoldjuk. A fogalmi és a matematikai megfogalmazásnál általában leegyszerûsítjük a problémát (töröljük a kevésbé fontos részleteket), hogy a leglényegesebb részeket valamilyen szimbolikus rendszer – most például a matematika, pontosabban egy differenciálegyenlet – segítségével fejezhessük ki. A megoldás az egyenletek kezelése annak érdekében, hogy a paraméterekre explicit kifejezéseket kapjunk. Amikor kvantitatíve igazolható eredményekre törekszünk, nem hagyhatjuk ki a formulák megfogalmazásának fázisait. Ez az írás csak a megoldás fázisát tárgyalja, s elkerüli az explicit matematikai megoldások keresésével járó hosszadalmas munkát.

Elõször az elektromos kettõsréteg problémáját írjuk le, majd levezetjük a megfelelõ matematikai összefüggést. A problémát leíró differenciálegyenletet azonban nem oldjuk meg, hanem néhány dimenziómentes mennyiségbõl következtetünk az egyenletben rejlõ legfontosabb információkra. Ezután a Debye–Hückel-egyenletet vizsgáljuk meg, és megmutatjuk, hogy igen hasonló módon kezelhetõ, mert matematikailag lényegében az elõzõvel azonos probléma. A módszert a Fick-egyenletre is alkalmazzuk.
 

Az elektromos kettõsréteg

A századforduló táján Georges Gouy, a kor egyik nagy, de többé-kevésbé elfeledett tudósa, az elektrokémikusok gyakori foglalatosságát ûzve a molekulák és az ionok adszorpcióját vizsgálta a higanylektród és a vizes oldat közötti határfelületen. Molekulák esetében a probléma viszonylag egyszerû, mert a molekulák a higanyelektróddal mindig rövid távú kölcsönhatásokba bocsátkoznak (például a kovalens vagy hidrofób kölcsönhatások esetén), vagy legfeljebb a molekulák dipólus momentumainak és polarizálhatóságainak függvényei. A dipól kölcsönhatások erõssége meredeken csökken a távolság függvényében, amint a távolság naggyá válik a dipólus töltésszétválásához képest. A polarizálhatóság hatása még lokálisabb. A fém–oldat határfelületen lejátszódó molekuláris adszorpció ezért az adszorbátum és a fém közötti közvetlen érintkezés feltevésével írható le. Ez az elképzelés megfelelt az akkoriban elfogadott, Helmholtz-féle higany–víz határfelület modellnek, amely szerint a határfelületen egyetlen réteg adszorbeált molekula vagy ion van.

Az ionok azonban hosszú távú Coulomb-kölcsönhatásokat hoznak létre az elektromos határfelülettel, s emiatt nincs szükség érintkezésre. Ezért az ionok az elektrosztatikus vonzásra és taszításra már akkor is reagálhatnak, ha az elektród szomszédságában vannak, s ebben az esetben mind az elektrosztatikus vonzásnak vagy taszításnak, mind a hõmozgásnak ki vannak téve. A feladat tehát az elektrosztatikus kölcsönhatás és a hõmozgás közös hatásának leírása. Ezt oldotta meg Gouy. A fémen levõ elektromos töltést és a szomszédos oldatban levõ ionos töltést elektromos kettõsrétegnek nevezik. Ebben a tartományban nincs lokális elektroneutralitás, ezért tértöltési rétegként is említik.

Az alábbiakban Gouy módszerét fogjuk követni számos egyszerû esetben; elõször egyetlen z,z-elektrolitot tekintünk – ilyen például a NaCl vagy a MgSO₄ – és síkelektródot vizsgálunk, tehát csak egyetlen térbeli paramétert, a fém–oldat határfelülettõl mért x távolságot kell figyelembe vennünk.
 

A Poisson–Boltzmann-differenciálegyenlet

Az elektrosztatika és a hõmozgás együttes hatását leíró elsõdleges összefüggés a Boltzmann-egyenlet. Ezzel a formulával adjuk meg a kationok és az anionok lokális koncentrációját a lokális y potenciál függvényében:
 

	(1)
	(2)

ahol c₊ és c_– a lokális kation- és anionkoncentráció a távolság függvényében, és c* a só oldatbeli koncentrációja a határfelülettõl elegendõen nagy távolságban, ahol a határfelület hatása már nem érzékelhetõ, tehát y =0. Az F, R és T paraméter a szokásos Faraday-állandó, gázállandó és abszolút hõmérséklet. Az exponenciálisokban az elõjelek arra utalnak, hogy a pozitív y  potenciál a kationokat taszítja, az anionokat vonzza, míg a negatív potenciál ellentétes hatású. NaCl esetében |z|=1, mert mind a Na⁺, mind a Cl^–  egy vegyértékû ion;  MgSO₄ esetében |z|=2.

A másik szükséges összefüggés, a Poisson-egyenlet, a potenciál és a lokális töltéssûrûség kapcsolatát írja le. Síkbeli geometriánk esetében:
 

(3)

ahol r a lokális töltéssûrûség (egységnyi térfogatra számítva), és e az oldat dielektromos permittivitása (vagy dielektromos "állandója"). A határfelülettõl távol mind y , mind r zérus, de az elektród közelében kation- vagy aniontöbblet alakulhat ki. Egyetlen z,z-elektrolit esetében a lokális töltéssûrûség:
 

(4)

ahol a (coulomb/mól-ban kifejezett) Faraday-állandó a kémiai számsûrûséget (vagyis a mól/térfogatban kifejezett koncentrációt) elektromos töltéssûrûséggé alakítja át (az utóbbi dimenziója coulomb/térfogat).

Ez a négy összefüggés adja együtt a Poisson–Boltzmann-egyenletet:
 

(5)

Az eredmény igen bonyolultnak tûnik, de jelentõsen egyszerûsíthetõ a dimenziómentes y=|z|Fy /RT paraméter bevezetésével, ami az (5) egyenletet a következõ alakra hozza:
 

(6)

Információszerzés az egyenlet megoldása nélkül

Ahelyett, hogy megoldanánk, nézzük meg alaposan az egyenletet! Mivel y dimenziómentes, a (6) egyenlet bal oldalának 1/x² a dimenziója, ahol x távolság. A (6) egyenlet jobb oldalának zárójeles kifejezése dimenziómentes, ezért z²F²c*/eRT-nek is 1/x² a dimenziója (vagyis reciprok távolságnégyzet). Továbbá a z²F²c*/eRT az egyetlen olyan változó a (6) egyenletben, amely függ a kísérleti körülményektõl. Ezért eRT/z²F²c* négyzetgyökének a probléma karakterisztikus távolságának kell lennie. Ezt a távolságparamétert, amely az elektród melletti tértöltési réteg karakterisztikus távolságát reprezentája, Gouy [1,2] a-val vagy a-val jelölte. Ma általában a reciprokát (k=1/a) használják, amelyet Debye és Hückel vezetett be [3].

Bevezethetünk azonban egy másik dimenziómentes paramétert is: x=x/x_kar=xÖ(eRT/z²F²c*), s így a (6) egyenlet a következõ alakot ölti: d²y/dx²=e^–y–e^+y. Nyilvánvaló, hogy a dimenziómentes y potenciál viselkedését teljesen  meg kell határoznia a x=x/x_kar értéknek, tehát a karakterisztikus távolság, x_kar szerint szerint skálázott x értéknek.

Érdemes most visszatekinteni a fenti levezetésre, hogy észrevegyük: a felhasznált egyenletek érzéketlenek a sók kémiai jellegére, és csak az ionok vegyértékeit tartalmazzák. Ezért a meggondolás könnyen kiterjeszthetõ a z,z-elektrolitok keverékeire – ilyen például a KCl+NaClO₄+LiH₂PO₄ vagy a MgSO₄+BeSO₄–, ha a (4) egyenletet a
 

(4')

kifejezéssel helyettesítjük. Ekkor az (5) és (6) egyenlet a következõképpen alakul:
 
 

	(5')
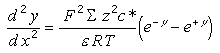	(6')

A tértöltési réteg a karakterisztikus vastagsága:
 

(7)

reciproka:
 

(8)

Figyeljük meg, hogy a c* sókoncentráció ezekben a kifejezésekben a Sz²c* kifejezés négyzetgyökében jelenik meg. Gouy [2] a leggyakoribb aszimmetrikus sók, például a Li₂SO₄, a CaCl₂, a Na₃PO₄ és az Al(NO₃)₃ esetében is elemezte a megfelelõ eredményeket, Levine és Jones [4] pedig egy és két vegyértékû ionok tetszõleges keverékeire is kiterjesztette a számítást. A meghatározó tulajdonság minden esetben Sz_i²c_i*, ahol az összegzés az összes i ionra kiterjed. Egyetlen 1,1-elektrolit esetében ez az összeg a sókoncentráció kétszerese, ezért célszerûbb a felét, 1/2Sz_i²c_i*-t  tekinteni; ezt a paraméterkombinációt Lewis és Randall [5] ionerõsségnek nevezte el. A tértöltési réteg a=1/k karakterisztikus vastagsága vizes oldatban, szobahõmérsékleten 10, 3, 1 és 0,3 nm, ha az ionerõsség rendre 0,001, 0,01, 0,1 és 1 M.

A tértöltési réteg teljes leírásához természetesen meg kell oldani a fenti egyenleteket. Most csak annyit jegyzünk meg, hogy gyakran kapunk jó közelítést, ha feltesszük, hogy a határfelülettõl távolodva a potenciál exponenciálisan csökken, tehát
 

(9)

ahol y_o a-tól (vagy k-tól) és a fémen kialakuló felületi töltéssûrûségtõl függ [6]. A jelenlegi tárgyalás szempontjából igen fontos, hogy mind y_o, mind a=1/k az ionerõsség növekedésével csökken. A Gouy-modell érvényességét a legközvetlenebb módon Israelachvili és Adams elegáns kísérletei [7] igazolták.
 

Alkalmazások
Kolloid szuszpenziók stabilitása

Nemcsak fémek, hanem kolloidok, például AgCl-részecskék körül is kialakulnak elektromos kettõsrétegek. Ekkor a felületi töltéssûrûséget a többletionok (akár Ag⁺-, akár Cl^–-ionok) hozzák létre a fémek elektronjai helyett, de minden más ugyanúgy érvényes, mint az elõbb. Tegyük fel, hogy az ezüst-nitrát oldatba adagolt nátrium-klorid oldattal ezüst-klorid csapadékot hozunk létre. Kezdetben az oldat olyan többlet ezüstionokat tartalmaz, amelyek még nem csapódtak ki. A többlet ezüstionok némelyike a megfelelõ rácshelyekre épülhet be az ezüst-klorid részecskéken. Ezek az ezüst-klorid részecskék pozitív töltésre, s így pozitív y_o-ra tesznek szert, ezért olyan anionokkal, ebben az esetben nitrátionokkal veszik magukat körül, amelyek nem épülnek be a kristályba. Az összes AgCl-részecske körül tértöltési réteg alakul ki. Mivel ezek a rétegek taszítják egymást, a részecskék nem közelíthetik meg tetszõlgesen egymást, tehát nem állhatnak össze nagyobb képzõdményekké. Olyan kicsik maradnak, hogy sokszor a szûrõn is átszaladnak. A kölcsönösen taszító elektromos kettõsréteggel körülvett, kis, töltött részecskék szuszpenziója kolloid szuszpenziót képez. Többlet NaCl hatására a tértöltési rétegek ellentétes töltésûvé válhatnak: többlet Cl^– lesz a felszínükön, és azok a kationok hozzák létre a tértöltési rétegek, amelyek nem épülnek be a kristályrácsba (ezúttal a nátriumionok).

A szuszpenziót úgy vihetjük oldatba, ha egy másik, csapadékot nem képezõ elektrolit adagolásával csökkentjük a y_o potenciált és az a=1/k rétegvastagságot. Ez az eljárás nem intuitív eredmény, hanem az elméletbõl következik, és kísérletekkel is alaposan igazolták. A töltött kolloid szuszpenziók stabilitására vonatkozó Gyerjagin–Landau–Verwey–Overbeek-modell [8,9] valójában a Gouy-elméleten alapszik.
 

Ionos kölcsönhatások

Az ionkristályokban, például a szilárd nátrium-kloridban, azonos számú kation és anion van, mégis mindegyiket elsõsorban a másik fajtához tartozó ionok veszik körül, ezért elektrosztatikus vonzás hat rájuk. A szilárd nátrium-kloridban például a Na⁺- és a Cl^–-ionok körülbelül 1,75-ször nagyobb elektrosztatikus vonzást érzékelnek, mint egyetlen ellenion jelenlétében észlelnének, ha ez az ion a lehetõ legjobban megközelítené õket [10].

Az elektrolitoldatban az ionok között természetesen vízmolekulák is vannak, és az ionok nem szabályos rácshelyeken ülnek, hanem hõmozgást végeznek. A vonzó ionos kölcsönhatás azonban megmarad: a kationok az anionok közelében fordulnak elõ a legnagyobb valószínûséggel (és fordítva). Debye és Hückel [3] ennek a problémának a leírását matematikailag kezelhetõ problémára egyszerûsítette: az izolált iont olyan hipotetikus, egyenletesen szétkent töltéstengerbe, ionfelhõbe helyezte, amelynek teljes töltése éppen ellentétes a kiválasztott ionéval. Az eredményül kapott Poisson–Boltzmann-egyenlet nagyon hasonlít Gouy egyenletéhez azzal a kivétellel, hogy a központi ion körül gömbi geometriával számol. A levezetés ugyanaz, mint az (1)–(6) egyenletek esetében, de a Poisson-egyenletet most gömbi koordinátákban írjuk fel:
 

(10)

Egyetlen z,z-elektrolitra a következõ eredmény adódik:
 

(11)

ahol r a központi iontól mért radiális távolság; a dimenziómentes y paraméter definíciója ugyanaz, mint az elõbb, vagyis y=|z|Fy /RT. Figyeljük meg, hogy az (11) egyenlet jobb oldala hasonlít a (6) egyenletéhez, és bal oldalának dimenziója ismét reciprok távolságnégyzet, 1/r². Tehát most is az elõbbi gondolatmenetet alkalmazhatjuk: a (7) és (8) egyenlettel kifejezett a=1/k távolság az egyes ionok körüli tértöltési réteg sugarát határozza meg, és az 1/2Sz_i²c_i* ionerõsség ismét a koncentráció hatását méri. Ez az oka annak, hogy a Debye–Hückel-elméletbõl következõ aktivitási koefficienseket az ionerõsség négyzetgyökének függvényében ábrázolják, és a y potenciált közelítõleg a y_oexp[–r/a]=y_oexp[–kr] kifejezés adja meg.
 

További eredmények, következmények

A fenti eljárás segítségével – pusztán a dimenziókat vizsgálva – a Poisson–Boltzmann-differenciálegyenletbõl megkaphatjuk a karakterisztikus a vagy k paramétert, amely leírja a töltött elektród, a töltött mikroszkopikus részecske, például kolloid vagy ion körüli tértöltési réteg kiterjedését. A kolloid részecskék akkorák, hogy (átlagos) görbületi sugaruk rendszerint sokkal nagyobb, mint a=1/k; ebben az esetben a görbület elhanyagolható, és a Poisson-egyenlet síkgeometriára vonatkozó alakja használható. Ionok esetében ez a közelítés nyilvánvalóan nem használható; a Poisson-egyenlet gömbi alakját kell alkalmazni. Az a=1/k mennyiség azonban mindkét esetben megadja a tértöltési réteg karakterisztikus vastagságát, vagyis annak a távolságnak a nagyságrendjét, amelyen az elektroneutralitás nem áll fenn.

Általában a kolloidok kicsapódásának és az elektrolitoldatok aktivitásának példáján vezetik be a hallgatóknak a tértöltési réteg fogalmát: a két rokon problémában ugyanaz az egyenlet és ugyanaz a dimenziómentes paraméter játszik hasonló szerepet. Ha például membránban oldódó ionok vagy ionhordozó komplexek vándorolnak lipid kettõsrétegen, a Poisson–Boltzmann-egyenlet mellett a Nernst–Planck-egyenletet is figyelembe kell venni a diffúzió és a vándorlás leírására, s nemcsak a membránok szomszédságában, hanem a belsejükben is kialakulhatnak tértöltési rétegek [11].

Amikor arra törekszünk, hogy a matematikai egyenletek megoldásait zárt alakban állítsuk elõ, az egyenletek tartalmára nem mindig jut kellõ figyelem. Sok vegyészhallgató nem elég jártas ezeknek az egyenleteknek megoldásában; de még ha gyakorlott is, a kémiának nem a matematikai megoldás részleteire, hanem az egyenletek fizikai és kémiai következményeire kell figyelnie. Kedvezõ esetben, mint a mostani példában, a legfontosabb információkat az egyenletek megoldása nélkül is megszerezhetjük az egyenletekbõl. Az explicit megoldások gyakran igen bonyolultak, ezért nehezen szemléltethetõk; az itt bemutatott módszerrel ez a nehézség is elkerülhetõ. A karakterisztikus paraméterkombinációra koncentrálva azonnal a probléma lényegét ragadjuk meg.

Furcsa módon a legújabb eszközök, például a szimbolikus megoldásokat szolgáltató Maple vagy Mathematica programok általában nem sokat segítenek. Még ha megtalálják is a megoldást (ami a Gouy-modell esetében sikerül, a Debye–Hückel-egyenletnél már nem), az eredmény olyan bonyolult, hogy alig értelmezhetõ.

Az itt bemutatott gondolatmenet természetesen nemcsak a Poisson–Boltzmann-egyenletre korlátozódik. Például a diffúziós tömegtranszportot leíró Fick-törvény legegyszerûbb, egydimenziós alakja

1. Gouy, G. C. R. Acad. Sci. 1909, 149, 654.
2. Gouy, G. J. Phys. (Series 4) 1910, 9, 457.
3. Debye, P.; Hückel, E. Phys Z. 1923, 24, 185.
4. Levine, S.; Jones, J. E. Kolloid Z. 1969, 230, 306.
5. Lewis, G. N.; Randall, M. J. Am. Chem. Soc. 1921, 43, 1112.
6. de Levie, R. J. Electroanal. Chem. 1990, 278, 17.
7. Israelachvili, J. N.; Adams, G. E. J. Chem. Soc. Faraday Trans. 1, 1978, 74, 975.
8. Gyerjagin, B.; Landau, L. Acta Physicochim. URSS  1941, 14, 633.
9. Verwey, J. W.; Overbeek, J. T. G.: Theory of the Stability of Lyophobic Colloids, Elsevier: Amsterdam, 1948.
10. Madelung, E. Z. Phys. 1918, 19, 524.
11. de Levie, R.; Moreira, H. J. Membrane Biol. 1972, 9, 241.
12. Fick, A. Ann. Phys. 1855, 170, 59.