Fourier elmélete a hôvezetésrôl

A hôszubsztancia elmélet egyik legnagyobb sikere FOURIER nevéhez fûzôdik, aki kidolgozta a hôvezetés matematikai elméletét.

Fourier problémája: a t = 0 idô- pillanatban a testben valamilyen hômérséklet-elosztást valósítunk meg. Kérdés, hogyan változik a  hômérséklet a test különbözô pontjaiban az idô függvényében

JEAN BAPTISTE JOSEPH FOURIER szegény sorsú családból származott. Tehetségének kibontakozását a forradalom, majd NAPÓLEON biztosította. Már 1807-ben elkezdte hôvezetéssel kapcsolatos vizsgálatait, de cikkét szigorú bírálói – LAGRANGE, LAPLACE és LEGENDRE – közlésre nem javasolták. Idevágó eredményeit 1822-ben megjelent Théorie analitique de la chaleur címû könyve foglalja össze. Ebben nagyon világos fizikai elképzelésbôl indul ki, és a matematikai problémát igyekszik szemléletessé tenni. Képzeljünk el egy testet valamilyen kezdeti hômérséklet-eloszlással. Ezt úgy szemléltethetjük, hogy a test különbözô pontjaiba kis hômérôket képzelünk, amelyek mindegyike kiinduláskor valamilyen meghatározott, esetleg azonos értéket mutat. A test felületén keresztül a hôt átadja környezetének, a belsejébôl pedig a hô a felületek felé áramlik. Így természetesen a hômérôk, a test különbözõ helyein egy adott idôpillanatban, más-más értéket fognak mutatni (bal oldali ábra). A matematikai vizsgálat célja az, hogy ezen hômérôk által mutatott értéket határozzuk meg mint a hely és az idô függvényét.

Mind a matematika, mind a fizika történetében FOURIER vizsgálatai alapvetô jelentôségûek: FOURIER ugyanis azt találta, hogy a matematikailag megfogalmazott probléma megoldását, legalábbis ami a legegyszerûbb esetben a térbeli változást illeti, különbözõ argumentumú sinusfüggvények, illetôleg ezek kombinációi adják. Minthogy a kiinduló helyzet, vagyis a hômérséklet-eloszlás a vizsgálat kezdetekor, kizárólag tôlünk függ, felmerül az a kérdés, hogyan lehetséges egy tetszés szerinti függvény összerakása tiszta sinusfüggvények segítségével. Matematikai nyelven szólva: hogyan fejthetô egy tetszés szerinti függvény Fourier-sorba. A FOURIER által adott megoldásból így a matematikának egy külön ága, a Fourier-sorok elmélete fejlôdött ki, a fizika pedig problémái megoldásához a Fourier-sorokban egy igen hatékony módszert talált.
 

Caloricum és állapotegyenlet

A caloricumelmélet azonban nemcsak a hôáramlással kapcsolatban tudott érdemlegeset mondani. LAPLACE megkísérelte, hogy a gázok állapotegyenleteit is levezesse ezen elmélet alapján. Mai szemmel olvasva levezetését, elismeréssel kell adózni egy matematikai zseni hipotézis- és képletzsonglôri ügyességének. Kiindul abból az alapfeltevésbôl, hogy az egyes anyagrészek között az anyagrészeket felhôként körülvevô hôszubsztancia következtében taszítóerô lép fel, amelyet az alábbi képlet fejez ki:

Ebben a formulában H egy állandót jelent, c a caloricum sûrûsége, j(r) pedig egy, a távolsággal igen gyorsan csökkenô függvényt jelent. Itt lépnek fel elôször a rövid hatótávolságú erôk. LAPLACE ezen erôk összességével eljut a gáznyomás alábbi formulájához:

Ebben a formulában K az egy anyagrészre ható erôk eredôjét jelenti. Ez még végtelen sok részecske esetén is véges értékû, minthogy az erôk, mint említettük, rövid hatótávolságúak. Ez a formula szemmel láthatóan rossz, mert az anyag sûrûsége(r) a négyzeten szerepel a helyes elsô hatvány helyett. Erre a kérdésre azonban LAPLACE könnyedén meg tud felelni: az anyag sûrûsége és a caloricum sûrûsége nem független egymástól, hanem a sugárzási egyensúly következtében egy

alakú kapcsolat áll fenn közöttük, ahol a jobb oldal már kizárólag csak az u hômérséklettôl függ. Így azután LAPLACE megkapja a helyes

kapcsolatot. Ez az egyenlet teljesen azonos alakú a Gay-Lussac-törvénnyel, ha LAPLACE nyomán a kizárólag a hômérséklettôl függô P(u) mennyiséget azonosítjuk magával a hômérséklettel.

LAPLACE elméletének legnagyobb teljesítménye az volt, hogy ilyen alapon le tudta vezetni az adiabatikus állapotváltozás
állapotegyenletét is.
 

A Carnot-ciklus

A hôerôgépek hatásfokának növelésével kapcsolatban a gyakorlat és elmélet összekapcsolásának szükségességét különösen JAMES WATT hangsúlyozta. Ezen témakörbe illeszthetôk SADI CARNOT vizsgálatai. Ô még úgy képzelte el a hôerôgépek mûködését, mint ahogy a vízerôgépek mûködését: a magasabb szintrôl alacsonyabb szintre lezúduló vízmenynyiség szolgáltatja a mechanikai munkát, a hôerôgépeknél a magasabb szintet a magasabb hômérséklet jelenti, a lezúduló vízmennyiségnek pedig a hasonlóképpen átalakulást nem szenvedô hôszubsztancia felel meg. Ezen analógia tehát egy gôzgép hatásfokára az alábbi összefüggést adja:

A munka létrejötte egy vízerôgépben, egy  hôerôgépben és egy egyenáramú villamos  motorban. A hatásfokra ugyan helyes ered- ményt kapunk, de az analógia a hôerôgép esetén teljesen hamis: a hô – miközben a magasabb szintrôl alacsonyabb szintre áramlik – mennyiségében is megváltozik. Carnot ezzel még nem volt tisztában: Jogosan hasonlíthatjuk össze tehát a hô  mozgató erejét a víz esésével. A víz esé- sének mozgató ereje a magasságtól és a folyadék mennyiségétôl függ: a hô moz- gató ereje az alkalmazott caloricum meny- nyiségétôl, valamint – amit mi éppen az  esés magasságának is nevezhetnénk – azon hômérséklet különbségétôl, amely a hôt kicserélô testek között fennáll CARNOT: Reflexion sur la puissance...

Mindezek után az olvasó talán meglepetéssel veszi tudomásul, hogy a CARNOT által felírt hatásfokképlet hibátlan: ma is ezzel a formulával számolunk. Ennek igen egyszerû a magyarázata. Az elôbb mondottak értelmében ugyanis, ha Q₁ hômennyiséget táplálunk egy meghatározott idô alatt a hôerôgépbe T₁ hômérsékleten, és ugyanezen idô alatt Q₂ hômennyiséget viszünk el T₂ hômérsékleten, akkor mechanikai munkává – legalábbis ideális esetben – a Q₁–Q₂ különbség alakul át, így tehát a hatásfok:

Ma már tudjuk, hogy a CARNOT által vizsgált körfolyam, az úgynevezett Carnot-ciklus esetén fennáll a következô összefüggés:

vagy másképpen írva:

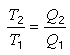
Ez tehát annyit jelent, hogy CARNOT eredetileg hibás elképzelése alapján levezetett formulája teljes egzaktsággal érvényes. CARNOT egyébként késôbbi éveiben – mint ahogy ez levezetéseibôl és feljegyzéseibôl kitûnik – tisztán kezdi látni a hô és a mechanikai munka egymásba alakíthatóságának kérdését. Korai halála azonban megakadályozta abban, hogy ezen a téren a döntô lépést megtegye. De hogy az energiamegmaradás tételéhez milyen közel jutott, az alábbi idézet is bizonyítja.

Valaki talán azt az ellenvetést tehetné, hogy bár a perpetuum mobile lehetetlensége pusztán mechanikai hatások esetére bizonyítva is van, esetleg nem így áll a dolog, ha a hô és a villamos hatásokat is felhasználjuk; de vajon elgondolható-e a villamos- és hôjelenségek számára valami más ok, mint a testek valamiféle mozgása és ezek nem lennének alávetve a mechanika törvényeinek? Egyébként pedig nem tudjuk-e a posteriori, hogy minden próbálkozás a perpetuum mobile megvalósítására – bármilyen módszerhez is folyamodtak – terméketlen maradt? Hogy soha senkinek sem sikerült egy valóságos perpetuum mobilét elôállítani, vagyis egy olyan mozgást, amely szakadatlanul, a felhasznált test legkisebb változása nélkül folytatódik.

Felmerült ugyan a gondolat, hogy az elektromos készülék (a Volta-oszlop) alkalmas arra, hogy egy perpetuum mobilét létrehozzon; ezt a gondolatot száraz oszlopok elôállításával próbálták megvalósítani, amely oszlopokat változatlannak tekintettek. De bárhogyan is igyekeztek, végül is a készülék mindig érezhetô elhasználódást mutatott, ha hatását bizonyos energiával meghatározott idôn keresztül kifejtette.

A perpetuum mobile általános és filozófiai fogalma nemcsak egy olyan mozgás képzetét tartalmazza, amely az elsô meglökés után végtelenségig folytatódik, hanem egy olyan berendezés vagy szerkezet képzetét is, amely alkalmas arra, hogy korlátlan mennyiségben mozgató erôt hozzon létre, amely tehát képes a természet összes anyagrészeit, ha azok nyugalomban vannak, egymás után mozgásba hozni és ezzel a tehetetlenség elvét hatástalanítani és végül képes arra, hogy önmagából merítsen erôt ahhoz, hogy végül is az egész világegyetemet mozgásba hozza, abban megtartsa és folytonosan gyorsítsa...

Ha ez ténylegesen lehetséges lenne, akkor teljesen fölösleges lenne, hogy a mozgató erôt a levegô és víz áramlásában, vagy az éghetô anyagokban keressük; a mozgató erô kimeríthetetlen forrásával rendelkeznénk, amelybôl tetszésünk szerint meríthetnénk.

Simonyi Károly: A fizika kultúrtörténete, 3., átdolgozott kiadás, Gondolat Kiadó, Budapest, 1986, 340., 342–344. o.