Molekuláris oldatkémia
A rácsmodellektõl a molekuladinamikai konfigurációkig
Pálinkás Gábor
a Magyar Tudományos Akadémia levelezõ
tagja
Elõadásom végéhez közeledve engedjék meg, hogy néhány példán keresztül illusztráljam azokat a lehetõségeket is, amelyeket az oldatok molekuladinamikai modellezése nyújt számunkra az oldatok dinamikájának vizsgálatához.
3. táblázat
| Egyedi öndiffúziós állandók LiI vizes oldatában (c = 2.2 mol·kg–1) |
Dw | DLi | DI | |
| |
Vízmolekulák öndiffúziós állandói |
Di | |
| MD | 2.48 | 0.7 | 1.40 | | | tömbfázis | 2.85 | |
| Kis. | 2.35 | 1.0 | 1.47 | | | kation hidrátszféra | 1.33 | |
| (105 cm2s–2) | | | anion hidrátszféra | 2.67 |
Említettem korábban, hogy a molekuladinamikai modellek elõállítják
az oldatok specieseinek, az oldószer molekuláknak és
ionoknak, sebesség autókorrelációs függvényeit.
A sebesség autókorrelációs függvényekbõl
számítható öndiffúziós állandók
összehasonlítása a kísérleti adatokkal
a modellek minõségének egyik próbája.
Egy ilyen összehasonlításra láthatunk példát
a 3. táblázatban, amely tömény LiI vizes oldat
specieseinek számított és nyomjelzéses kísérleti
technikával mért öndiffúziós állandóit
tünteti fel. Az ábrán szereplõ táblázatban
láthatunk példát olyan egyedi tulajdonságok
számítására is, amelyek kísérletileg
nem elérhetõk. Nevezetesen, mivel a modellben a részecskék
megkülönböztethetõk, külön számítható
mind a tömbfázisban, mind az ionok hidrátszférájában
elhelyezkedõ vízmolekulák öndiffúziós
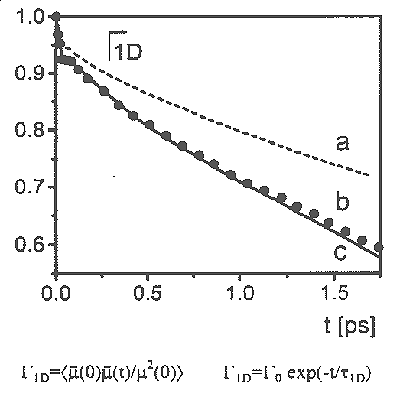
állandója. Hasonló példát mutat be a
26. ábra is, amely a tömbfázisú és hidratált
vízmolekulák dipólus autókorrelációs
függvényekbõl számítható átlagos
reorientációs idõit tünteti fel. Ezek az egyedi
részecske tulajdonságok fontos információt
hordoz-nak a különbözõ környezetû vízmolekulák
mozgásállapotáról.

| r1D (ps) | |
| a. Li+ hidrátszféra b. Cl– hidrátszféra c. tömbfázis |
6.8 4.6 4.4 |
26. ábra
Érdekes jelenséget figyelhetünk meg NaCl és MgCl2 sók metanolos oldatainak molekuladinamikai modelljeiben számított sebesség autokorrelációs függvényeken (27. ábra). A sebesség autokorrelációs függvények elsõ zérushelye azt az átlagos idõt jellemzi, amely alatt egy adott részecske visszalökõdés mentesen mozog. Ezt követõen a függvény elõjelet vált, a részecske mozgásának iránya megfordul. Összehasonlítva az ábrán az oldószer molekulák és az ionok visszalökõdéséhez szükséges karakterisztikus idõket megfigyelhetjük, a kationok – de különösen a kis ionsugarú Mg++ kation – rezgõmozgását a szolvatált oldószer molekulák üregében (cage).
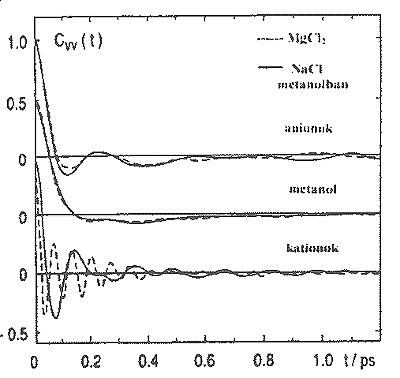
27. ábra
Összehasonlítva az ábrán az oldószer molekulák és az ionok visszalökõdéséhez szükséges karakterisztikus idõket megfigyelhetjük, a kationok – de különösen a kis ionsugarú Mg++ kation – rezgõmozgását a szolvatált oldószer molekulák üregében (cage).
Említésre érdemes az is, hogy a flexibilis molekulakulamodellel
dolgozó modell reprodukálja az oldószer molekulák
OH nyújtási rezgéseinek erõs vöröseltolódását
Mg++ kationok hatására (4. táblázat).
Az intenzív kation-oldószer kölcsönhatás
miatt fellépõ jelenséget infravörös mérések
igazolják.
4. táblázat
A metanol molekulák rezgési sávjainak eltolódása ionok szolvátburkában
| OH ny. | COH h. | CO ny. | |
| tömbfázis | 3344 | 1406 | 1045 |
| Cl– | 3368 | 1404 | 1045 |
| Na+ | 3291 | 1407 | 1043 |
| Mg++ (cm–1) |
3000 | 1440 | 1064 |
Az elõadásomban a rendelkezésemre álló
idõ alatt csupán a molekuladinamikai modellek néhány
alapvetõ oldatkémiai problémára adott válaszát
kísérelhettem meg ismertetni Önökkel. A számítógépes
lehetõségek rohamos bõvülése ma már
lehetõséget ad az ismertetett jelenségeknél
jóval bonyolultabb, összetettebb oldatkémiai jelenségeknek
modellezésére is. Számos eredmény született
biológiailag aktív molekulák hidratációs
jelenségeinek vizsgálatában, szelektív iontranszport
modellezésében membránokban vagy határfelületi
jelenségek értelmezésében. A lehetõségek
bõvülését jelzi kvantumszimulációk
megindulása is, amelyekben a klasszikus hipotézist elhagyva,
a sokrészecske rendszerek sûrûségmátrixainak
idõfüggését Monte Carlo módszerrel szimulálják.
Köszönetnyilvánítás
Elõadásom végére érve szeretnék köszönetet mondani mindazoknak, akik hozzájárultak ahhoz, hogy munkámat, elvégezhettem és a Kémiai Osztály abban a megtiszteltetéstetésben részesített, hogy tagjai közé választott.
Talán az elsõk között tartozom köszönettel legközvetlenebb munkatársaimnak, Kálmán Erikának és Karl Heinziger professzornak, akikkel a pályám elejétõl kezdve a kutatás minden örömét és kudarcát együtt éltük át, és Márta Ferenc akadémikusnak, aki az utolsó 15 évben kutatásainkat lehetõvé tette, kutatási feltételeink megteremtését elõsegítette és a kutatásaimat ösztönözte.
Meleg köszönettel tartozom Hajdú Ferencnek, aki a tudományos pályára bevezetett, a kísérleti adatok kritikus analízisére nevelt és számos ötletével hozzájárult munkám eredményeihez. Köszönettel tartozom néhai Lengyel Sándor
professzornak, aki a folyadékdiffrakciós módszerek meghonosítását lehetõvé tette a 60-as, 70-es években és akinek a tématerületen megkezdett kutatásait folytathattam. Köszönettel tartozom Holló János akadémikusnak, korábbi igazgatómnak a támogatásáért.
Köszönettel tartozom Radnai Tamásnak és Philippe Boppnak, akikkel hosszú idõn keresztül számos probléma megoldásán együtt dolgoztunk.
Kegyelettel emlékszem Ruff Imre professzorra, kedves barátomra, akivel tudományos problémáimat megvitathattam és több megoldásán együtt dolgozhattam.
Külön köszönettel tartozom Vékony Ferencnek, akivel kutatásaink számos eredményének gyakorlati alkalmazását megvalósíthattuk.
Köszönettel tartozom tanítványaimnak, elsõsorban Bakó Imrének, továbbá többi közvetlen munkatársaimnak, hazai és külföldieknek egyaránt, akikkel kutatásaim különbözõ szakaszában együtt dolgoztam és, publikáltam és így vitathatatlan az elért eredményeimhez való hozzájárulásuk.
Köszönet illeti a kísérleti munkában hosszú idõn keresztül segítséget nyújtó munkatársaimat Haklik Lajost, Eke Annát, Tarlós Évát és Lukácsy Magdolnát.
Az elõadás témájához kapcsolódó publikációk
1. Hajdú F., Lengyel S., Pálinkás G.: X-ray scattering and radial distribution function of liquid water, J. Appl. Cryst., 9 134 (1976)
2. Pálinkás G., Kálmán E., Kovács P.: Experimental atom pair correlation functions of liquid heavy water, Mol.Phys., 34, 525 (1977)
3. Pálinkás G., Riede W.O., Heinzinger K.: Molecular dynamics study of aqueous solutions, Z.Naturforsch., 32a, 1137 (1977)
4. Pálinkás G.: Comments on the tetrahedral structure of water, Faraday Disc.Chem.Soc., 66, 147 (1978)
5. Szász Gy., Heinzinger K., Pálinkás G.: The structure of the hydration shell of the lithium ion, Chem.Phys.Lett., 78, 154 (1981)
6. Pálinkás G., Radnai T., Szász Gy., Heinzinger K.: The structure of an aqueous ammonium chloride solution, J. Chem.Phys., 74, 3522 (1981)
7. Pálinkás G., Radnai T., Dietz W., Heinzinger K.:
Hydration shell structures in MgCl2 solution form X-ray
and MD studies, Z.Naturforsch., 36a, 1076 (1982)
8. Pálinkás G., Bopp P., Jancsó G., Heinzinger
K.: The effect of pressure on the hydrogen bond structure of
liquid water, Z.Naturforsch., 39a, 179 (1984)
9. Pálinkás G., Heinzinger K.: Hydration shell structure of the calcium ion, Chem.Phys.Lett., 126, 251 (1986)
10. Pálinkás G., Hawlicka E., Heinzinger K.: A molecular dynamics study of liquid methanol with flexible three-site model, J.Phys.Chem., 91, 4334 (1987)
11. Pálinkás G., Tamura Y., Spohr E., Heinzinger K.: Molecular polarity and the structure of liquid methanol, Z .Naturforsch., 43a, 43 (1987)
11. Pálinkás G., Tamura Y., Spohr E., Heinzinger K.: Molecular polarity and the structure of liquid methanol, .Naturforsch., 43a, 43 (1987)
12 .Pálinkás G., Hawlicka E., Heinzinger K.: MD simulation of water-methanol mixtures, Chem.Phys., 158, 65 (1991)
13. Pálinkás G., Bakó I., Heinzinger K., Bopp P.: Molecular dynamics investigation of the inter and intra-molecular motions in liquid, methanol and methanol-water mixtures, Mol.Phys., 73, 897 (1991)
14. Pálinkás G., Bakó I.: Excess properties of methanol-water mixtures, Z.Naturforsch., 46a, 95 (1991)
15. Pálinkás G., Jedlovszky P.: Network of strongly interacting atoms in liquid argon, Chem.Phys., 185, 173 (1994)
16. Jedlovszky P., Bakó I., Pálinkás G.: Reverse Monte Carlo simulation of liquid water, Chem.Phys.Lett., 221, 183 (1994)
17. Bakó I., Pálinkás G., Heinzinger K.: X-ray diffraction study of methanol-water mixtures, Z.Naturforsch., 49a, 967 (1994)
18. Pálinkás G., Heinzinger K.: Ion solvation in methanol, ACH, Models in Chemistry, 132, 5 (1995)
Összefoglaló munkák
1. Pálinkás G., Kálmán E.:
Diffraction investigation of aqueous electrolyte solutions in Diffraction
Studies of Non-
Crystalline Substances, eds.: Hargittai I., Orville-Thomas Elsevier,
Amsterdam, Akadémia Kiadó, Budapest (1981)
2. Heinzinger K., Pálinkás G.: Computer simulation of ion-solvent systems, in The Chemical Physics of Solvation, Part A, eds.: Dogonadze R., Kálmán E., Kornysev A., Ulstrup J., Elsevier, Amsterdam, New York (1985)
3. Pálinkás G., Kálmán E.: X-ray, electron, and neutron diffraction studies of ionic solvation, in The Chemical Physics of Solvation, Part B, eds.: Dogonadze R., Kálmán E., Kornysev A., Ulstrup J., Elsevier, Amsterdam, New York (1986)
4. Heinzinger K., Pálinkás G.: Interactions of water in ionic hydrates, in Interactions of Water in Ionic and Non-ionic Hydrates, ed.: Kleeberg K. Springer Verlag, Berlin, Heidelberg (1987)
5. Spohr E., Pálinkás G.: Computer simulations
of water interactions near single crystal surfaces, in Interactions
of
Water in Ionic and Non--ionic Hydrates, ed.: Kleeberg K. Springer Verlag,
Berlin, Heidelberg (1987)
6. Pálinkás G., Heinzinger K.: Simulation of liquid mixtures, in Hydrogen Bond Networks, eds.: Bellissent-Funel M.C., Dore J. Kluwer Academic Publisher, (1994)