
Magyarfalvi Gábor
A molekulaszerkezet hatása az NMR árnyékolásokra (elméleti vizsgálatok)
Eötvös Loránd Tudományegyetem, Természettudományi Kar
1999
1. Bevezetés
A mágneses magrezonancia spektroszkópia a modern kémia leghatékonyabb szerkezetvizsgálati módszerei közé tartozik. Az eltolódás az NMR legalapvetõbb paramétere; egy spektrum megfejtését ma is az jelenti, hogy a különbözõ eltolódásokat a molekula atomjaihoz rendeljük. A tapasztalatok szerint nem túl nehéz a molekula szerkezete és az eltolódás között kapcsolatot találni. Az a priori számítások a kémiai szerkezetvizsgálat ezen területén is új lehetõségeket nyitnak. Szerepük nem egyszerûen a mérések reprodukálása. Komoly segítséget nyújthatnak a mérési eredmények, a tapasztalati szabályok értelmezésében. Kísérleti adatokkal párosítva igazolhatják a vizsgált anyagok szerkezetét. A számítások esetenként gyorsabbak, flexibilisebbek lehetnek a méréseknél, sõt kísérletileg el nem érhetõ szerkezetek is vizsgálhatóak. Egyszóval segítenek megérteni a molekulák geometriája, elektronszerkezete és mágneses tulajdonságai közötti összefüggéseket.
Különösen hasznosak lehetnek a számítások, amikor a kémiai eltolódást nem skalár, izotróp mennyiségként vizsgáljuk, hanem tenzorként. Az ilyen mérések még kevésbé elterjedtek a kémiai gyakorlatban, jóval kevesebb adat érhetõ csak el. Ezért sem olyan könnyû az eredmények értelmezése, hiába hordoz a tenzor több információt a vizsgált anyagról. Ezen a területen még több lehetõség van arra, hogy a számítások segítségével elõre jelezzünk, értelmezzünk, szabályokat állítsunk fel.
Az eltolódások kvantummechanikai elmélete gyakorlatilag
egyidõs az NMR spektroszkópiával. Ennek ellenére
a megbízható ab initio számítások
nagyobb molekulákra gyakorlatilag csak az utóbbi évtizedben
váltak lehetõvé. Dolgozatomban ilyen számításokról
és szerkezetvizsgálati alkalmazásukról számolok
be. Az alkalmazások közös motívuma az árnyékolási
paraméterek és a molekulageometria közötti kapcsolat
vizsgálata. Az elméleti bevezetést egy újszerû,
teljesen az alapoktól kiinduló gondolatmenetre építettem
fel. Az A függelékben kitérek a számítások
parallel számítógépekre történt
alkalmazására és néhány programszervezési
kérdésre. A B függelékben az árnyékolási
tenzorok szemléletes megjelenítésének módszereit
foglalom össze és teszek néhány tökéletesítési
javaslatot.
2. Háromtagú gyûrûk atomjainak árnyékolási anizotrópiája
A háromtagú gyûrûk elektronszerkezete már hosszú ideje foglalkoztatja a kémikusokat. A közelmúltban szilárd fázisú NMR méréseket végeztek szilíciumot is tartalmazó, háromtagú gyûrûs vegyületeken. A 29Si magokra mért árnyékolási anizotrópiát a szerzõk szokatlanul nagynak találták más szilíciumtartalmú vegyületekhez, illetve az analóg szénvegyületekhez képest. Azt kívántuk elméleti úton tanulmányozni, hogy a nagy anizotrópiát visszaadják-e a számítások, illetve azt, hogy ezek az értékek valamiféle különleges kötésszerkezetnek tulajdoníthatóak-e.
Az árnyékolások számítását a TX90 és a PQS programmal végeztem a GIAO-SCF módszert használva. A számítások jól reprodukálják az izotróp árnyékolásokat. A számítások segítségével megállapítható az árnyékolási tenzor fõtengelyeinek az iránya is. A nagy anizotrópiát egyértelmûen a gyûrû síkjára merõleges elem (szz) okozza.
A gyûrûre merõleges irányban tapasztalt nagy árnyékoltság értelmezéséhez a kérdéses vegyületekhez hasonló molekulákra is végeztünk számításokat. Azokban a vegyületekben, ahol szz közvetlenül összehasonlítható, ez a principális elem monoton növekszik, ahogy a Si–Si–X szög csökken. Sokat vizsgálták már az analóg vegyületek a feszülési energiáit. A végsõ következtetések szerint elsõdlegesen a szögfeszültség, a Baeyer-feszültség határozza meg ezeket. Lehetséges-e, hogy szz szokatlanul erõs árnyékoltságát is a gyûrût alkotó atom környezetének szokatlan geometriája okozza?
Természetesen a geometria, illetve a kötésrendszer hatását gyakorlatilag lehetetlen elválasztani egymástól. A következõ modellel mégis megkíséreltem a két tényezõ hatásának különválasztását. A TMS molekula egy C–Si–C szögét 60 és 116 fok közötti értékeken rögzítettem. A rendszer többi geometriai paraméterét megkötés nélkül SCF/3-21G* szinten optimáltam. A kapott torzult rendszerben számítottam ki a központi Si atom árnyékolását az SCF-GIAO módszert használva. Az erõsen eltorzított molekulák esetében is alapvetõen ugyanaz marad a molekula kötésrendszere, bár jóval magasabb az energiájuk, mint a normális szerkezetnek.
Az eredmények igazolják az elõzetes feltevést. Ahogy a rögzített szög csökken, a rá merõleges irányba tapasztalható árnyékolás és ennél fogva az árnyékolás anizotrópiája dramatikusan megnõ. Az ábra mutatja a tenzor változását a geometria torzulásával.

Ugyanezt a vizsgálatot a TMS molekulán felül a SiH4 és CH4 molekulára is elvégeztem. Ez is azt mutatja, hogy az anizotrópia a szokatlanul kis kötésszög folytán növekszik meg, attól függetlenül, hogy milyen atomok kapcsolódnak a központi maghoz.
A háromtagú gyûrûket alkotó atomok árnyékolása és anizotrópiája tehát nagyobb, mint a nyílt láncú vegyületekben, mert a gyûrû síkjára merõleges paramágneses árnyékolás kicsi. A jelenséget az okozza, hogy az atom környezetének geometriája eltorzul, nem pedig az, hogy a háromtagú gyûrûk kötésszerkezete valamilyen módon különleges lenne. A kis paramágneses árnyékolás azzal magyarázható, hogy a mágneses tér által a hullámfüggvényben okozott változásban más-más szimmetriájú gerjesztés dominál a tetraéderes és a 60 fokos geometria esetén.
Ezt a jelenséget a szilícium vegyületekben vizsgáltam
meg a legrészletesebben, de ugyanígy fellép szén,
illetve más atomok esetén. Ez magyarázatot ad arra
is, hogy mi okozza a háromtagú gyûrûk atomjainak
szokatlanul magas és anizotróp árnyékolását
3. Imidazo-tiazinok konformációjának vizsgálata
Az imidazo[2,1-b][1,3]-tiazin vázat tartalmazó vegyületek szintézisének új módszerét dolgozta ki Perjési Pál. A kapott termékek szerkezetét tömegspektroszkópiai, röntgendiffrakciós és NMR vizsgálatokkal igazolták. A különbözõképpen szubsztituált imidazo-tiazinok mindegyikének az NMR spektruma erõs oldószerfüggést mutatott. Ezt próbáltam számítások segítségével megmagyarázni.
Az összes megvizsgált vegyület NMR spektruma eltéréseket mutatott attól függõen, hogy deuterokloroformban vagy deutero-dimetil-szulfoxidban vették fel. Az effektus két oldószerben végzett mérések között a legnagyobb eltérés a tiazin gyûrûhöz közvetlenül kapcsolódó protonok NMR paramétereiben tapasztalható. Pl. a C(7)-hez tartozó proton 0,16 ppm-mel árnyékoltabb kloroformban. A két érintett proton között kloroformban a csatolás értéke 4,7 Hz, DMSO-ban 5,8 Hz-ra növekedik.
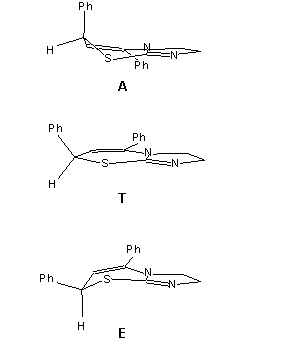
Azt feltételeztem, hogy az oldószer a molekula konformációs egyensúlyára van hatással. A meglehetõsen merev, sík geometriához közeli gyûrûrendszernek nincs sok módja konformációs változásra. Egyedül csak a hatos gyûrûnek van lehetõsége mozgásra két félszék jellegû elrendezõdés között. A szilárd fázisban a röntgendiffrakciós eredmények tanúsága szerint a C(7)-hez kapcsolódó fenil csoport kváziaxiális helyzetben van. Elképzelhetõ egy másik konformáció is, amelyben a fenilcsoport kváziekvatoriális helyzetbe kerül. Az ábra mutatja a két szerkezetet és izomerizációs folyamatuk átmeneti állapotát.
A két konformer H(6)--H(7) csatolási állandói között komoly különbségnek kell lennie, ugyanis a megfelelõ H–C(6)–C(7)–H torziós szög nagyot változik kettõjük közt. A kváziaxiális formában (A) ez a torzió kicsi, a két hidrogénatom nincs távol a fedõ helyzettõl. A kváziekvatoriális (E) alakban viszont a torzió 90 fok körül van, minthogy a C(7) hidrogénje axiális pozícióba kerül. Közel merõleges vicinális kötések általában nagyon kicsi csatolással járnak, így itt is az várható, hogy E csatolási állandója jóval kisebb lesz.
A konformációs változás hipotézisét
számításokkal ellenõriztük. Az elvégzett
HF ab initio számítások szerint az inverzió
energiagátja 6,54 kJ mol–1, tehát szobahõmérsékleten
a két konformer gyakorlatilag szabadon alakulhat át egymásba.
A eredmények azt mutatják, hogy vákuumban a kváziekvatoriális
szerkezet a stabilabb. A közel apoláris kloroform-oldatban
nem várható mélyreható változás
a számításokhoz képest, tehát feltételezhetjük,
hogy ebben az oldatban az E forma fog dominálni. A kváziekvatoriális
konformációban a H–C(6)–C(7)–H csatolás értéke
kicsi lesz. Az a tény, hogy ez a csatolás megnövekedik
a DMSO oldatban, arra utal, hogy a nagyobb csatolással rendelkezõ
A forma ott nagyobb súllyal járul a konformációs
egyensúlyhoz. Ezt a két konformerre végzett árnyékolási
számítások is megerõsítik. Az A
formát DMSO-ban valószínûleg a S atom jobb szolvatálhatósága
stabilizálja.
4. A sûrûségfunkcionál-elmélet segítségével számított árnyékolások empirikus korrekciója
Az utóbbi évtizedben egyre szélesebb alkalmazást nyer a kémiában is a sûrûségfunkcionál-elmélet (DFT – Density Functional Theory), amelynek a pontossága megközelítheti a korrelációs módszerekét, míg a számításigénye még a Hartree-Fock számításoknál is kisebb lehet. Az árnyékolások esetében a sûrûségfunkcionál-elméletet használó eljárások eddig még nem hoztak olyan pontos eredményeket, mint más mennyiségeknél. Sajnos az elmélet nem ad olyan nyilvánvaló technikákat a módszer javítására, mint az egyre összetettebb korrelációs módszerek használata a szokásos számításokban. Ezért kézenfekvõ megvizsgálni, hogyan lehet az eredményeket jobban összhangba hozni a mérésekkel.
Két magyarázatot is létezik a pontatlan eredményekre. Az egyik az, hogy a Hohenberg-Kohn tétel nem érvényes mágneses térbe helyezett molekulákra, ugyanis ilyenkor a rendszer energiája az elektronsûrûségen felül az elektronok áramsûrûségétõl is függ. A másik magyarázat szerint a perturbációs számításban használt virtuális pályák sajátértékei a funkcionál hibájából pontatlanok.
Malkin és munkatársai a virtuális pályák energiáinak korrekciójával javítani tudták a DFT módszerrel számított árnyékolások értékeit. A Malkin-féle korrekció többé-kevésbé empirikus, az eredmények hitelesítik, de nehéz változtatni rajta. Ezért érdemes volt egy folyamatosan hangolható korrekciót keresni, amellyel optimálni lehet az eredményeket és esetleg még tovább lehet javítani a számított árnyékolások pontosságát.
A legegyszerûbb módosítás az volt, hogy az összes virtuális pálya energiáját egy konstans értékkel megemeltük Az eljárás számításigénye éppen olyan alacsony lesz, mint az eredeti, csatolás nélküli DFT-nek. A számításokat a PQS programmal végeztük, amelyben a korrekcióval kiegészítve újraimplementáltam a TX93 GIAO-DFT modulját. Az optimális korrekciót GIAO-CCSD(T) árnyékolásokkal szemben kalibráltam a következõ molekulákon: CH4, CO, HCN, HF, H2O, NH3, N2 és F2.
A korrekció határozottan eredményesnek látszik. A virtuális pályák energiáinak megemelése az összes molekula esetében javít az ereményeken. Egészen meglepõ mértékben egyezik a szükséges korrekció mértéke teljesen más jellegû molekulák, mint pl. a dinitrogén és a metán esetében. Az optimális értékeknél szinte minden árnyékolás 5 ppm-nél közelebb kerül a CCSD(T) értékekhez, míg korrekció nélkül az eltérés 5–90 ppm között változik.
Ugyan a korrekció jó eredményeket ad a módszer
tesztelésére használt molekulákra, de mégis
az igazi próba az optimált korrekció alkalmazása
más molekulákra. A korrigált DFT árnyékolások
(BLYP funkcionál, TZP bázis, 0,025 hartree korrekció,
BLYP/TZP geometria) más molekulákban is jól reprodukálják
a méréseket. A táblázat a 77Se árnyékolásokra
kapott eredményeket tartalmaz.
| CPHF | MP2 | CCSD | BLYP | korr. | Mérés | |||
| 77Se árnyékolások | ||||||||
| SeH2 | 2178,5 | 2275,6 | 2213 | 2018,3 | 2128,1 | |||
| SeHCH3 | 2043,8 | 2093,0 | 1786,0 | 1928,1 | ||||
| Se(CH3)2 | 1927,0 | 1922,3 | 1878 | 1604,9 | 1778,9 | |||
| 77Se eltolódások | ||||||||
| SeH2 | –251,5 | –353,4 | –335 | –413,4 | –349,2 | –345,8 | ||
| SeHCH3 | –116,8 | –170,7 | –181,1 | –149,2 | –154,7 | |||
| Se(CH3) | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
Az eredmények azt mutatják, hogy a virtuális pályák
energiájának egyszerû, konstanssal való megemelése
határozottan javít a GIAO módszerrel számított
árnyékolásokon. Sõt az empirikusan meghatározott
optimum ugyanazon bázis és funkcionál mellett a molekulák
zömére átvihetõnek tûnik. Az eljárás
hatalmas elõnye az, hogy míg pontossága a korrelációs
módszerekkel vetekszik, de számításigénye
még az egyszerû CPHF-nél is kisebb. Az optimális
korrekció meghatározásához az itt bemutatott
vizsgálatoknál jóval szélesebb körben
kell tesztszámításokat végezni. Ez folyamatban
van.
5. Parallel ab initio számítások
A számítógépek rohamos fejlõdése már ab initio szinten is lehetõvé teszi sokatomos rendszerek számításokkal való vizsgálatát. Az elméleti kémikusok számításigénye azonban gyakorlatilag kielégíthetetlen, mindig akad nagyobb méretû érdekes molekula, potenciális-energiafelület. Hiába kétszerezõdik meg néhány évente a számítógépek teljesítménye, a cél mindig az marad, hogy csökkentsük a számítások idõigényét, persze a költségeket ésszerû határok között tartva.
A személyi számítógépek ár/teljesítmény
arányának drasztikus csökkenése szinte tálcán
kínálta a lehetõséget arra, hogy PC-k összekapcsolásával
olyan olcsó, házi “szupergépet” építsünk,
ami eléri a kereskedelmi munkaállomás-csoportok teljesítményét
a költségek tört része mellett. Ezt a tervet valósítottuk
meg, ami persze a számításainkban használt
program komoly áttervezését is szükségessé
tette. Ebben az átalakításban vettem részt,
ezt dokumentálja ez a függelék. Az átalakításban
használt elvi megfontolásokat és a megvalósítás
technikai részleteit is ismertetem. A dolgozatban említett
számítások egy részét is a program párhuzamos
változatával végeztem, részben a magunk építette,
részben pedig kereskedelmi párhuzamos számítógépeken.
6. Az árnyékolási tenzorok szemléletes megjelenítése
Az árnyékolási tenzorok értelmezésében sokat segíthet, ha szemléletesen, grafikusan jelenítjük meg az általuk hordozott információt. Több módszer is létezik a tenzorok ábrázolására, egy részüket alkalmazták már árnyékolási tenzorokra is. Ebben a függelékben megpróbálom áttekinteni és értékelni a lehetõségeket, helyenként javítva és bõvítve a megjelenítés szemléletességén; eközben a gyakorlati megvalósítás részleteire is kitérek.
A legegyszerûbb, de talán leghasznosabb ábrázolás a tenzorok ORTEP stílusú ellipszoidjainak megjelenítése, ugyanis az árnyékolási tenzorok ellipszoidjait egybõl a molekulageometriával együtt látjuk. Az ábrán (ld. angol nyelvû Ph.D. thesis) a hexametil-ciklotriszilán molekula számított árnyékolásait rajzoltam fel.
NMR shieldings and molecular structure (ab initio studies)
Ph.D. Thesis, Eötvös Loránd University, Budapest
1999
1. Introduction
Nuclear magnetic resonance spectroscopy is one of the most efficient tools of modern chemistry. The chemical shift is its most fundamental parameter. Solving a structure by NMR amounts to assign the shifts to the atoms of the molecule. It proved to be easy to find correlation between molecular structure and chemical shifts. A priori calculations open up new possibilities in this respect. Their role is more than the reproduction of experiments. They help to understand results and trends. Together with measurements they can prove structures. Occasionally they can be faster and more flexible than experiments. They can even produce results not available by measurements. Altogether they help to understand the connection between molecular and electronic structure and magnetic properties.
Calculations are especially useful when we study the anisotropic, tensorial properties of the chemical shift. Such experiment are less widespread, less experience has been accumulated. Thus the interpretation of the results is more difficult, even if the tensor carries more information about the structure. This field offers lots of possibilities for prediction and interpretation.
The quantum mechanical theory of the chemical shift is almost as old
as NMR itself. However, reliable ab initio calculations for bigger
molecules are the product of the last decade. This thesis reports such
calculations and their applications in structural studies. The common element
in the applications is the study of the correlation between molecular geometry
and shielding parameters. The theoretical part is presented using a new
derivation. Appendix A describes the methods used for the implementation
of the calculations on parallel computers. Appendix B discusses methods
for visualization of shielding tensors.
2. Shielding anisotropy in three-membered rings
The electronic structure of three-membered rings has long been a subject of discussion. Recently solid-phase NMR measurements were done on silicon containing three-membered rings. The authors found the 29Si shielding anisotropy to be unusually high compared to other silicon compounds and the analogous carbon compounds. We wanted to find out whether these anomalous values can be reproduced and whether they can be
Shielding calculations were done using the TX90 and PQS program and the GIAO-CPHF method. Isotropic shielding were reproduced quite well. Calculations enabled the determination of the orientation of the shielding tensor. High anisotropies are caused by the principal element perpendicular to the plane of the ring (szz).
We carried out calculations on similar compounds to interpret the high shielding in the perpendicular direction. In the molecules where szz can directly be compared this element was increasing as the Si–Si–X angle was decreasing. The strain in analogous rings was found to depend mostly on the angle. Can the unusual shielding of szz be attributed to the unusual geometry in the vicinity of the ring atoms?
Obviously the effects of geometry and bonding can not be completely separated. The following model still tries to differentiate between the two. One angle in a TMS molecule was fixed at a value between 60 and 116 degrees. Other geometrical parameters were optimized at the HF/3-21G* level. The shielding of the central Si atom was calculated using the GIAO-CPHF method.
The results agree with the hypothesis. As the fixed angle is decreased, the shielding in the perpendicular direction and the shielding anisotropy increases dramatically. The figure shows the change in the tensor components with the angle.
The same calculations were done on SiH4 and CH4 molecules with results showing that the unusually low bond angle causes the increase in anisotropy independently of the atoms in the molecule.
The shielding and anisotropy of the atoms in three-membered rings is higher than the similar values in open chains, because the paramagnetic shielding perpendicular to the ring is very low. This phenomenon is caused by the distorted geometry of the atoms. The low paramagnetic shielding can be explained by the fact that the change of the molecular wavefunction caused by the magnetic field is dominated by excitations of different symmetry in different structures.

This phenomenon was studied in detail using silicon compounds, but it
can be observed on carbon and other atoms as well. Thus we have found a
general explanation for the high shielding and anisotropy of three-membered
rings.
3. Study of the conformations of imidazo-thiazines
A new method for the synthesis of imidazo[2,1-b][1,3]-thiazine rings was developed by Perjési Pál. The structure of the products obtained was proved by NMR, MS and X-ray studies. All imidazo-thiazines showed strong solvent dependence in NMR. I tried to find an explanation using calculations.
All compounds gave a different spectrum in deutero-chloroform and deutero-dimethyl-sulfoxide. The effect was highest for the protons directly attached to the thiazine ring. E.g. the proton on C(7) was 0.16 ppm more shielded in chloroform. The coupling between the two protons in question was 4.7 Hz in chloroform as opposed to 5.8 Hz in DMSO.
We supposed that the solvent brings about a change in the conformational equilibrium of the molecule. The rigid, almost planar ring system does not have much possibility for movement. Only the six-membered ring can have two half-chair type conformations. The phenyl group on C(7) is in a quasi-axial position in the solid phase as shown by the X-ray measurements. Another form, where the phenyl group is in a quasi-axial position is also possible. The figure shows the two structures and the transition state of their isomerisation.

The H(6)–H(7) coupling constant must be different in the two conformers,
as the H–C(6)–C(7)–H torsional angle changes drastically between the two
forms. In the quasi-axial form (A) this angle is quite low, the
two hydrogens are almost in a staggered position. In the quasi-equatorial
form (E) this angle is almost 90 degrees. Thus we can expect a distinctly
lower coupling constant for this case.
The hypothesis of conformational change was checked by calculations.
The HF ab initio results gave a value of 6,54
kJ mol–1 for the energy barrier of the inversion. That means
practically free conversion between the two conformers at room temperature.
The quasi-equatorial structure was shown to be more stable in vacuum.
We can suppose that in the almost apolar chloroform solution the equilibrium
is dominated by this form. This way the H–C(6)–C(7)–H coupling is low as
expected. The increase of the coupling in DMSO shows that the A
form contributes more to the equilibrium. This is also supported by the
shieldings calculated for the two forms. The A form is probably
stabilized by the better solvability of the S atom.
4. Empirical correction for shielding calculated by density functional theory
Density functional theory (DFT) was applied widely for chemical problems in the last decade. Its accuracy can get close to correlational methods, while its computational cost can be lower than HF calculations. DFT shielding calculations were less accurate so far. Unfortunately the theory does not provide obvious ways to improve on the method as the better and better correlational techniques improve in traditional quantum chemistry. Thus it was necessary to find other ways to bring calculations and measurements in accordance.
There are two explanations for the inaccuracy of the results. On one hand the Hohenberg-Kohn theorem is not valid for molecules in magnetic field, as the energy of the system is a functional of the current density in addition to the electron density. The other explanation says that the eigenvalues of the virtual orbitals used in the perturbational treatment are in error due to the inaccurate functionals.
Malkin and coworkers could improve the DFT shielding values using a correction of the energies of the virtual orbitals. Their correction is more or less empirical and hard to change. Thus we set out to find a continuously tunable correction. Thus the results can be optimized and possibly improved further.
The simplest change was to increase the energy of all virtuals by the same value. The method has the same, low computational cost as the uncoupled DFT. The calculations were done by the PQS program, in which I had implemented the GIAO-DFT module. The optimal correction was calibrated against GIAO-CCSD(T) shieldings on the following molecules: CH4, CO, HCN, HF, H2O, NH3, N2 and F2.
The correction seems to bring an improvement for all systems studied. It is quite surprising how different molecules, such as methane and nitrogen require the same value of correction. The optimum brings all shieldings within 5 ppm of the CCSD(T) values, while differences of the uncorrected results are in the 5–90 ppm range.
The real test of the method is the application of the optimum correction
on molecules not included in the test set. The corrected DFT shieldings
(BLYP functional, TZP basis, 0,025 hartree correction, BLYP/TZP geometry)
reproduce experiments quite well. The table contains 77Se shielding
results.
|
|
CPHF | MP2 | CCSD | BLYP | corr. | Exp. | ||
| 77Se shieldings | ||||||||
| SeH2 | 2178,5 | 2275,6 | 2213 | 2018,3 | 2128,1 | |||
| SeHCH3 | 2043,8 | 2093,0 | 1786,0 | 1928,1 | ||||
| Se(CH3)2 | 1927,0 | 1922,3 | 1878 | 1604,9 | 1778,9 | |||
| 77Se shifts | ||||||||
| SeH2 | –251,5 | –353,4 | –335 | –413,4 | –349,2 | –345,8 | ||
| SeHCH3 | –116,8 | –170,7 | –181,1 | –149,2 | –154,7 | |||
| Se(CH3) | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
A simple, constant increase in the energy of the virtual orbitals is
a distinct improvement of GIAO-DFT shielding. The correction seems to be
highly transferable at the same functional and basis. The biggest advantage
of the method is that its computational cost is lower than the simple HF
method, while its accuracy is close to correlational methods. Further and
wider testing of the method is in progress.
5. Parallel ab initio calculations
The fast development of computing made ab initio studies possible for multiatom systems. However, the computing needs of theoretical chemists can not practically be satisfied. There is always a bigger interesting molecule, potential energy surface. Even with the speed of computers doubling in every few years, faster calculations at a reasonable price will always be an aim.
The drastic reduction in the price/performance ratio of personal computers
provided a favorable opportunity for us to build inexpensive, homemade
“supercomputers” by connecting PCs. These machines attain the power of
commercial workstation clusters at a fraction of their price. The implementation
of this plan made the redesign of our program necessary. This appendix
documents my contributions to this project. Design concepts and technical
details are included. Parts of the calculations mentioned earlier were
done by the parallel version of the code.
6. Visualization of shielding tensors
The interpretation of shielding tensors can be facilitated if their information content is visually presented. There are many methods to present tensors; some were even applied for shieldings. This appendix presents and evaluates the possibilities improving and extending them.
The simplest, but potentially most useful method is the ORTEP style drawing of the tensors as the ellipsoids are presented together with the molecular geometry. The figure shows the shieldings of hexamethyl-cyclotrisilane.

Publications
1. G. Magyarfalvi and P. Pulay : "Ab initio calculation of selenium-77
NMR shieldings", Chem. Phys, Letters, 225 (1994), 280
2. G. Magyarfalvi and P. Pulay: "Chemical shift anisotropies in silicon-containing
three-membered rings - an ab initio study", Chem. Phys. Letters,
241 (1995), 393
3. P. Perjési, P. Sohár, Zs. Böcskei, G. Magyarfalvi,
Ö. Farkas, M. Mák: "Synthesis, structure and conformational
analysis of imidazo-thiazines", J. Mol. Struct., 377 (1996) 277
4. K. Süvegh, A. Domján, G. Magyarfalvi, Gy. Vankó,
A. Vértes: "Hydrogen-bonded clusters in aqueous solutions: a combined
positron annihilation and FTIR study", Material Science Forum, 255-57
(1997), 348-350
| Vissza a tartalomjegyzékhez
Back to Contents |
http://www.kfki.hu/chemonet/
http://www.ch.bme.hu/chemonet/ |