The 8-bit inspiration vol 3: Plus/4 assembly XORSHIFT generator for dummies

The C code (from here) reads:

/* 16-bit xorshift PRNG */

unsigned xs = 1;

unsigned xorshift( )
{
    xs ^= xs << 7;
    xs ^= xs >> 9;
    xs ^= xs << 8;
    return xs;
}

Let's see how the steps of this algorithm look like. It is a 16 bit generator, so we have two bytes; h stands for "high", l stands for low. The operator "^=" is an XOR operation; << and >> are left and right bit shifts, respectively. So the steps are as follows:

   x x x x x x x x |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8|x x x x x x x x
   x h1h2h3h4h5h6h7|h8l1l2l3l4l5l6l7|l80 0 0 0 0 0 0 |x x x x x x x x
XOR------------------------------------------------------------------
                    i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8

The i-s form a new byte, and m1 is the first bit of the new low byte; note that XOR-ing with 0-s is the identity operation, so apart from the first bit, the rest of the lower byte is untouched.

   x x x x x x x x |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8|x x x x x x x x
   x x x x x x x x |0 0 0 0 0 0 0 0 |0 m1l2l3l4l5l6l7|l8x x x x x x x
XOR------------------------------------------------------------------
                    i1i2i3i4i5i6i7i8|m1n2n3n4n5n6n7n8

In this step we leave the high byte and the first bit of the low byte untouched; the nontrivial part is the rest of the low byte.

   x x x x x x x x |i1i2i3i4i5i6i7i8|m1n2n3n4n5n6n7n8|x x x x x x x x
   i1i2i3i4i5i6i7i8|m1n2n3n4n5n6n7n8|0 0 0 0 0 0 0 0 |x x x x x x x x
XOR------------------------------------------------------------------
                    o1o2o3o4o5o6o7o9|m1n2n3n4n5n6n7n8

In this step the low byte is not touched anymore.

For the 8 bit implementation one should note that in each step the XOR is applied to single bytes only; this makes is suitable for the 8-bit implementation.

We have the two bytes in two memory addressess: $H and $L. We can operate on the AC register and we have an additional carry bit, we can do XOR's between the AC and memory addresses; this instruction is called EOR. In addition we can shift single bits. For this we shall use 2 instructions which work in this way:

LSR

    AC              |carry  
    a1a2a3a4a5a6a7a8|c
LSR 0 a1a2a3a4a5a6a7|a8

ROR

    AC              |carry  
    a1a2a3a4a5a6a7a8|c
ROR c a1a2a3a4a5a6a7|a8

First I quote the code I had found here, it is said that this should be doing the same as the C code on the 16 bits represented by rng_zp_high and rng_zp_low:

random
LDA rng_zp_high
LSR
LDA rng_zp_low
ROR
EOR rng_zp_high
STA rng_zp_high ; high part of x ^= x << 7 done
ROR ; A has now x >> 9 and high bit comes from low byte
EOR rng_zp_low
STA rng_zp_low ; x ^= x >> 9 and the low part of x ^= x << 7 done
EOR rng_zp_high
STA rng_zp_high ; x ^= x << 8 done
RTS

Let's understand how the algorithm works step by step. At a point we shall depart from it though.

1. Read $H to the AC

       AC              |carry  |$H              |$L      
       x x x x x x x x |x      |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8
LDA $H-----------------------------------------------------------
       h1h2h3h4h5h6h7h8|x      |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8

1. Apply LSR to AC

       AC              |carry  |$H              |$L      
       h1h2h3h4h5h6h7h8|x      |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8
LSR    ----------------------------------------------------------
       0 h1h2h3h4h5h6h7|h8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8

The first two steps were done to realize a single goal: to have h8 in the carry; its use will be clear in step 4.

1. Load $L to AC

       AC              |carry  |$H              |$L      
       0 h1h2h3h4h5h6h7|h8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8
LDA $L ----------------------------------------------------------
       l1l2l3l4l5l6l7l8|h8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8

1. Apply ROR

       AC              |carry  |$H              |$L      
       l1l2l3l4l5l6l7l8|h8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8
ROR    ----------------------------------------------------------
       h8l1l2l3l4l5l6l7|l8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8

As you can see now we have in AC the very thing the high byte has to be XOR-ed with in Step 1 of the C code. So let's XOR the AC with $H:

1. Apply EOR

       AC              |carry  |$H              |$L      
       h8l1l2l3l4l5l6l7|l8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8
EOR $H ----------------------------------------------------------
       i1i2i3i4i5i6i7i8|l8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8

1. Store the high byte after the frist step.

       AC              |carry  |$H              |$L      
       i1i2i3i4i5i6i7i8|l8     |h1h2h3h4h5h6h7h8|l1l2l3l4l5l6l7l8
STA $H ----------------------------------------------------------
       i1i2i3i4i5i6i7i8|l8     |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8

It is not a problem that we've lost h1… h8 from now on; we do not need them anymore. Flippin'eck, we are at the 6th step, and we have done only the first half of the first step of the 3 of the algorithm. This illustrates why I prefer C over assembly… Anyway, let's proceed.

7? Apply ROR (WRONG)

       AC              |carry  |$H              |$L      
       i1i2i3i4i5i6i7i8|l8     |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8
ROR    ----------------------------------------------------------
       l8i1i2i3i4i5i6i7|i8     |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8

This would be the next step according to the code from the forum. But now what? Note that the first bit of AC is l8 which has to be XOR-ed with l1 in the first step of the C algorithm; this can be done with EOR $L to calculate m1=l1 XOR l8. Meanwhile the description says "AC has now x >> 9 and high bit comes from low byte". The second half of the statement we have recognized, but how does AC have x>>9? He must mean that after l8 we should have m1l2l3l4l5l6l7, but come on, we have i1i2i3i4i5i6i7. We will have m1 only after the XOR.

Actually someone in a comment at the page did say afterwards that the Z80 code the guy had ported was incorrect, too, and indeed, it seems that it is. So let's try and fix it…

Looking at the first step of the C code, we have the I-s, but we are in the need of m1, this we have to calculate as the second step needs it as an input.

7: Zero out AC

         AC              |carry  |$H              |$L      
	 i1i2i3i4i5i6i7i8|l8     |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8
LDA #$00 ----------------------------------------------------------
         0 0 0 0 0 0 0 0 |l8     |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8

8: Get l8 to the first bit of AC:

         AC              |carry  |$H              |$L      
         0 0 0 0 0 0 0 0 |l8     |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8
ROR      ----------------------------------------------------------
         l80 0 0 0 0 0 0 |0      |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8

8: Calculate m1 as the first bit of AC and get the rest of $L to AC

         AC              |carry  |$H              |$L      
         l80 0 0 0 0 0 0 |0      |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8
EOR $L   ----------------------------------------------------------
         m1l2l3l4l5l6l7l8|0      |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8

Note that the EOR with 0 is actually the identity:

0 EOR 0 = 0
0 EOR 1 = 1

thus we got the copy of l2 at the right place. So the first step of the C code is almost done; we just need to store the result:

         AC              |carry  |$H              |$L      
         m1l2l3l4l5l6l7l8|0      |i1i2i3i4i5i6i7i8|l1l2l3l4l5l6l7l8
STA $L   ----------------------------------------------------------
         m1l2l3l4l5l6l7l8|0      |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8

Hurray, ready for step 2 of the C code.

1. Shift AC

         AC              |carry  |$H              |$L      
         m1l2l3l4l5l6l7l8|0      |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8
LSR      ----------------------------------------------------------
         0 m1l2l3l4l5l6l7|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8

Note that in the present situation ROR would have done the same.

1. Do step 2 of the C code

         AC              |carry  |$H              |$L      
         0 m1l2l3l4l5l6l7|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8
EOR $L   ----------------------------------------------------------
         m1n2n3n4n5n6n7n8|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8

1. Store the final lower byte

         AC              |carry  |$H              |$L      
         m1n2n3n4n5n6n7n8|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8
STA $L   ----------------------------------------------------------
         m1n2n3n4n5n6n7n8|l8     |i1i2i3i4i5i6i7i8|m1n2n3n4n5n6n7n8

1. Do the last step of the C code

Luckily our AC is just ready for this:

         AC              |carry  |$H              |$L      
         m1n2n3n4n5n6n7n8|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8
EOR $H   ----------------------------------------------------------
         o1o2o3o4o5o6o7o9|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8

1. Store the final result's high byte

         AC              |carry  |$H              |$L      
         o1o2o3o4o5o6o7o9|l8     |i1i2i3i4i5i6i7i8|m1l2l3l4l5l6l7l8
STA $H   ----------------------------------------------------------
         o1o2o3o4o5o6o7o9|l8     |o1o2o3o4o5o6o7o9|m1l2l3l4l5l6l7l8

And it is done. When iterating, AC and the carry shall be initialized anyway so it is not a problem that we leave some rubbish there.

Our final code thus reads, in a TEDMON-compatible fasion, assuming that the low bit is at $3000 and the high bit is at $3001:

A 2000 LDA $3001
       LSR
       LDA $3000
       ROR
       EOR $3001
       STA $3001
       LDA #$00
       ROR
       EOR $3000
       STA $3000
       LSR
       EOR $3000
       STA $3000
       EOR $3001
       STA $3001
       RTS
       JSR $2000
       BRK

Here it is how it looks like as I type it in TEDMON (in the emulator for the time being):

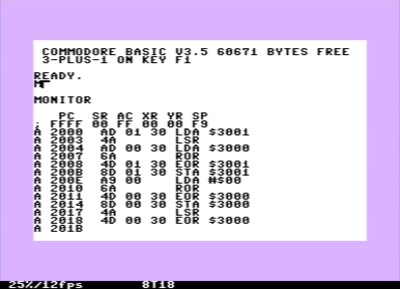
and here is the complete listing:

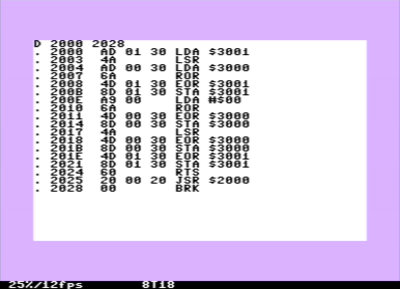
We thus have our iteration subroutine at 2000, so after seeding we can do iterations with G 2025, which is the last but one line that is a small main program calling the iteration once.

The command M 3000 3001 can be used for looking at the two bytes as well as seeding; here it is how it looks like:

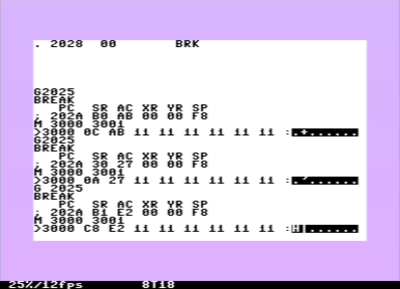
It seems to work indeed. I hope that it is correct now.

What next? I shall surely sit to my real Plus/4 to try it there, too. After all, this is my first nontrivial assembly code for the Plus/4 some 32 years after my first attempt. I don't easily give up my dreams. It would be nice now to have some plot in the screen on the basis of these random bytes, that will be the next project probably.

But frankly even though it was fun to implement this and there were lessons to learn, I wouldn't say I became a great fan of Assembly. I appreciate highly that we do have high-level languages and one can write efficient codes in them. If I consider the real-life problems I'm solving nowadays, if I were to solve them in Assembly, well… It is nice to think back to the good old days but I'd not go back.