Máthé Sándor

nyugalmazott középiskolai tanár
az Eötvös Loránd Fizikai Társulat tagja

Az eleai Zénon mintegy kétezerötszáz éve fedte fel a mozgás ellentmondásosságát, amely arra épül, hogy az euklideszi geometria szerint a pontnak nincs kiterjedése. A kilõtt nyílvesszõ pontról pontra kell haladjon, de a pontnak nem lévén kiterjedése, tehát el sem indulhat. A tapasztalat az ellenkezõjét igazolja, tehát el kellene fogadjuk, hogy a nyílvesszõ áll is és mozog is. Filozófiai disputák máig sem vezettek eredményre, s a kérdés megoldatlan maradt. Azonban a fizikában fizikai konstansokból természetes úton meg lehet határozni egy kiterjedéssel rendelkezõ pontot. A megoldás nyitját ott kell keresni, hogy a fogalmak nincsenek kellõen tisztázva, a nyelv logikai szerkezete nem kielégítõ [ 1 ].

Már Heisenberg felhívta a figyelmet arra, hogy a sebességnek csak két pont között, az energiának pedig egy T idõintervallumban van értelme. Sebesség egy adott idõpillanatban értelmetlen.

Max Planck fizikai konstansok segítségével tömeget, hosszúságot és idõintervallumot határozott meg amelyeknek reális értelmezést adhatunk.

Létezik egy olyan kicsi m tömeg amelynek gravitációs hossza R_g (a Schwarzschild sugár fele) egyenlõ a hozzátartozó Compton hullámhosszal [2], [3].

és az - bõl kapjuk
, ahol Planck tömeg

Az m-et a 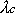-be helyettesítve az u.n. Planck hosszúságot kapjuk

továbbá idõperiódusra

A keresett fizikai pont P^* amit kvantum pontnak nevezhetünk, -t véve helyett gravitációs térre. Térbeli pontra P_s*

Belátható, hogy a fizikai pont értéke spin fiiggõ. A Planck relációkat általánosíthatjuk: létezik olyan M makrotömeg amelynek R_ggravitációs hossza egyenlõ, egy m mikrotömeg Compton hullámhosszával. Az alábbi relációkat kapjuk:

továbbá

Nevezzük m-et az M korrelatívjának és fordítva. Ez utóbbi relációk ahhoz segítenek, hogy minden makrotestre felírt fizikai relációt m hullámtermészetû mikrorészecskére írhatjuk át.

Újabb bõvítést eszközölhetünk. Létezik olyan m_e mikrorészecske amelynek gravitációs tömege ekvivalens az elemi e villamos töltéssel (például elektron vagy proton töltése).

Megjegyzendõ, hogy finomszerkezeti állandó.

Felírhatók az alábbi relációk:

Az egy újabb fizikai pontot ad négy fizikai konstans segítségével. Megjegyzendõ, hogy az így meghatározott fizikai pontok és idõ intervallumok irracionális számokkal fejezhetõk ki. Ugyanakkor mint elemi kvantumok egész számokat képviselnek. Másképpen szólva ha lemondunk arról, hogy a nyílvesszõ egyidõben áll is és mozog is, akkor el kell fogadjuk, hogy a helymeghatározó pontok egyszerre lehetnek racionális (egész számok) és irracionális számokk al kifejezve. A fizika tehát egy új számelmélet kidolgozását igényelné.

[ 1 ] Wittgenstein, Tractatus Logico-Philozophicus, 1922

[2] Robert M. Wald, General relativity, pp. 470-471 on Units and Dimensions (University of Chicago Press, Chicago, 1984)

[3] Jefferson Hane Waever, The World of Physics, vol., III., pp. 596-613 on The Cosmic Numbers (Simon and Schuster, New York, 1987)