|
Kezdőlap-Home
Page |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
III. évfolyam 1. szám
[HUN] - Magyar cikk
|
3.fejezet.....
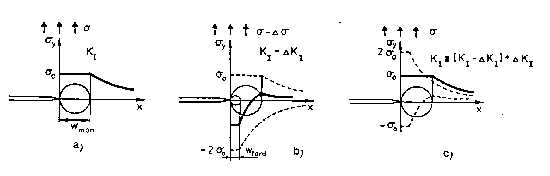
4. A kisciklusú fáradás és a fáradásos repedésterjedés közötti kapcsolat A különböző anyagok viselkedését, tulajdonságait azok minősége (összetétele, a kémiai kötések típusa, az atomok térbeli elrendeződése, mikro- és makroszerkezete), továbbá az alakváltozás sebessége, a hőmérséklet és a feszültségállapot befolyásolja. E sok tényező hatásának következménye, hogy az anyagok viselkedésének leírására nem rendelkezünk általános modellel, a tulajdonságok jellemzésére egész sor mérőszámot vagyunk kénytelenek használni. Ha terhelések lehetséges spektrumából kiemeljük a fárasztó igénybevételt, akkor is több anyagi mérőszámot kell meghatározni ahhoz, hogy a méretezéshez, az ellenőrzéshez alapadatot szolgáltassunk. Más jellemzőket határozunk meg a kisciklusú, s a nagyciklusú fáradásnál vagy a fáradásos repedésterjedésnél. Felvetődik tehát a kérdés, hogy - egy ilyen viszonylag szűk területen - találhatók-e olyan közös mechanikai, anyagszerkezeti sajátosságok, amelyekre építve az anyagi mérőszámok között kapcsolat tételezhető fel? 4.1. A mechanikai állapot összehasonlítása Kisciklusú fárasztásnál a próbatest terhelése leggyakrabban olyan nagy, hogy már az első felterhelésnél, az első ciklusban, a próbatest vizsgálati szakaszának teljes térfogata képlékeny alakváltozást szenved [26]. A vizsgálatok többségénél a vezérelt változó a teljes alakváltozás amplitúdó (ea) [24], amelynek időbeli változása rendszerint szinusz vagy háromszög függvény szerinti. Mivel a képlékeny alakváltozás tartományában nem lineáris a feszültség és az alakváltozás között a kapcsolat, a teljes alakváltozás amplitúdóra vezérelt kisciklusú fárasztásnál a feszültség időbeli változása az anyag viselkedésétől is függ. A 6. ábra ea=±1%-os teljes alakváltozás amplitúdójú kisciklusú fárasztásra mutatja az alakváltozás amplitúdó és a feszültségamplitúdó időbeli változását, amin jól látható a függvények különbözősége. Amennyiben a próbatest vizsgálati szakasza hengeres, a befogása egytengelyű, a vizsgált keresztmetszetek minden pontjában azonos tengelyirányú feszültség ébred. Fáradásos repedésterjedésnél a repedés csúcsában nemcsak a feszültség, hanem a feszültségintenzitási tényező (K), a képlékeny zóna mérete, a repedés szétnyílása és még számos paraméter ismétlődően, folyamatosan változik. Különbség lesz a monoton és a ciklikus terhelés keltette feszültségállapot között, ami a repedés csúcsában kialakuló képlékeny zónával van összefüggésben. A fáradásos repedésterjedési vizsgálatnál az első húzó terhelés során a repedés csúcsában egy képlékeny zóna keletkezik, amelynek maximális mérete függ az anyag folyáshatárától és a feszültségintenzitási tényező nagyságától. Ideálisan rugalmas-képlékeny anyagot és s, illetve s - Ds feszültséghatárok közötti feszültségváltozást feltételezve a maximális húzó terhelés hatására a 25. a) ábra szerinti y irányú feszültségkomponens eloszlás alakul ki a repedés csúcstól mért távolság függvényében. A képlékeny zónában fellépő maximális feszültség a folyáshatárral (s0) egyezik meg. A terhelés csökkenésével változik a feszültségeloszlás, amely s - Ds terhelésnél a s és a -Ds állapot szuperpozíciójának eredményeként határozható meg (25. b) ábra). Látható, hogy van egy olyan zóna, amelyben a sy feszültségkomponens nyomó, s - Ds húzó terhelés esetén is [86]. Ez a fordított képlékeny zóna (wford). A következő húzó terhelési ciklusnál a feszültségeloszlás a s - Ds és a +Ds állapot szuperpozíciójával hozható létre (25. c) ábra), és az első húzó terhelési ciklusra jellemző állapot áll elő [28]. A fel- és leterhelések ismétlésével a kisciklusú fárasztáshoz hasonló feszültségváltozás következik be, de a képlékeny zónában ténylegesen fellépő, valós aszimmetria tényező a s és a Ds viszonyától is függ. Az előző gondolatsor alapján nyilvánvaló, hogy a fáradásos repedésterjedési vizsgálatoknál az anyag igénybevétele hasonlít a kisciklusú fárasztó vizsgálatéhoz.
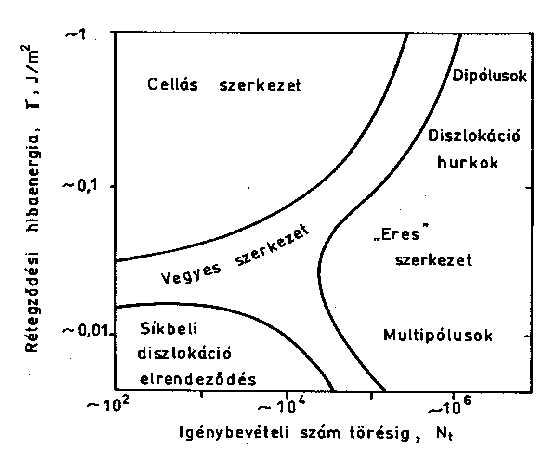
25. ábra: Feszültségeloszlás a fárasztott próbatest repedésének csúcsában 4.2. A diszlokációs szerkezet összehasonlítása Az egyensúlyi állapothoz közeli, lágy fémekre és ötvözetekre a viszonylag kis diszlokáció-sűrűség és az egyenletes diszlokáció eloszlás jellemző [87]. A fárasztás hatására nő a diszlokáció-sűrűség, jelentkezik a diszlokációk egyenlőtlen eloszlása is. Kezdetben az átlagos diszlokáció-sűrűség intenzíven nő az igénybevételi szám növekedésével, majd tart egy maximumhoz, aminek értéke a terhelési amplitúdó növekedésével nő. A képlékeny alakváltozás a diszlokációk mozgásával jár együtt, ami a terhelés jellegéből következően váltakozó irányú lesz, mértéke pedig az igénybevétel nagyságától - vagy ami ezzel analóg - a tönkremenetelig elviselt ciklusszámtól függ. Az igénybevételi szám és a vele együtt járó diszlokáció sokszorozódás, a változó irányú diszlokációmozgás következtében előtérbe kerülnek a diszlokációreakciók, és ezzel a diszlokáció blokkolódások. A további alakváltozás a diszlokációkat az akadályok kikerülésére készteti, ami megfelelő keresztcsúszási képesség esetén lehetséges is [88]. Ez elvezet a diszlokációk térbeli rendeződéséhez, ami az igénybevétel nagyságától és a keresztcsúszási képességtől függ (26. ábra). A diagram mennyiségileg csak homogén feszültségállapot esetén, egyfázisú, felületen középpontos köbös fémekre és ötvözetekre, szobahőmérsékleten érvényes. Azon fémeknél és ötvözeteknél, amelyeknél a rétegződési hibaenergia nem határozható meg, a diagram minőségi jellemzést ad. Az előző diagram alapján a nagy igénybevételi amplitúdók (kis törésig elviselt ciklusszámok) esetén a rétegződési hibaenergia nagyságától függően két diszlokációs szerkezet fordulhat elő. Nagy rétegződési hibaenergia esetén a diszlokáció-sűrűség növekedésével együtt már az első ciklusokban jellemző az egyenlőtlen diszlokáció eloszlás is. Az éldiszlokációk, diszlokáció hurkok és dipólusok, nehezen mozgó diszlokáció részek kezdetben kondenzálatlan, elmosódott cellafalakat alkotnak. Az igénybevételi szám növekedésével nő a multipólusok száma, a falak diszlokáció-sűrűsége, a cellafal és a mátrix egyre határozottabban elkülönül [28, 89]. A cellák mérete a ciklusszám növekedésével kezdetben csökken, majd a telítődési állapot elérését követően már nem változik. A mátrix síkjainak orientációkülönbsége a cellafal két oldalán a fárasztás teljes ideje alatt növekszik [90]. A cellaméret fordítottan arányos az alakváltozás amplitúdóval [91], vagy a telítődési feszültséggel [90]. Egy tipikus cellás szerkezetről készült transzmissziós elektronmikroszkópi felvételt mutat a 27. ábra [92].
26. ábra: Tipikus diszlokációs szerkezetek az igénybevételi szám és a rétegződési hibaenergia függvényében
27. ábra: Fárasztás során keletkezett jellegzetes cellás szerkezet Amennyiben a rétegződési hibaenergia kicsi, keresztcsúszásra nem, vagy csak nagyon korlátozottan kerülhet sor. Mivel a diszlokációk nem tudják elhagyni elsődleges csúszási síkjukat, nem tudnak cellafalakat létrehozni [28, 91]. Ennek következtében a diszlokációs szerkezet tipikus síkbeli elrendeződést mutat. A technikai életben használatos fémek és ötvözetek kisciklusú fárasztóvizsgálata során döntő többségben cellás szerkezet alakul ki. A fáradásos repedésterjedés esetén a repedés előtti képlékeny zónában rendkívül nagy, helyi képlékeny alakváltozás következik be, bár mértéke a zóna egyes pontjaiban eltérő. A jelentős képlékeny alakváltozás hatására nagy rétegződési hibaenergia esetén cellás szerkezet alakul ki [93, 94, 95]. A cellák mérete a repedés közelében rendkívül kicsi, attól távolodva növekszik. Az egymás melletti cellák síkjainak orientáció különbsége is a repedés közelében a legnagyobb, attól távolodva az orientáció különbség csökken [96]. Kis rétegződési hibaenergiájú anyagok esetén a cellás szerkezet kialakulásának lehetősége rendkívül korlátozott, ezért cellákat csak a képlékeny zóna repedéshez közeli környezetében figyeltek meg [97]. Az előzőek alapján megállapítható, hogy a fáradásos repedésterjedésnél a repedés környezetében keletkező diszlokációs szerkezet nagymértékben hasonlít a kisciklusú fárasztás során kialakuló diszlokációs szerkezethez, egyfázisú felületen középpontos köbös fémek és ötvözetek esetén. Annak következtében, hogy a rétegződési hibaenergia, illetve a keresztcsúszási képesség az egyes ötvözettípusuknál eltérő, a diszlokációs szerkezet mennyiségi jellemzői különböznek, a képlékeny alakváltozás során lejátszódó diszlokációs folyamatok viszont hasonlónak tekinthetők. A műszaki életben nemcsak egyfázisú ötvözeteket használnak, ezért a fáradásnak kitett alkatrészek diszlokációs szerkezete, illetve a fáradás során bekövetkező diszlokációs szerkezet megváltozása is különbözhet az ötvözet állapotától, mikroszerkezetétől függően. Feltéve, hogy az eltérő diszlokációs szerkezetű többfázisú ötvözetek kisciklusú fárasztása és fáradásos repedésterjedése során hasonló a diszlokációs szerkezet megváltozása, miként azt az egyfázisú felületen középpontos köbös ötvözeteknél megfigyelhető volt, az várható, hogy a vonatkozó mérőszámok között kapcsolat létezhet. Ez a kapcsolat ötvözetcsoportonként és azok különböző állapota, mikroszerkezete esetén más és más lesz. 4.3. Vizsgálatok és eredményeik A vizsgálatokhoz három különböző ötvözetcsoportba (acél, alumíniumötvözet, szuperötvözet) tartozó, különböző állapotú anyagminőségeket használtunk fel. Az acélok egyik csoportját különböző mikroötvözött, másik csoportját pedig termomechanikusan kezelt minőségek alkották: 37C, KL7D, DX52, illetve X80TM, QStE690TM/StE690. Az alumíniumötvözetek közül – mikroszerkezetük alapján – az AlMg3, AlMg5.1Mn/AlMg5 és az AlMg4.5Mn minőségeket soroltuk az egyik csoportba, míg a 7076-T6 jelű ötvözet egy másik csoportot reprezentál, egyenlőre egyedül. Az elemzésbe bevont szuperötvözet a Waspaloy volt. A különböző anyagminőségek mechanikai tulajdonságait a 9. táblázatban foglaltuk össze. A kisciklusú fárasztóvizsgálatokat teljes alakváltozás amplitúdóra (ea) vezérelve, szobahőmérsékleten, levegőn végeztük. Az alakváltozást átmérőmérővel mértük, a terhelési függvény időbeli változása szinuszos volt. A fárasztás aszimmetria tényezőjét R=-1-re, a tönkremeneteli ciklusszámot a maximális húzóerő 25 %-os csökkenésére választottuk. A vizsgálat során regisztráltuk a teljes alakváltozás és feszültségamplitúdók maximális és minimális értékét, valamint a hiszterézis hurkokat. 9. táblázat: A vizsgált anyagminőségek mechanikai tulajdonságai
A vizsgálati eredményeket az általánosan elterjedt formában dolgoztuk fel [26], vagyis meghatároztuk a
alakú Manson-Coffin egyenlet paramétereit. Az egyes anyagminőségekre meghatározott c értékeket az 10. táblázatban foglaltuk össze. 10. táblázat: A Manson-Coffin és a Paris-Erdogan összefüggések paraméterei
A fáradásos repedésterjedési sebesség vizsgálatokra CT, illetve TPB próbatesteken [98], szobahőmérsékleten és levegőn, szinusz alakú terhelési függvény szerint, R=0,1-es terhelés aszimmetria tényezővel került sor. A repedés méretét optikai, illetve reciprok rugóállandó (compliance) módszerrel mértük. A vizsgálat során gyűjtött, illetve feljegyzett adatokból meghatároztuk a Paris-Erdogan összefüggés állandóit, az egyedi eredmények ismeretében pedig számítottuk az 5-26 próbatesten mért adatok átlagát. A meghatározott jellemzőket – hasonlóan a kisciklusú fárasztóvizsgálatok eredményeihez – az 10. táblázatban tüntettük fel. A hipotézis ellenőrzésére végzett – a saját vizsgálatok jelentős idő és gépigénye miatt – az adatokat irodalomból származó mérési eredményekkel is kiegészítettük. Ez valószínűleg növeli a rendelkezésre álló statisztikai minták bizonytalanságát, mert azonos anyagminőség esetén is jelenős különbségek lehetnek a vizsgált anyagi mérőszámokban az egyes adagok tulajdonságaiban meglévő eltérések miatt. Növelheti a bizonytalanságot az is, hogy a különböző országokban és/vagy a különböző gyártóknál előállított ötvözetek tulajdonságai eltérőek lehetnek. Végül az óhatatlanul meglévő vizsgálattechnikai különbségek is eredményezhetnek nagyobb szórásokat. Mindezek ellenére indokolt és szükséges irodalmi adatok felhasználása, mert csak kellő számú mérési eredmény esetén van lehetőség az összetett kérdéskör megválaszolására. 4.4. Az eredmények értékelése
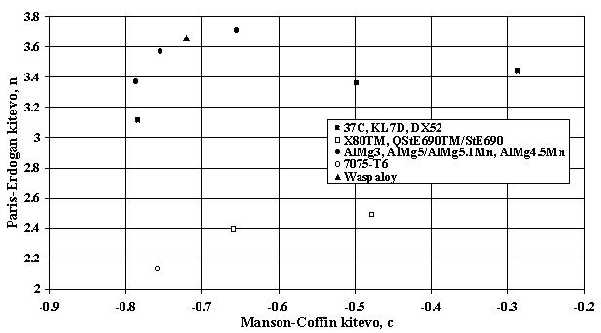
28. ábra: Kapcsolat a Manson-Coffin és a Paris-Erdogan összefüggés kitevői között A viszonylag kevés mérési adat ellenére megállapítható, hogy a kisciklusú fáradásra jellemző Manson-Coffin és a fáradásos repedésterjedési sebességet leíró Paris-Erdogan összefüggés kitevői között elfogadható kapcsolat van mikroötvözött, növelt folyáshatású acéloknál és alakítható alumíniumötvözeteknél. E két kapcsolat, az ötvözettípusok különbözősége miatt eltérő. Két adatpár alapján külön csoportba tartozóknak kell tekinteni a nagyszilárdságú, termomechanikusan kezelt acélokat (X80TM, QStE690TM) és egy újabb halmaz előfutára a nemesített alumíniumötvözetre (7075-T6) vonatkozó pont. Az eltérés magyarázata a első esetben a termomechanikus kezelés hatására kialakuló, az egyensúlyitól távol lévő diszlokációs szerkezet, a másodikban pedig a kiválásosan keményített alumíniumötvözet precipitátumai és a diszlokációk között kialakuló – a lágy állapothoz képest eltérő – kölcsönhatás. Nyilvánvalóan külön csoportba tartozóak lesznek a szuperötvözetek, egyetlen adat azonban még nem elégséges következtetések megfogalmazására.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||