 |
 |
|
5. ábra |
6. ábra |
Molekuláris oldatkémia
A rácsmodellektõl a molekuladinamikai konfigurációkig
Pálinkás Gábor
a Magyar Tudományos Akadémia levelezõ
tagja
A 60-as években az oldatkémia egyik központi kérdése volt a víz szerkezetének a kérdése. Bár mindenki számára világos volt, hogy általában a folyadékállapotot rövidtávú rendezettség és hosszú távú rendezetlenség uralja, a víz számos anomális tulajdonságai olyan konfliktust okoztak, amelyek akadályozták a két jellemzõ közti, a rövidtávú rend és a hosszú távú rendezetlenség közti átmenet megértését.
Az egyik ilyen anomális tulajdonság a víz olvadáskor lejátszódó sûrûségnövekedése. Különös az is, hogy a folyadékállapot kiterjedt hõmérséklet-tartományon létezik. Ez hosszú távú erõk jelenlétét sugallta. Igen kicsi a jég olvadáshõje, ez csupán 15%-a a párolgáshõnek. Figyelemreméltó a víz kis kompresszibilitása is. A kompresszibilitás a repulziv erõk mértéke. Talán a víz leganomálisabb tulajdonsága a nagy hõkapacitása, amely mintegy felére csökken mind olvadáskor, mind forráskor.
Ezek az anomális tulajdonságok mind azt sugallták, hogy a víz hosszabb távú rendezettséget örökölt a szilárd fázistól, mint a többi folyadék. Ezt a gondolatot tükrözte a hatvanas években kidolgozott nagyszámú szerkezeti modell mindegyike. A modellek egy részletes összefoglalója található Erdey-Grúz Tibor 1971-ben megjelent könyvében. A számosságuk ellenére az akkori szerkezeti modelleknek volt néhány közös eleme: Az egyik ilyen vonás volt az, hogy rövid távon, de néhány száz szomszédra kiterjedõen kisebb, vagy nagyobb mértékben megõrizzék a jég valamely módosulatának rendezett tetraéderes szimmetriájú szerkezetét és a rendezetlenséget a jól rendezett térfogatrészek, klaszterek közötti elszakadt hidrogénkötésekkel képzelték el.
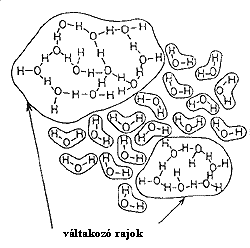
Ilyen volt az 5.ábrán látható a folyadék egész térfogatára kiterjedõ rácsmodell. A rácsból kiszakadt és a jégrács csatornáiban elhelyezkedõ vízmolekulák, az u.n. rácsközi vízmolekulák és a hibahelyek jelentették a rendezetlenség megjelenését a modellben. Ilyenek voltak a klasztermodellek is, amelyekben a végsõe méretû néhányszáz molekulára kiterjedõ, a jég valamely módosulatának szimmetriájával rendelkezõ, klaszterek közötti, elszakadt hidrogénkötések és a klaszterek felületéhez közel elhelyezkedõ molekulák csökkenõ hosszú távú rendezettsége jelentette a rendezetlenség megjelenését a vízben.
 |
 |
|
5. ábra |
6. ábra |
Említésre érdemes még Némethy és Scherraga váltakozó rajok modellje magyar vonatkozása miatt, de azért is, mert talán ez a modell áll legközelebb a jelenleg általánosan elfogadott modellekhez (6.ábra). Ebben a klasztermodellben a vízmolekulák közvetlen környezetére a tetraéderes szimmetria nem volt jellemzõ. Bár a klaszterekben domináns volt a molekulák négy hidrogénkötése, 3 illetve 2 hidrogénkötéssel rendelkezõ molekulák is elõfordultak a klaszterek belsejében. A váltakozó méretû rajok a monomerek tengerében úsztak. Erre a modellre is jellemzõ volt a kétállapotú vízmolekula, a kötött és szabad vízmolekulák elõfordulása.
Bár elképzeléseink a víz szerkezetérõl az elmúlt negyedszázad alatt megváltoztak, a rácsmodellek tudományos jelentõségét nem szabad lebecsülnünk. Kísérleti tényekre épültek és egy egy anomális tulajdonságot kvantitatív magyarázni lehetett segítségükkel. Az elszakadt hidrogénkötés fogalma is kísérleti spektroszkópiai tényre épült..
Az 7. ábrán a víz infravörös OH nyújtási sávjának differenciaspektrumát láthatjuk a hõmérséklet függvényében a 10 oC hõmérsékleten felvett sávhoz viszonyítva. A jégben a rezgés sávja 3200 cm-1-nél jelenik meg, a gõzfázisú molekula sávja 3755 cm-1 hullámszámnál jelentkezik. A molekula nyújtási rezgéseinek sávjában gõz-folyadék fázisátmenetkor elõálló vöröseltolódás jellemzõje a hidrogénhidas folyadékoknak. Folyadékállapotban alacsony hõmérsékleten a sáv helye 3300 cm-1 , de nagyfrekvenciás oldalán egy váll figyelhetõ meg. A hõmérséklet növelésével a nagyfrekvenciás járulék intenzitása nõ, a kisfrekvenciásé csökken. Ennek a ténynek a magyarázatára épült számos kétállapotú vízmodell és épült az elszakadt hidrogénkötések fogalma. Itt kell megemlítenem, hogy az oldószer említett sávjai nemcsak a hõmérséklet hatására tolódnak el, de megfigyelhetõ a jelenség oldott anyagok hatására is, amely effektus alapozott meg olyan fogalmakat, mint az ionok szerkezetépítõ és romboló hatása.
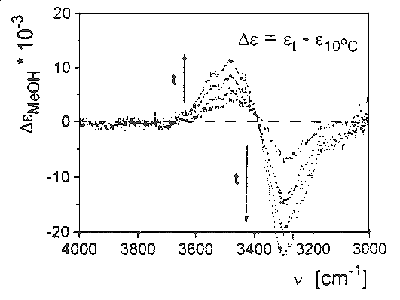
7. ábra
A spektrum intenzitásváltozásának analízisével egyszerû becslés volt tehetõ az elszakadt hidrogénkötések számára, a szabad vízmolekulák mólarányára. Ezen becslés szerint a szabad molekulák száma növekszik a hõmérséklet növekedésével, 0–100 oC fok között, azonban az ilyen molekulák száma még a víz forráspontján sem haladja meg a molekulák 20%-át.
Elektrolitoldatok korai modelljeire az volt jellemzõ, hogy az oldószert kontinuumként kezelték. Ilyen volt a hidratáció Born-féle modellje, vagy az elektrolitoldatok Debye–Hückel-modellje, vagy az oldatok olyan rácsmodelldelljei, melyekben az ionok oldatban egy köbös relaxált rács pontjaiban helyezkedtek el a kontinuum oldószerben.
Ezidõtájt foglalkoztatta intenzíven az irodalmat az ionok osztályozása pozitívan-negatívan hidratálókra vagy szerkezetromboló és szerkezetépítõ ionokra aszerint, hogy az oldószer valamely tulajdonsága a nagyobb, vagy alacsonyabb hõmérsékleteken felvett értéke felé tolódott el az ionok hatására. Értelmezve az effektust azzal, hogy bizonyos ionok rendezettebbé, más ionok rendezetlenebbé teszik az oldószer szerkezetét a tiszta oldószerhez képest. Ezek a fogalmak rosszul definiáltak voltak, mindegyik szerzõ mást értett a fogalmak alatt. Ma már világos, hogy a nevezett fogalmak ellentmondásosak és mindkét hatás egyidejûleg lejátszódik a vizes elektrolitoldatokban.
Változást jelentettek a modellezésben a hatvanas évek végén megindult számítógépes szimulációk a Monte-Carlo és molekuladinamikai számítások. A hatvanas évek végén és a hetvenes évek elején Rahman és Stillinger megjelentette a víz szerkezetének és dinamikájának elsõ molekuladinamikai számításait és K. Heinzinger Németországban 1973-ban elkezdte tömény vizes elektrolitoldatok molekuladinamikai számításait.
1975 volt az az év, amikor magam is bekapcsolódtam az elektrolitoldatok molekuladinamikai modellezésébe K. Heinzinger meghívására, amely meghívást azért kaptam, hogy a diffrakciós kísérleti adataink alapján pontosítsuk a molekuladinamikai számításokat.
A számítógépes szimulációs módszerek elterjedése, a determinisztikus molekuladinamikai és a sztochasztikus Monte-Carlo számítások eredményei, továbbá a folyadékdiffrakciós módszerek fejlõdése szemléletváltozást hoztak létre a modellezésben. Úgy gondolom, hogy a két területen végzett munkánk eredményei hozzájárultak az említett szemléletváltozáshoz.
Az említett szemléletváltozásnak két fontos eleme van. Az egyik annak a meggyõzõdésnek a megerõsödése, hogy nincs elvi különbség az intermolekuláris és a kémiai kötést létrehozó erõk között, a másik pedig az, hogy a folyadékokban a rendezetlenség lokálisan, már a molekulák közvetlen környezetében megjelenik, az intermolekuláris kötés geometriája torzult. Az intermolekuláris erõk forrása is lényegében a molekulák, illetve fragmenseiknek Coulomb-kölcsönhatása. Az intermolekuláris kölcsönhatások három fontos típusa – a van der Waals kohézió, a hidrogénkötés, az elektronpár donor-akceptor kötés – közül talán a két utóbbi specifikus kölcsönhatás jellemzõi között ismerhetõ fel legjobban a kémiai kötés két markáns attribútuma, az irányítottság és a sztöchiometrikus jelleg. A munkánk egyik fontos tárgyát képzõ hidrogénhíd-kölcsönhatás egy rövidtávú molekulafragmensekre lokalizált kohéziós erõ, amely perturbálja a partnerek kémiai kötését. A hidrogénkötés a donor protonja és az akceptor magános elektronpárja közötti kölcsönhatás. Az erõsségét a donor pillératomjának elektronegativitása, irányítottságát az elektronpár molekulapályája, sztöchiometriáját az akceptor magános elektronpárjainak száma határozza meg. A hidrogénkötés energiája (10-40 kJ mol-1) nagyságrendben a kémiai kötés energiája (H2 436 kJ mol-1) és a van der Waals kohéziós energiák (1-2 kJ mol-1) között áll. Az A-H...B hidrogénkötésben a proton és a B akceptor távolsága van der Waals sugaraik összegénél rövidebb, az A-H kémiai kötés megnyúlik, rezgési frekvenciája vöröseltolódást szenved a perturbáció hatására.
A modern felfogás szerint a kémiai és intermolekuláris kötés minõségi hasonlósága alapján beszélhetünk az intermolekuláris kötés geometriájáról, átlagos kötéstávolságról, kötésszögrõl és rezgési amplitúdóról vagy a kötés élettartamáról. A kötés rezgési amplitúdója (0.01-0.04 nm) és élettartama (0.1ps-2ns) azok a jellemzõk, amelyeknek nagysága megkülönbözteti az intermolekuláris kötést a kémiai kötéstõl. A folyadékok intermolekuláris kötései által szervezõdõ molekulahalmazok egészének átlagos geometriája azonban már nem értelmezhetõ a halmaz elemeinek hõmozgás okozta nagy amplitúdójú torziós mozgásai miatt. A szupramolekuláris szervezõdésnek, a szupramolekuláknak geometriai leírását a molekulahalmazok egyidejû kötései által kifeszített hálók átlagos topológiai jellemzése helyettesíti. A kötéshálókat változékonyság jellemzi, méretük fluktuál, elemeik cserélõdnek. A folyadékszerkezet geometriai modelljeit statisztikus modellek váltották fel.
Az oldószerek és oldatok molekuladinamikai modelljei minõségileg eltérnek a korábbi oldatkémiai modellektõl abban, hogy a kölcsönhatásokat, a szerkezetet és a dinamikát egységesen modellezik, dinamikus modellek. A modell alapjaiban a molekulák kölcsönhatása áll és ebbõl levezeti a rendszer összes tulajdonságát. Ez a levezetés a mai napig folyik és az oldatok újabb és újabb tulajdonságai, egyensúlyi és nemegyensúlyi válnaik számíthatóvá a kölcsönhatási energiákra alapozva. A molekuladinamika egy igen nagyszerû vonása, hogy a molekulák trajektóriáinak mozgásállapotának mindenkori ismeretében a jelenségek összefüggése szemléletessé, a molekulák láthatóvá tehetõk a számítógép segítségével, amint erre késõbb példát is fogunk látni.
Néhány szót magáról a molekuladinamikai módszerrõl.
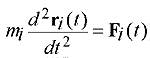 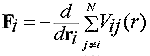 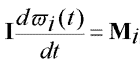  8. ábra |
A molekuladinamikai szimulációk lényege elvileg igen egyszerû: A folyadék kiválasztott térfogatrészében a sûrûsége által meghatározott számú molekulát kölcsönhatási energiafüggvényekkel látunk el, és megoldjuk minden molekula klasszikus mozgásegyenleteit a többi által létrehozott potenciáltérben egy kis dt idõre elõre (8.ábra). A dt értékét úgy kell megválasztanunk, hogy ez kisebb legyen a rendszerben elõforduló és tanulmányozni kívánt leggyorsabb mozgás karakterisztikus idejénél, és amely alatt feltételezlezhetõ, hogy a többi részecske potenciáltere állandónak tekinthetõ. Általában a dt idõlépés femtosecundum nagyságrendû vagy ennél kisebb, ha flexibilis belsõ erõkkel rezgésre késztetett molekulamodellekkel dolgozunk. Így elõáll a rendszer dt idõközönkénti konfigurációinak sokasága. Számosságuk 50000 és a több millió között lehet. Ezen a sokaságon a statisztikus fizika módszereivel a tulajdonságok különbözõ tér- és idõátlagát, vagy idõfüggését is meghatározhatjuk.
A határfeltételek megválasztásával a vizsgált rendszer modellezésének alapjául a molekulák különbözõ statisztikus sokaságát választhatjuk.
Különbözõ szellemes számítástechnikai módszerek léteznek a határfeltételek megvalósítására. Végezhetjük a szimulációt állandó összes energia, térfogat és részecskekeszám mellett, biztosíthatjuk az állandó hõmérsékletet, nyomást vagy kémiai potenciált is.
 9. ábra |
Felmerül a kérdés, mekkora legyen a kiválasztott térfogatrész, hány molekula trajektóriáját határozzuk meg? A modell molekuláinak számát felülrõl minden esetben a számítástechnikai lehetõségek korlátozzák. Mindenestre úgy kell megválasztanunk a modellrendszer méretét és a trajektóriák idõbeli kiterjedtségét, hogy azok nagyobbak legyenek a részecskék korrelációs hosszánál, illetve a vizsgálni kívánt mozgás karekterisztikus idejénél.
A modellek részecskeszáma jelenleg 200-1000 között mozog, ami megfelel 2-3 nm oldalélû kocka alakú térfogatnak és a számított molekulatrajektóriák hossza meghaladja 100-200 ps-ot. Kicsi a rendszer, rövid az idõ? Számításokkal kimutatható, hogy számos szerkezeti és dinamikai tulajdonság pontos számításához elegendõ, vannak azonban tulajdonságok, amelyek számításához nem elegendõ.
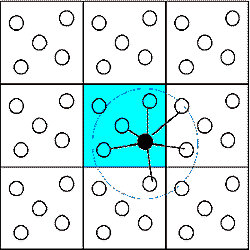
A kis méret miatt és falhatás elkerülésére a számításokat periodikus határfeltételek között végezzük. Ezt úgy érjük el, hogy a központi térfogatrészt minden irányban tükörképeivel vesszük körbe és a központi térfogatrészben elhelyezkedõ bármely molekula azonos sugarú gömbön belüli részecskék potenciálterében mozog falhatás nélkül (9.ábra).
| Klasszikus vagy kvantummechanika? | ||
Szerkezet 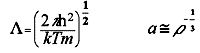 |
||
| folyadék | T1(K) | L/a |
| H2 | 14.0 | 0.97 |
| Ne | 24.5 | 0.26 |
| H2O | 273.2 | 0.08 |
| CH4 | 90.7 | 0.12 |
| N2 | 63.3 | 0.11 |
| Ar | 84.0 | 0.08 |
| Na | 371.0 | 0.05 |
| Kr | 116.6 | 0.05 |
| Dinamika |
||
| 10. ábra | ||
Másik kérdés: helyes-e, hogy klasszikus mechanikát használunk a rendszer trajektóriáinak elõállítására (10.ábra)? Szerkezeti tulajdonságok esetében erre a kérdésre a Broglie-hullámhossz és a molekulák karekterisztikus távolságának hányadosa alapján válaszolhatunk. Ha ez a hányados kisebb mint egy, a rendszer jó közelítésben klasszikusnak tekinthetõ. Látható, hogy a hidrogén, hélium és talán a neon kivételével az oldatkémiában szerepet játszó folyadékok jó közelítésben klasszikusnak tekinthetõk. A mozgásformák klasszikus vagy kvantum jellegének eldöntéséhez a termális energia Planck állandóhoz mért viszonyát kell vizsgálnunk. Ez a hányados szobahõmérsékleten 2.5. 10-14 szekundum értéket vesz fel. A folyadék molekuláinak transzlációs és rotációs karakterisztikus karakterisztikus idõi ennél az értéknél 2 nagyságrenddel nagyobbak. A vízmolekula OH nyújtási rezgésének periódusideje azonban 10-14 sec. Tehát flexibilis, rezgõ molekulamodellek használata esetén a klasszikus számítást sok esetben kvantumkorrekcióval kell ellátni. Ez meg is történik például akkor, ha a víz, vagy metanol belsõ energiájának és fajhõjének vibrációs járulékait számítjuk ki.
Néhány szót szeretnék még szólni a molekulamodellekrõl.
A számításokban biztosíthatjuk az egyensúlyi molekulageometriát merev kényszerekkel. Mód van arra is, hogy megengedjük a molekulageometria deformációját is, és szimuláljuk a molekula belsõ rezgéseit is. A molekula egyensúlyi geometriája körüli rezgéseket belsõ harmonikus vagy anharmonikus erõk modellezésével állítjuk elõ. Az erõállandók gázfázisú spektroszkópiai mérések normálkoorordináta analízisébõl származnak. Ilyen molekulamodelleket használtunk a késõbb bemutatandó víz, metanol és víz-metanol elegyek számításai során. Bár flexibilis molekulamodellek használata számítástechnikai nehézségeket jelent, nagy elõnyük, hogy segítségükkel az oldószer molekulák vibrációs spektruma is számítható és tanulmányozható például az oldott anyagok, ionok hatása is a spektrumra.
Következô rész
Vissza a tartalomjegyzékhez