 |
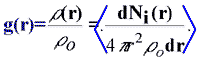 |
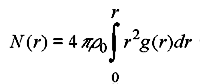 |
Molekuláris oldatkémia
A rácsmodellektõl a molekuladinamikai konfigurációkig
Pálinkás Gábor
a Magyar Tudományos Akadémia levelezõ
tagja
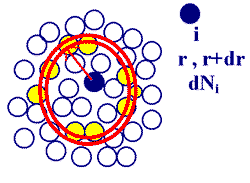
A páreloszlás függvények számítása a generált molekula konfigurációk sokaságán egyszerû számítástechnikai feladat (11. ábra). Egyszerûen megszámoljuk a részecskék adott tátávolságban elõforduló szomszédainak számát minden lehetséges részecskepár típusra. Ezeket a számokat átlagoljuk az összes konfigurációra, ezzel elõállt a pársûrûségek részecske- és idõátlaga.
 |
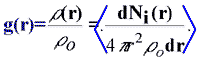 |
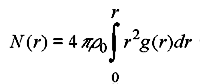 |
11. ábra
A molekulák dinamikájának számítása,
mint említettem, idõkorrelációs függvények
segítségével történik (12.ábra).
Az idõkorrelációs függvényének
Fourier-transzformáltja megadja a dinamikai tulajdonság spektrális
eloszlását. Tipikus példája az idõkorrelációs
függvényeknek a sebesség autokorrelációs
függvény.
| Dinamika
intramolekuláris rezgések |
 |
| autokorrelációs függvények spektrális eloszlás sebesség autokorrelációs függvény 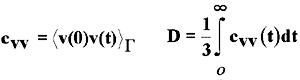 |
|
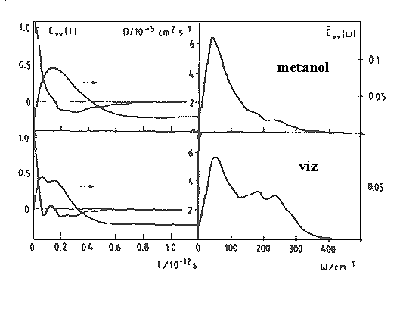
| 12. ábra | 13. ábra |
A transzlációs szabadsági fokok autókorrelációs függvényéhez jutunk ha a molekula tömegközéppontja sebességvektorának idõkorrelációs függvényét állítjuk elõ. A molekula öndiffúziós állandóját a Green-Kubo reláció alapján az autókorrelációs függvény idõ szerinti integrálja határozza meg. A sebesség autókorrelációs függvény Fourier-transzformáltja eredményezi a molekula transzlációs spektrumát, amely infravörös kísérleti adatokkal hasonlítható össze. A (13.ábra) a metanol- és vízmolekulák sebesség autokorrelációs függvényeit és transzlációs mozgásuk spektrumait mutatja be 3:1 víz-metanol elegyben szobahõmérsékleten végzett molekuladinamikai számítások alapján.
Rezgõ molekulamodellel végzett szimuláció esetén közelítõ normálkoordinátákat rögzítve a molekulához elõállíthatjuk a normálkoordináták sebesség autókorrelációs függvényeit és a vízmolekula szimmetrikus/antiszimmetrikus nyújtási és hajlítási rezgéseinek spektrumát a modellben (14.ábra, metanol).
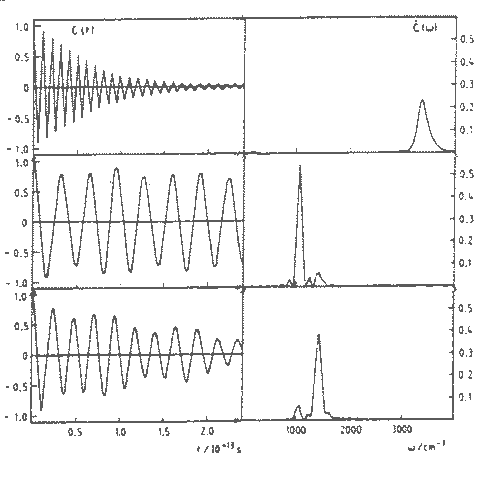
14. ábra
Korábban említettem, hogy a molekuladinamika egyik felmérhetetlen elõnye dinamikus jellege. A másik az, hogy az átlagos, kísérletekkel összehasonlítható tulajdonságok számítása mellett, a koordináták és sebességek mindenkori ismeretében, a számított rendszerek molekuláinak a kísérlet által nem, vagy csak pontatlanul mérhetõ egyedi tulajdonságai is számíthatóak. Így például megkülönböztethetõek kationok, anionok hidrátszférájában vagy a tömbfázisban elhelyezkedõ vízmolekulák és ezek járulékai egy adott tulajdonsághoz, de megkülönböztethetõek például metanolban láncközi, láncvégi vagy monomer, hidrogénkötést nem alkotó molekulák is. Egyedi iontulajdonságok számításának minõségére mutat be példát a (15.ábra), amelyen egy- és kétértékû ionok hidratációs energiáit tüntetjüki fel saját molekuladinamikai számításaink alapján (O) összehasonlítva azokat a kísérleti adatokkal (*) és a Born-modell alapján számított értékekkel (–).
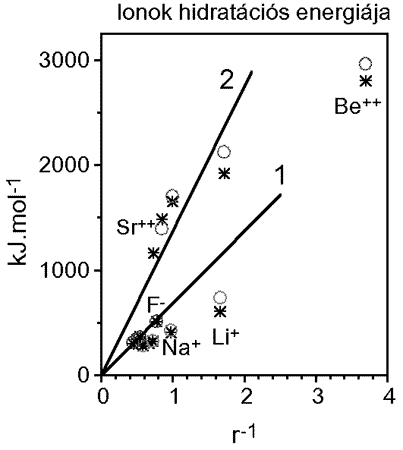
15. ábra
Következô rész
Vissza a tartalomjegyzékhez