|
Kezdőlap-Home
Page |
|||||||||||||||||||||||||||||||||
|
II. évfolyam 4. szám 2001. október
[HUN] - Magyar cikk
|
Modellezés és szimuláció az Anyagtudományban és az Anyagtechnológiákban
Dr. Tisza Miklós - Dr. Fülöp Tibor -
Adorján Gábor – Dr. Kiss Antal
Miskolci Egyetem
1. Bevezetés Az anyagtechnológiák (a képlékenyalakítás, a hegesztés és a hőkezelés) a gyártástechnológiában a legszélesebb körben alkalmazott eljárások közé tartoznak. Az anyagtechnológiák gyűjtőnév alkalmazását az egyes eljárások közös vonásai indokolják, alkalmazásuk ugyanis számos esetben azonos ismeretek, közel azonos technológiai adatbázis meglétét feltételezi. A sikeres technológiai folyamattervezéshez elsősorban ismerni kell az alkalmazott anyagok tulajdonságait, anyagjellemzőit. Ez egy anyagtudományi feladat megoldását igényli. Rendszerint fontos feladat a munkadarabot terhelő erőhatások, a szerszámterhelések meghatározása, illetőleg a mechanikai anyagjellemzők esetleges megváltozásának előrejelzése: ez egy műszaki mechanikai feladat megoldását igényli. Az előzőkön túl, az egyes technológiáknak a lehető leggazdaságosabbnak kell lenniük, amely folyamatirányítási és közgazdasági feladat megoldását is szükségessé teszi. Az egyes végtermékek, félkész-termékek minőségét és árát alapvetően a fenti tényezők, az egyes feladatok megoldásának sikeressége határozza meg. A mérnöknek tehát, amennyiben sikeres technológiai tervet kíván készíteni, az előzőkben vázolt tudományterületeken, azaz az anyagtudományban, a kontinuum-mechanikában, az egyes technológiai eljárásokban, valamint a gazdaságtudományban egyaránt megfelelő ismeretekkel kell rendelkeznie. Figyelembe véve a tervezés során számításba veendő paraméterek nagy számát – anyagjellemzők, gyártási folyamatot leíró paraméterek, stb. -, a közelmúltig az ún. “trial-and-error” – “próbáld és korrigáld” – eljárás dominált a technológiák fejlesztése terén. Ezen módszer egyik legjelentősebb hátránya az igen nagy idő- és kísérleti munka igénye és ennek egyenes következményeként a módszer igen költséges volta. Ezen felül a módszer eredménye nagymértékben függ a tervezőmérnök, illetőleg a technológus tudásától, felkészültségétől, képességétől. Ezért folyamatosan fejlődtek az egyes feladatok megoldását segítő analitikus és numerikus módszerek is. A figyelembeveendő paraméterek nagy száma miatt azonban, a technológiai folyamatok többségére nem lehetett ilyen jellegű megoldásokat találni. Az elmúlt 10-15 évben a számítógépek és a kapcsolódó szakterületek gyors fejlődése, a numerikus eljárások általánosabb alkalmazását, a gyártástechnológiai folyamatok tervezésére való adaptálhatóságát eredményezték. E módszerek közül az egyik leghatékonyabb a véges elemes módszer. A napjainkban elérhető jelentős számítástechnikai kapacitásnak köszönhetően e numerikus eljárások alkalmazása viszonylag rövid futási idő mellett közel valós-idejű (real-time) megoldásként lehetséges, azaz e rendszerek az akadémiai kutatások keretei közül kinőve, valós ipari körülmények között is alkalmazhatóvá váltak. E módszereket ma már az iparban elterjedten alkalmazzák a technológiai folyamattervezésben és a szerszámtervezés terén egyaránt. Az ipari alkalmazhatóság természetesen nem csak a számítási teljesítmény függvénye. Egyre erőteljesebb az igény speciális feladatok gyors megoldását lehetővé tevő rendszerek iránt. Ez indította el a célfeladatok megoldására alkalmas, ún . "feladat-orientált" programcsomagok kidolgozását. Ezek általában csak egyes technológiák, vagy szűkebb technológiai csoportok elemzésére alkalmasak. Legnagyobb erősségük, hogy a feladat jól definiálhatóságából következően igen pontosan meghatározható technológiai paraméterekre épülnek. Ez lehetővé teszi az elemzés folyamatának automatizálását. A rendszerek kezelői felületei jól áttekinthetők, gyakorta alkalmazhatók számottevő numerikus alapismeretek nélkül, jelentősen segítve a szerszám és technológiatervezésben jártas – nem feltétlenül mérnöki végzettségű – technológus munkáját is. Ilyen jellegű program például a lemezalakító folyamatok technológiai tervezésében alkalmazható, az autóiparban elterjedt AutoFormÔ , vagy a térfogat-alakításban használható QFormÔ .Ezen rendszerekre, elsősorban a kezelői felületeikre is jellemző a numerikus megoldási mó dszerek egy másik fejlődési iránya, amely elsősorban integrált programcsomagok kidolgozását célozza. Ezek lehetővé teszik egy-egy feladat automatizált, felhasználói beavatkozást csak minimális mértékben igénylő megoldását. E cél érdekében általában numerikus, (például VEM) kódokat ötvöznek tudásalapú rendszerekkel. Jellemző példa erre a rendszercsoportra a jelenleg béta tesztelés alatt álló AutoFormÔ Die Designer modulja, amely lehetővé teszi a húzott alkatrész geometriájából a húzáshoz szükséges bélyeg és matrica közelítő alakjának előállítását is.Az elmúlt 10-15 évben a Miskolci Egyetem Mechanikai Technológiai Tanszékén számos, a fent vázolt két fejlődési irányhoz kapcsolódó kutatási program folyt. A következőkben a Tanszék ilyen irányú tevékenységéről adunk rövid összefoglalást.
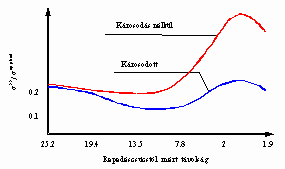
2. Alapkutatási feladatok A Tanszéken futó kutatási programok részben olyan kérdésekre is választ kívánnak adni, amelyek jelentősen túlmutatnak az egyes ipari megbízások keretein. A tanszék számos olyan, hazai és nemzetközi együttműködésben is részt vesz, amelyekben a munka célja általánosan használható, több ipari probléma esetében is alkalmazható megoldás kidolgozása. Ebben a pon tban az ebbe a csoportba sorolható kutatásokról adunk rövid összefoglalót. Terjedelmi okokból e helyen természetesen csak egy-egy szemelvény bemutatására vállalkozhatunk.2.1Bemetszett próbatestek szívós törése [1] Első példaként egy, a NATO " Science for Peace" (Tudomány a Békéért) programja által támogatott, magyar, cseh és francia intézetekkel közösen végzett kutatás numerikus modellezéshez kötődő részét ismertetjük. A program célja az atomreaktorok elhasznált fűtőelemeinek biztonságos tárolását, illetve szállítását lehetővé tevő tartályok anyagának vizsgálata, illetve új tartályanyagok alkalmazhatóságának elemzése. Mivel a tartályanyagok integritását szélsőséges körülmények között is meg kell őrizni, a legkülönfélébb törési folyamatok vizsgálata, illetve numerikus elemzése a projekt fontos részét képezi. A következőkben röviden a szívós töréshez kapcsolódó eredményekkel foglalkozunk.A szívós törés egyik jellemző problémája a képlékeny alakváltozási mechanizmus változása. Az addig homogén anyagban hibák, mikroüregek, mikrorepedések jelennek meg. Ezek a további képlékeny alakítás hatására növekednek, alakjukat változtatják. A keletkezett hiba terjedőképessé válva makrorepedésként viselkedhet és a szerkezet törését okozhatja. A törés e lkerüléséhez, illetve a szerkezeti elem időben történő cseréjéhez a megfelelő károsodási mechanizmusok ismerete szükséges.E kutatási program fő célkitűzése a szakirodalomban található, károsodásmechanikai mode llek elemzése, numerikus integrálása. Ezek alkalmazásával megmagyarázhatóvá, ezáltal előre jelezhetővé válik a reaktoranyagok viselkedése, töréssel szemben tanúsított ellenállása. A következőkben bemutatandó példa egy, a szakirodalomban csak az elmúlt évben megjelent, károsodott anyagokat leíró képlékenységi feltétel numerikus integrálása, illetőleg az elkészült numerikus kód alkalmazása bemetszett próbatest repedéscsúcsban kialakuló feszültségeloszlásának számítására. Az általunk alkalmazott képlékenységi feltétel legnagyobb előnye az egyéb hasonló összefüggésekhez képest a rendkívül egyszerű, automatizálható paraméter meghatározásban rejlik.A numerikus integrálás után egyszerűen számítható a károsodás hatása a feszültségi és ala kváltozási mezőre – ezt szemlélteti az 1.a. ábra –, illetve összehasonlíthatóvá válik a károsodott és nem károsodott anyagok esetében a repedéscsúcsban kialakuló, jellemző feszültségkoncentráció, amely az 1.b. ábrán látható.
A projekt jelenleg futó részének célja a numerikus analízis eredményeire és a lejátszódó fizikai folyamatokra épülő törési feltétel kidolgozása. 2.2 Ellenállás ponthegesztés hőfolyamatainak elemzése [2] Az ellenállás-ponthegesztést 1877-ben Elihu Thomson fejlesztette ki és alkalmazása gyorsan terjedt a vékonylemezes konstrukcióknál. Annak ellenére, hogy a technológia több mint 100 éves, az eljárás fizikai jelenségeit még a mai napig sem sikerült maradéktalanul feltárni. Ennek oka elsősorban az, hogy az ellenállás-ponthegesztés elektromos, termikus, mechanikai és metallurgiai jelenségek összetett folyamata, ráadásul e hatások nem önmagukban, hanem csatoltan, azaz kölcsönösen egymásra hatva jelentkeznek.
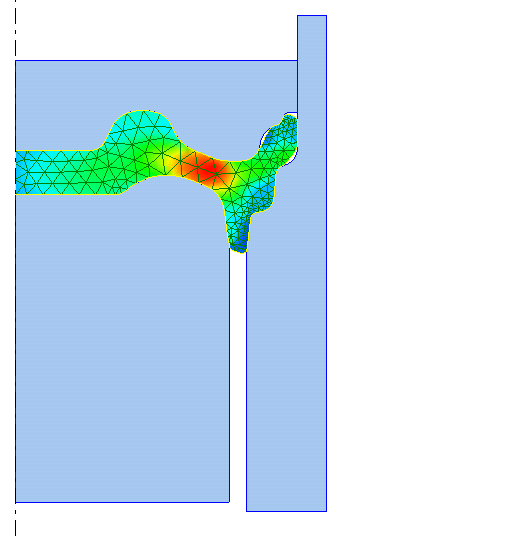
Jelen kutatási program fő célja az ellenállás-ponthegesztés korai, (az összefüggő érintkezési felület kialakulásának pillanatáig tartó) szakaszának végeselemes modellezése. Ennek érdekében az ellenállás-ponthegesztés modellezésére egy mechanikai és egy hőtani modellt építettünk fel, majd a hegesztett kötés létrejöttének folyamatát ezek összekapcsolásával vizsgáltuk. A modell a 2.a. ábrán látható. Fémtiszta felületeket feltételezve elsősorban azt elemeztük, milyen hatással lehetnek a mechanikai- és hőterhelések a felületi érdességre és az oxid-rétegre. Ennek érdekében meghatároztuk adott terhelések mellett a redukált feszültségek és alakváltozások változását. Ez a munka része annak a tanszéki kutatási témának, amely a hegesztési hőfolyamatok analitikus végeselemes és az ún.véges térfogatos (FVM) analízisére épül. E kutatás egy jelenleg futó Ph.D. program témája is.A redukált feszültségértékek nagysága – 2.b. ábra – az ellenállás-ponthegesztett kötés kialakulása szempontjából azért döntő, mert az érintkezési felületen azok az érdességi csúcsok deformálódhatnak legjobban, amelyeken a redukált feszültség értéke nagyobb. Hangsúlyozni kell, hogy a kristályos szerkezetű anyag felületén melegítés hatására a kiemelkedések egy része kisimul, de egyidejűleg újabb egyenetlenségek is keletkezhetnek, így e folyamatra döntő hatással van a redukált feszültségérték. A modellalkotásnál az elektromos jelenségeket ugyan nem vettük figyelembe, de fontos megemlíteni, hogy az érintkezési csúcsok felületének nagysága fontos szerepet játszik az átáramló áramsűrűség szempontjából. A kutatás fontos célkitűzése az alkalmazott anyagmodellek pontosítása.
3. Alkalmazott kutatások Az alapkutatások mellett az ipari gyakorlatban közvetlenül felhasználható eredményekre vezető alkalmazott kutatások a tanszéken kiemelt jelentőségűek. E kutatások nagy része hazai, illetve nemzetközi ipari és akadémiai partnerekkel folyó együttműködésekhez is kapcsolódik. A következőkben e területről mutatunk be szemelvényeket, elsősorban olyan kutatási témákból, amelyek interdiszciplináris megközelítést igényelnek. 3.1 Fém-kerámia határfelület mechanikai jellemzői [3] Az autóipar, de a gépipar számos más területe számára is igen jelentős a késztermék teljesítményének folyamatos növelése, a beépített anyagok tömegének és árának csökkentése mellett. A teljesítmény növelésének egyik módja a nagy kopásállósággal rendelkező kerámiák alkalmazása. Tekintettel ezen anyagok rideg viselkedésére, illetve rendszerint magas árára, folyamatos tervezési törekvés kiváltásuk olyan helyeken, ahol nem feltétlenül szükséges alkalmazásuk, illetve olcsóbb fémekkel kombinált beépítésük egyenértékű megoldást jelent. Fontos ipari feladat ezért a fém és kerámia darabok kötéseinek vizsgálata, a kialakult kötés minőségének elemzése. E kutatási program célja olyan VEM modellezésre épülő módszer kidolgozása, amely lehetővé teszi a kötés tulajdonságainak előrejelzését a gyártási technológia ismeretében. A fém és kerámia alkatrészek összeillesztése során egy határfelület alakul ki a két anyag között. Ez a határréteg, amely a kész darab tulajdonságait jelentősen befolyásolja harmadik anyagként is kezelhető. E réteg mechanikai tulajdonságai meghatározhatók. E harmadik anyag segítségével az egyesített kerámia-fém alkatrész mechanikai és termikus tulajdonságai az eddigieknél pontosabban számolhatók, illetve a technológiai tervezés során előre jelezhetők. További feladat a határfelület ideális alakjának számítása. Ehhez számos kritérium fogalmazható meg. Ilyen lehet például a gyártás során visszamaradó feszültség minimalizálása, vagy az üzemi hőmérséklet növelésének kritériuma. Az utóbbi feltétel, vagyis a maximális üzemi hőmérséklet megválasztásához számos VEM szimuláció f uttatásával juthatunk el. A 3.a. ábra szinuszos határfelület esetére mutatja a hevítés közben kialakuló feszültségeloszlást. A 3.b. ábra lehetővé teszi a hevítés hatásának vizsgálatát egyes határfelület-geometriák esetén, illetve a legelőnyösebb geometria kiválasztását. Az eddigi elemzések alapján a vizsgált esetek közül a legkedvezőbb a feszültségeloszlás a konvex felület alkalmazásával.
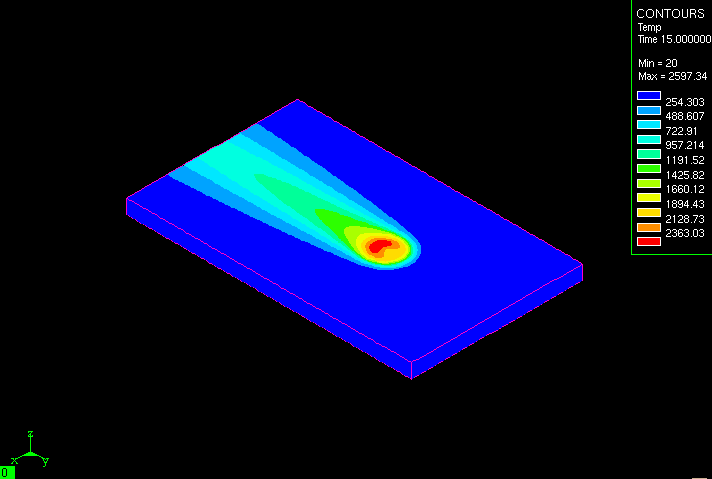
3.2 Forgóíves hegesztés elemzése [4] A hegesztés termelékenységének növeléséhez a hegesztés hőforrásának teljesítményét kell növelni. A nagyobb termelékenységű, esetenként új hegesztő eljárások alkalmazásának határa is csak a hegesztési hőfolyamat elemzése alapján, a hegesztési hőfolyamatban végbemenő változ ások pontos ismeretében jelölhető ki. Bár a hagyományos hegesztő eljárásoknál már régóta ismertek az ív által keltett hőáramsűrűség mező leírása alkalmas összefüggések, de a forgóív hőáramsűrűség mezejének matematikai modellezésére, analitikus leírására - annak ellenére, hogy maga a jelenség már közel 40 éve ismert - eddig még nem született eredmény. A probléma szerteágazó és bonyolult volta miatt a fenti témával foglalkozó – és csak a hagyományos hegesztési eljárásokat vizsgáló – meglehetősen nagy számú tanulmány jellemzője, hogy csak közelítő számításokat tartalmaz. A különböző egyszerűsítések, elhanyagolások esetenként egymásnak ellentmondó eredményekhez vezettek, ugyanakkor a méréseknek, valamint a mérési eredmények kiértékelésének is vannak bizonyos nehézségei.A problémakör vizsgálata, a forgóív hőáramsűrűség mezejé nek leírására alkalmas összefüggések kidolgozása - annál is inkább fontos és szükséges - mivel a forgóíves hegesztési folyamatot jellemző nagy sebesség és hőmérséklet, illetve a problémakör bonyolultsága miatt, bizonyos vizsgálatok az esetek nagy részében már csak – az ipari gyakorlatban is egyre nagyobb tért nyerő – különböző végeselemes módszerekkel lehetséges.Forgóíves hegesztéskor az ív részét képező és a munkadarabon létrejövő aktív folt (jelen ese tben a katódfolt ) a huzalelektróda szimmetria tengelyéből kitérve egy (az ívfeszültségtől függő) R sugarú körpályán mozog. Ekkor a hőáramsűrűség mezőt egy, az ívtalpponttal együttmozgó Gauss-féle harangfelület reprezentálja. Ugyanakkor – egyszerűsítésként - az adott pontban, adott időpillanatban a hőáramsűrűség eloszlást reprezentáló Gauss-görbét önmagára nézve tengelyszimmetrikusra vesszük fel és eltekintünk attól, hogy a görbe külső részén, illetve a forgástengely felöli belső részén az egyenlőtlen hevítési és hűlési viszonyok miatt a hőmérséklet eloszlást leíró görbeszakaszok egymástól kissé eltérő alakúak. A levezetéseket mellőzve a hőáramsűrűség függvény az alábbi formában írható fel:
amelynek segítségével meghatározhatjuk a forgóív által keltett hőáramsűrűség mezőt az egész felületre.Ha az ív kellően nagy szögsebességgel forog körbe (egy körülfordulás alatt a hűlés mértéke elhanyagolható), akkor a körbe forgó harang felület által létrehozott hőáramsűrűség mező h elyettesíthető egy olyan burkoló felülettel, amely alatti hőáram (F ) azonos a forgó ív által - egy körbefordulás alatta – a felületbe juttatott hőárammal. A forgóívre jellemző hőáramsűrűség eloszlás burkolófelületének közelítő meghatározásánál figyelembe vesszük, hogy a valóságban az ív nagy fordulatszámmal forog (500- 700 1/s), ezért helyénvaló az a feltételezés, hogy a haranggörbének az R sugarú körön való körülhaladása által meghatározott térbeli alakzat burkoló felületével arányos felülettel helyettesítjük a forgóív hőáramsűrűséget.
A helyettesítő burkoló felület - a függőleges síkmetszetén vett - meridián görbéjének a jobb és baloldali R, -R helyeken lévő Gauss-görbe A modell segítségével és a Sysweld+ programmal végzett – a varrat környezetében kialakuló hőmérséklet meghatározására irányuló - futtatások néhány eredményét a 4.b. ábra mutatja. A VEM analízisek és a vele párhuzamosan végzett gyakorlati kísérletek alapján bebizonyosodott, hogy az eddig a varrat környezetében létrejövő hőmérséklet eloszlás leírására szokványosan alkalmazott Rykalin-Okerblom összefüggés nem alkalmas a forgóív környezetében kialakuló hőmérsékleti állapot leírására, hanem annak módosítása szükséges.
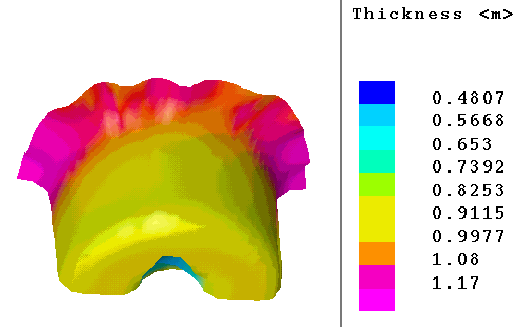
4. Többlépcsős alakítások elemzése Egy további alkalmazási terület, amelynek rövid elemzésére kitérünk, a többlépcsős képl ékenyalakítási technológiák tervezése tulajdonképpen túlmutat az eddigieken, részben a következő főpontban tárgyalandó témakörhöz is sorolható. Az ilyen, összetett technológiák tervezése ugyanis meglehetősen bonyolult, elsősorban a közbenső-, illetőleg a kiinduló geometriák meghatározása miatt. A hagyományos tervezési eljárások esetében e közbülső geometriák tervezése gyakorlati szabályokon és nagyrészt a tervező tapasztalatán és intuícióin alapul. A valamilyen jósági kritériumon alapuló automatizált geometria-tervezés tudásalapú, illetve inverz numerikus megoldást igényel. Itt két alkalmazási példát mutatunk be, amelyek esetében a numerikus elemzés elsődleges célja a már kidolgozott geometriák gyárthatóságának elemzése. Az 5.a. ábrán autó oldalpanel többlépéses alakítása, míg az 5.b. ábrán fogaskerék meleg térfogatalakításának egy közbenső lépése látható. Mindkét esetben alakváltozásokat jelenítettünk meg: egyrészt a lemezvastagság változását, illetve az alakváltozási mezőt.
5. Numerikus alkalmazások komplex rendszerekben [5], [6] Az előzőkben olyan kutatási feladatok megoldásával foglalkoztunk, amely ek során jól körülírható bemenő adatok – anyagparaméterek, geometria, súrlódási adatok – ismeretében az elemzés célja az egyes technológiák megvalósíthatóságának vizsgálata, illetve a technológiákat befolyásoló paraméterek hatásának elemzése. Ez utóbbinál teljes tartományban változtathatók az egyes paraméterek értékei, és a kísérleti megoldásoknál jóval gyorsabban előállíthatók a kívánt eredmények.
A gyakorlati életben azonban számos olyan feladat van, amikor a technológiai paraméterek egy része nem körülhatárolható értékeket vehet fel. Ilyen eset például a már említett többlépcsős alakítás, ahol nemcsak a kiinduló előgyártmány alakja, a közbenső geometriák sem ismertek. Hasonlóan, legtöbbször a súrlódási adatok, az anyagparaméterek értékei sem pontosan adottak. A szimuláció eredménye pedig igen erősen függ ezeknek a paramétereknek az értékétől. A következőkben azt mutatjuk meg, hogyan lehet magát a Véges Elemes Rendszert arra felhasználni, hogy a VEM szimulációhoz bemenő adatokat nyerjünk. Tételezzük fel, hogy olyan folyamatot kívánunk szimulálni, amelyet kísérletileg is el tudunk végezni. Ebben az esetben ismertek azok a kísérleti adatok, lemezvastagság változása, nyúlások, hőmérsékletváltozás, stb., amelyeket a VEM analízis eredményeként megkaphatunk. Természetesen, nem pontosan ismert, tehát nem pontosan megadott bemenő adatok esetében a szimuláció eredménye nem egyezhet meg a kísérletileg mért értékekkel. Ekkor módosítanunk kell a bemenő adatokat, majd újra futtatni az elemzést. Az új eredmények – a kísérleti és mért értékek eltérése – alapján, amennyiben szükséges, a bemenő paraméterek értéke tovább módosítható. Ez a folyamat addig folytatható, amíg a mért és a számított értékek egy előírt hibahatáron belül megegyeznek. Ezzel a módszerrel a paraméterek meghatározása tulajdonképpen egy optimálási feladatra vezethető vissza. Az így felépülő rendszer, amelynek működési elve a 6.a. ábrán látható, az Inverz VEM program. A 6.b. ábra a lemezanyagok anyagparamétereinek meghatározására alkalmas tesztgeometriát mutatja. Értelemszerűen, többlépcsős alakítások esetében az egyes lépésekben legmegfelelőbb geometria számítása is hasonló feladatként oldható meg.
6. Összefoglalás E cikkben a Miskolci Egyetem Mechanikai Technológiai Tanszékén az anyagtudomány és az anyagtechnológiák területén folyó modellezési és szimulációs kutatásokból mutattunk be néhány alap-, illetve alkalmazott kutatást. A konkrét kutatási témákon keresztül röviden bemutattuk a VEM főbb technológiai alkalmazási területeit, alapkutatási, ipari gyakorlati alkalmazhatóságát, illetőleg egy VEM alapú komplex rendszer felépítését. Összefoglalóan megállapítható, hogy napjainkra a VEM módszer mind a tudományos kutatásban, mind az ipari-gyakorlati kutatásokban, mindpedig az oktatásban jól hasznosítható, egyre szélesebbkörű alkalmazást nyert.
7. Irodalom [1] Pluvinage G., Fülöp T., Tisza M., Notch effect and damage processes, Brno, 2000. május 28-29. [2] Szabó P., Balogh A., Az ellenállásponthegesztett kötés kezdeti szakaszának végeselemes modellezése, Gépészet 2000, Budapest, 2000, május 24-25 [3] Tisza M., Nagasawa S., Fukuzawa Y., Rowshan R., Fülöp T., Mechanical analysis of metal-ceramics interlayers, Gépészet 2000, Budapest, 2000, május 24-25. [4] Adorján G., Forgóíves hegesztés modellezése, MicroCAD’2000, Miskolc, 2000. február 23-24. [5] Kuzman K., Gantar G., Tisza M., Magyar Z., Fülöp T., Development of test geomety for inverse FEM, Gépészet 2000, Budapest, 2000, május 24-25 [6] Tisza M., Integration of numerical modelling and knowledge based systems in metal forming, ICTP’99, Nürnberg, Springer, 1999. v.1. p. 117-128.
|
|||||||||||||||||||||||||||||||||