
Mind a párologtatásnál mind a porlasztásnál szükséges a kiépülő réteg vastagságának a technológiai folyamat alatti kontrollja, mert csak ezzel biztosítható az eljárás végpontjának jelzése. Értelemszerű, hogy — gyakorlatilag minden esetben — egy adott rétegvastagság előállítása a cél, és ez a vastagságérték a kívánttól nem térhet el számottevően. (A megengedett eltérés a felhasználástól függ, de általában 1 - 10 %.)
Igen kritikus pl. az alumínium réteg vastagsága a felületi hullámú akusztikus szűrőknél, míg az IC fémezésnél a megkívánt pontosság az előírt érték ± 5 % -a.
Optikai rétegeknél az un. T bevonatoknál egy hullámhosszra vonatkoztatva a rétegvastagság pontosan l /4 kell legyen, és e feltételnek az optikai elem egész felületére teljesülnie kell.
Ezek az igények hívták életre az "in situ" rétegvastagság méréseket, mert az utólagos mérés csak informatív jellegű, és a kialakított réteget számottevően már módosítani nem lehet. Ezért tehát a folyamat alatti mérés elengedhetetlen feltételévé vált a PVD technikáknak.
6.1.1. Rezgőkvarcos rétegvastagság mérés. (In situ)
A rezgőkvarcos vastagságmérés azon az elven működik, hogy egy kondenzátorrá kialakított SiO2 egykristály lemez rezgésbe hozható, ha villamos váltófeszültséggel tápláljuk ezt a kondenzátort. (Elektrostrikció jelensége.) Kellő feltételek mellett az így kialakított rendszer sajátfrekvenciáján rezgésbe hozható, és ez a rezgési frekvencia igen széles hőmérséklet határok között viszonylag nagy pontossággal (Df/f = 10-6 ) stabil. E jelenséget alkalmazzák a kvarc órák vezérlésénél is.
A rendszert, mely a kvarcot és annak gerjesztését végzi, együttesen kvarc oszcillátornak nevezik. (A kvarc a piezoelektromos sajátosságát az ultrahang keltő berendezések un. transzducerében is felhasználják. Ma már e két utóbbi alkalmazás a vázolt jelenség legszélesebb alkalmazási területe.)
A rétegvastagság mérésre a kvarcot az teszi alkalmassá, hogy a sajátfrekvenciát a — méretei mellett — a tömege is meghatározza. Ezért, ha a rétegleválasztás folyamata során a réteg a kvarcon is épül, a annak tömegét, és ezzel a frekvenciáját is megváltoztatja (csökkenti). Ismerve a kvarcon kondenzálódó anyag felületét, és sűrűségét, a frekvencia változásból a tömeget, a rétegvastagság meghatározható.
Gondot okoz, hogy a leválasztott réteg sűrűsége a legtöbb esetben nem egyezik meg a tömör anyag (bulk) sűrűségével, ezt a tényt korrekcióval figyelembe kell venni.
A 6.1. ábrán látható egy mérőkvarc kialakítása, és a mérőrendszer sémája.

Az elektródák anyaga általában párologtatott ezüst (egy konkrét esetben [MIKI rétegvastagság mérő] 200 nm), de lehet más a anyag is.
A mérőkvarc tömegváltozása korlátozott, és a konkrét rendszerre adott, azt meghaladva a rendszer nem lineáris, és egy határon túl a rezgés leáll. E tartomány az említett esetben (az alapfrekvencia 5 MHz) 100 kHz. Ha a kristály ennél (4,9 MHz) kisseb frekvencia tartományba kerül, akkor fel kell újítani. Ez a kondenzált réteg eltávolítását jelenti, ami például kémiai marással történhet. Ez indokolja az ezüst elektródákat. Ha az elektródák más anyagból készülnek, akkor a marás azokat is eltávolítja, és külön vákuumciklusokban azokat újra fel kell vinni. Ehhez párologtató sablont mellékelnek a műszerhez.
A rezgőkvarcos mérés az "in situ" mérések között a legpontosabb, de számos korlátja van. Ezek közül az egyik az, hogy míg a hordózókat általában a bolygó karusszelen helyezik el, addig a kvarc mérőfejét — a nagyfrekvenciás villamos csatlakozás miatt — oda építeni nagyon nehéz, ezért álló kvarccal dolgoznak, melyet hitelesíteni kell ez esetben minden technológiára.
További korlátot jelent, hogy a kvarc 120 oC felett károsodik (ikresedés), és rezgési tulajdonságai megváltoznak. A mérés igy nem lesz hiteles. Ha a mérőfej a rétegleválasztás során hőhatásnak van kitéve a fejet vízzel hűteni kell. (A fej kialakítása olyan, hogy hűtő cső helyezhető rá.)
Pontatlanságot okoz a már említett különbség a bulk és a vékonyréteg eltérő sűrűsége is. A vázolt okok miatt az "in situ" mérést célszerű hitelesíteni egyéb vastagságmérésekkel.
A mérés pontosság fokozható, ha nem a frekvencia - változást, hanem a periódus idő változását méri az elektronika.
A kijelezés lehet digitális, vagy analóg. A digitális kijelzés előnye, hogy nemcsak a rétegvastagság, hanem a frekvencia is kijelezhető, jobb esetben 1 Hz pontossággal.
További igényt is kielégített ez a mérés, nevezetesen a folyamat vezérlést, automatizálást, több réteg felvitele esetén is. Szabályozhatóvá tette a réteg épülési sebességet, és számítógéppel kombinálva automatizálhatóvá vált a teljes gyártási ciklus. (A vákuumrendszer leszívását és lelevegőzését is beleértve.)
Ezen lehetősége, és a pontossága miatt ez a legelterjedtebb "in situ" mérés.
6.1.2. Interferenciás mérés. (In situ)
Optikai rétegek PVD eljárással készített változatainál használatos "in situ" mérésmódszer. Elvi alapja az az ismert jelenség, hogy adott hullámhosszúságú fény a l /4 vastagságú rétegen áthaladva (a beeső és a visszavert réteg interferenciája miatt) kioltást szenved. A kioltás mértéke a reflexió nagyságától függ, de a legritkább esetben teljes.
A 6.2. ábrán látható a mérőrendszer felépítése és elhelyezése a vákuumrendszeren.
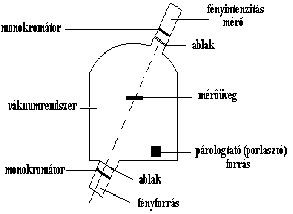
6.2. ábra
A fényforrásból kibocsátott fény a monokromátoron, a mérőüvegen, a második monokromátoron keresztül az intenzitásmérőbe kerül.
A rétegvastagság mérés természetesen pontatlan. A legalsó méréshatár l /4, és viszonylag pontosan csak ennek egészszámú többszörösét lehet mérni. A mérőlemez és a párologtató forrás elhelyezése miatt a mérőlemez felületén kondenzálódó réteg vastagsága nem egyenletes, ezért a kioltás sem minden pontban teljesül, ez is bizonytalanná teszi a mérést.
A fényforrást és az indikátort tartalmazó tubusokat a a vákuumrendszeren gyárilag kialakított karimákra lehet erősíteni, valamint a tubusokat minden irányban elmozdíthatóra képezik ki az optikai egytengelyűség beállíthatósága érdekében. Az ábrán feltüntetett ferde elhelyezésen kívül van olyan vákuumrendszer is a mi a merőleges szerelést teszi lehetővé.
6.1.3. Ellenállás mérés. (In situ)
Jellemzően ellenállás rétegek (pl.: NiCr) gyártásánál használják. Előnye, hogy rendkívül egyszerű, és az adott feladatra pontos is.
A mérés elve, hogy szigetelő hordozón kialakuló réteg ellenállását mérik a rétég épülés alatt. Ha a mérőlemezt úgy alakítják ki, hogy a = b (6.3. ábra) akkor az mért ellenállás közvetlenül a réteg négyzetes ellenállás értékét szolgáltatja.
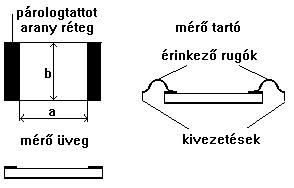
6.3. ábra
A mérést természetesen legpontosabban Wheatstone hídban célszerű végrehajtani.
E mérés is alkalmas a végpontnál a folyamat leállítására, de nem megfelelő a folyamat vezérlésére, mert a rétegellenállás -- a folyamat megindulásakor -- nem lineárisan függ a rétegvastagságtól.
A legelterjedtebb felhasználása a NiCr ellenállás rétegek gyártásánál van, de itt is figyelembe kell venni, hogy a hordozók a bolygókarusszelen vannak, míg a mérőellenállás általában áll. További korrekciós tényezőt jelent az, hogy az ellenállás réteg hőkezelés nyomán nyeri el a végső értékét, igy a vákuumfolyamat során lényegesen eltérő négyzetes ellenállás értékű réteget kell előállítani, mint amilyenre a felhasználás során szükség van. Ez további korrekciót igényel. Ezek miatt gyakorlatilag itt is kísérletileg kell beállítani a kívánt rétegvastagsághoz a tartozó mérendő ellenállás értéket.
6.1.4. Rétegvastagság mérése tapintótűs méréssel
Rétegvastagság mérése számos elvi és gyakorlati kérdést vet fel. Gyakorlati oldalról nézve a probléma az, igen sokféle eljárás létezik, melyek a legkülönbözőbb fizikai jelenségen alapulnak és ezek a jelenségek egymással vagy egyáltalán nincsenek kapcsolatban vagy a kapcsolat eléggé laza. Tehát különböző módon mért vastagságok nem bizonyos, hogy azonosak. Ez azt jelenti, hogy vastagságfüggő tulajdonságok megadása nem mindig egyértelmű. [6.1.]
Másik gyakorlati kérdés, hogy az eljárások egy része roncsolásos, vagyis a réteg már nem használható eredeti céljának megfelelően.
Nyilvánvaló, hogy más módszer kell az in situ (előállítás közbeni) méréshez, ahol figyelembe kell venni az előállítás módját (pl. nagyenergiájú plazmás eljárás, maró reaktív gázok) és más a kész réteg utólagos vizsgálatánál. Mást kell a laboratóriumi, kutatást célzó vizsgálatokhoz és más a termelés rutinjellegű méréseihez.
A mérések elve nagyrészt régóta ismert, de egyesek gyakorlati alkalmazása csak 1-2 évtizede jött el, mások pedig az idők folyamán érdektelenek lettek.
Elvi kérdések megválaszolása komolyabb nehézségeket jelenthet. Ha ugyanis rétegvastagságról beszélünk, hallgatólagosan fel szokás tételezni, hogy a réteg két párhuzamos felülettel vagy síkkal határolt. A vastagság pedig az adott felületek normálisa metszéspontjainak távolsága. Ez a valóságban a legritkábban valósítható meg. A valóságban ugyanis mind a hordozó-, mind a réteg felső határfelülete bizonyos egyenetlenséggel rendelkezik. Igen vékony rétegek sokszor különálló szemcsékből állnak, itt réteg felületéről beszélni értelmetlenség.
A valós rétegek esetében tehát valamilyen átlagos értéket mérünk, mely átlag erős függvénye a mérési elvnek és módszernek. Az össze nem függő réteg vastagságát még a szemcsék alakja is befolyásolja, így tulajdonképpen a morfológiai vizsgálatból kellene átlagot számolni. Ezért azok a szerzők, akik az adatok egzakt megadására törekedtek, mindig megadták, hogy a vastagságot milyen módszerrel határozták meg. Így alakultak ki olyan fogalmak, mint "tömegvastagság" (épisseur massique) "geometriai vastagság" stb.
A tapintótűs mérés talán a legkézenfekvőbb vastagságmérés. Ugyanis az emberi érzékelések legáltalánosabbjához áll legközelebb. A műszer lelke egy gyémántcsúcs, melynek görbületi sugara néhány mm. A csúcs igen könnyű, elektromágnesesen kiegyensúlyozott karon helyezkedik el, a kar általában torziós szálon függ. A tű kis nyomással nehezedik a rétegre, melynek felületét valamely irányban mozogva végigtapogatja. Ha a hordozón a réteg úgy jött létre, hogy éles határvonalú lépcső van a fedett és nem fedett rész közt, a lépcső magasságát a tű követi és a mozgását a kar közvetítésével elektronikus úton felerősítve egy regisztrálóba vezetik. A tű görbületi sugarától függően többé-kevésbé követi a felület egyenetlenségeit is, sőt a különálló szemcsék jelenlétére is utalhat. A műszer erősítésének függvényében a mérhető rétegvastagság néhány nm-től általában 10-50 m m-ig terjed. Az erősítés a könnyű értékelés érdekében dekádikus osztással szabályozható. A mérés pontosságát károsan befolyásolhatja a hordozó (és vele a réteg) rövid periódusú hullámossága. A mérőeszközt a különböző gyártók Talystep, Alphastep, Talysurf, Profyler stb. név alatt hozzák forgalomba, lényegében azonos működési móddal, és legújabban számítógépes kiértékeléssel kombinálva.
6.1.5. Interferometriás mérés.
Ezzel a módszerrel az "optikai" vastagságú rétegek vastagsága mérhető igen pontosan. Az "optikai" jelző azt jelenti, hogy a réteg vastagság a megvilágító fény hullámhosszának nagyságrendjébe esik, azaz a felületre merőlegesen beeső fényhullám interferenciaképes. A szóba jöhető vastagság kb. 1/20 l < d < 5l tartományban változhat.
Két különböző módszer ismeretes az interferometrikus vastagságmérésre. Az egyik az interferencia révén kioltódó fény hullámhosszának mérésén alapszik, a másik pedig ék formájú síkok közt létrejövő interferenciacsíkok eltolódását méri.
a.) Az első módszer kizárólag átlátszó réteg esetében alkalmazható, a hordozó elvileg fém is lehet. A lényege a módszernek, hogy a réteg két határfelületéről reflektálódó fénysugarak kioltják egymást, ha a réteg optikai vastagsága nd = (2k+1)l/4 , ahol n a törésmutató, k egész szám 0, 1, 2, 3 stb. Ismeretlen az nd és k. Ezért a réteget fehér fénnyel világítják meg és a reflektált fényt monokromátorba vezetik. Itt a spektrumban megjelennek a kioltásnak megfelelő sötét vonalak. Két szomszédos vonal l1 és l2 hullámhosszát megmérve, két egyenletet kapunk, melyből k és nd meghatározható. Az eljárást Schöder fejlesztette ki. Vasicek [6.2.] egy adott hullámhosszú fénnyel világítja meg a réteget, de két különböző beesési szögben, így nyeri a két egyenletet.
Az eljárás nagy előnye, hogy roncsolásmentes, hátránya, hogy csak viszonylag vastag rétegek esetén pontos, továbbá ismerni kell a réteg törésmutatóját. Amennyiben a réteg anyaga ismert, ez utóbbi nem jelent komoly hátrányt, mivel a viszonylag vastag réteg törésmutatója nem tér el lényegesen a tömbanyagétól.
A módszerhez hasonló elven egy szubjektív eljárás is van: a reflektált fényben a kioltott hullámhosszú fény komplementer színei jelennek meg. Színskála alapján kis gyakorlattal meglepő pontossággal becsülhető a réteg optikai vastagsága.
b.) Interferenciacsíkok módszere. A módszer végső kidolgozása Tolansky nevéhez fűződik [6.3.] soksugaras interferencia néven. Alapgondolata: ha egy Fabry-Perot interferometerben a féligáteresztő tükröket ék alakban helyezi el, a változó útkülönbségeknek megfelelően egyenlő osztással sötét interferenciacsíkok jelennek meg a kioltási helyeken. A csíkok távolsága l /2 útkülönbségnek felel meg.
Vastagságméréshez a F-P szűrő egyik lemezére visszük fel a réteget, illetve a hordozón lévő réteg egy részét eltávolítjuk. A másik fémet tartalmazó lemezt állítócsavarokkal addig állítjuk, míg a csíkok megjelennek. Ha a réteg széle meredek, a határfelületnél a csíkok eltolódnak egy Da értékkel. Ha a csíkok távolsága a, Da/a viszony megegyezik 2d/l értékkel. A csíkok jó kontrasztossága érdekében a réteg és hordozó üres felületét tükröző fémmel be kell párologtatni vagy porlasztani, továbbá monokromatikus fénnyel kell megvilágítani. Miután a réteget részlegesen el kell távolítani a hordozóról és az egészet fémezni kell, a mérés roncsolásosnak tekinthető és hosszabb előkészületet igényel. A berendezés tulajdonképpen igen egyszerű. A F-P féligáteresztő tükre az állítócsavarokkal közös foglalatban van, amit bármilyen szabványos felülvilágítós mikroszkóp-objektívre fel lehet szerelni. Célszerűen a 10x-es vagy 20x objektívre célszerű szerelni és a fényforrást monokromatikus fényt adó LED diódával vagy inkább spektrál lámpával kell helyettesíteni.
A csíktávolságot okulármikrométerrel lehet igen pontosan mérni szubjektíven vagy fotoelektromos úton objektíven.
A fennemlített hátrányai ellenére igen komoly előnye, hogy mindenféle-átlátszó vagy átlátszatlan-réteg esetében alkalmazható, a geometriai vastagságot adja, tehát nem kell ismerni a réteg törésmutatóját. A csík eltolódást a csíktávolság kb.l /20-ig elég jól le lehet olvasni illetve mérni. Így ha pl. 500 nm hullámhosszú fényt alkalmazunk, kb. 15 nm a mérhető alsó határ.
Vastagabb rétegek mérésénél nehéz a csík eltolódást nyomon követni, ezért előnyös, ha a réteg nem meredek falban végződik, hanem "lankás" az átmenet, ami megkönnyíti a csíkok követését.
Ilyen interferencia feltétet több optikai gyár is készít, ez bármely komolyabb mikroszkópra az előzőkben ismertetett módon felszerelhető és viszonylag olcsó. Egyes gyárak spektrállámpával, egybeépített komplett egységet is árulnak, amit az objektív és a tubus közé kell beszerelni.
Újabban Michelson-féle interferométert is alkalmaznak vastagságmérésre. Ez már célszerűen az u. n. interferencia mikroszkópba szilárdan be van építve. Hátránya, hogy a referenciatükör beállítása nehézkesebb, mint a F-P-é, viszont a tükör nem érintkezhet a réteggel és így az nem sérül meg.
Előnye a Michelson rendszernek, hogy a csíkok nem élesek, így azok fotometrálásával a feloldás fokozható, így a mérhető legkisebb vastagság 10 nm alatt van.
Az a.) alatt tárgyalt módszer, mint említettük átlátszó réteg esetében alkalmazható. Ha a hordozó fém, figyelembe kell venni a reflexió folyamán bekövetkező fáziseltolást is. Nagyobb tiltott távszélességgel rendelkező félvezetők (Si, GaAs, InP stb.) a közeli infravörös fényben (1-1,2 mm) átlátszóak, ezért ezek vastagságmérésére is alkalmas az a.) módszer azzal a megkötéssel, hogy a monokromátornak a közeli infrában is működnie kell és infravörös képátalakítót kell használni. Egyes optikai gyárak (pl. Perkin-Elmer) olyan reflexiós feltétet gyárt, mely legtöbb infravörös spektrofotométer sugármenetébe beiktatható, így a távolabbi infrában átlátszó kis sávszélességű anyagból készült réteg vastagsága is mérhető. Kis átmérőjű nyalábot használva, nem teljesen sík felületen is alkalmazható.
Régi-új eljárás, mely a rétegvastagságon kívül az optikai állandókat is meghatározza. Az alapgondolat Drudetől származik és tulajdonképpen minden készen volt, ami ma is alkalmazást nyer. Hogy évtizedekig nem terjedt el annak oka, hogy rendkívül sok számítást igényel. Igaz, hogy elemi, de hosszadalmas és fárasztó. [ 6.4.]
Mai általános elterjedése annak köszönhető főleg a félvezető technológia számára, mivel a korszerű számítógépek segítségével már nem olyan ijesztő az értékelés. Az eljárás azon alapszik, hogy egy adott felületről vagy rétegről — akár átlátszó, akár nem — reflektálódó fény polarizációs viszonyai megváltoznak a beesőhöz képest. A természetes fény általában elliptikusan polározott, tehát a beesési síkban rezgő komponens nagysága más, mint a merőlegesé. E kettő alkotja a polarizációs ellipszis nagy és kis tengelyének felét. Reflexiónál ezek aránya és fázisa megváltozik. Ha
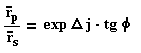
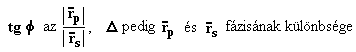
F és D bonyolult összefüggésben van a felület illetve réteg n, k törésmutató, kioltási tényező valamint a réteg vastagságával. Fés D mérésével a három előbbi mennyiségből kettő meghatározható. Harmadik mennyiség meghatározására még egy mérés szükséges pl. más beesési szög mellett.
A F , D és n, k, d kapcsolatok némileg egyszerűsödnek, ha a rétegre való beesés a fő beesési szögben történik (fő beesési szög esetében D=p/2). Mindhárom optikai mennyiség meghatározására azonban mindenképpen szükséges egy másik beesési szög is.
Az ellipszometer vázlata a (6.4. ábrán) látható.
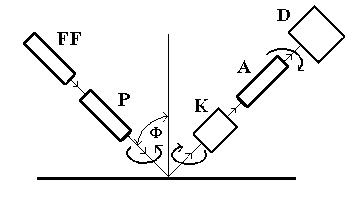
6.4. ábra
A monokromatikus fényt szolgáltató fényforrás (ma kizárólag lézer) kollimált fénye F szögben esik először a réteg nélküli hordozóra, amelynek n és k értékeit akarjuk meghatározni. A fény útjában álló P polarizátor lineárisan polározott fényt állít elő. A polarizáció síkja 45o-ot zár be a beesési síkkal. Az analizátort (A) úgy forgatjuk, hogy a D detektor minimális intenzitást mutasson. Ezután a K kompenzátort és az analizátort addig forgatjuk, míg a detektált intenzitás 0. A polarizátor és a kompenzátor valamint a polarizátor és analizátor közti szögből adódik F és D .
A főbeesési szöggel beeső fény polarizált, tehát elmaradhat a kompenzátor és mint szó volt róla, egyszerűsödnek a formulák is. E vázlatos ismertetés alapján is világos, hogy a mérés pontossága elsősorban a szögmérés pontosságán múlik. A hordozó optikai állandóinak illetve Fés D-nak ismeretében a mérést megismételjük immár a réteggel fedett hordozó esetében. Ekkor megkapjuk a réteg polarizációs állapotváltozását. A réteg reflexiós Fresnel együtthatóját írva a hordozóé helyébe, újabb hosszú számolás után megkapjuk immár a réteg két jellemzőjét. Ha a réteg átlátszó, n és d adódik. Az ellipszometria pontossága, mint már említettük a szögmérések pontosságán múlik.
Már Drude vizsgálataiból is kiderült, hogy a rétegvastagság alsó határa kb. 1 nm volt, + 0,3 nm pontossággal. A törésmutató értéke legalább 5 tizedesre pontos.
A korszerű ellipszometerek automatizáltak és a gyárak számítógépes programokat vagy grafikonokat mellékelnek a gyakrabban használt rétegek gyors vizsgálatához. Ismert rétegek esetében a számítás menete fordított: ismert n és k értékek mellett kiszámolják a különböző beesési szögekhez tartozó F és D értékeket illetve a számítható vastagságot. Korlátoltabb pontosság esetén F paraméterezésével diagramsereg készíthető és a mérés így rutinszerűvé, tehát üzemszerűen elvégezhetővé válik.
6.1.7. Alkalmazási lehetőségek
Félvezető technológiában SiO2, Si3N4 rétegek vastagságának és optikai állandókon keresztül összetételének vizsgálata. Kritikus alkalmazásokban fotoreziszt vastagságának meghatározása. Fotolitográfia ellenőrzése olyan értelemben, hogy a reziszt ábra maradéktalanul "kinyílt", azaz nem maradt e a megmunkálandó felületen igen vékony, esetleg túl polimerizálódott reziszt.
Ionmarások esetében, ahol a szelektivitás nem túl nagy, végpont detektorként alkalmazható in situ vizsgálatként. Itt a pontosság nem lényeges, csupán azt kell indikálni, hogy az eltávolítandó réteg optikai állandótól eltérő értékek adódnak, illetve az előre beállott értékektől hirtelen eltérés mutatkozik.
Révész és Zaininger [6.5.] GaAs-on kialakult oxidréteg tulajdonságait vizsgálta. Megállapították, hogy közvetlen előállítás után spontán növekedéssel mintegy 0,7 nm vastag oxid növekszik. Az is kiderült - ami logikus is -, hogy a törésmutató értéke jelentősen eltér a tömbanyagétól illetve vastag oxidétól. Vastagabb (d > 50 nm) rétegek vizsgálatából egyértelműen adódott, hogy az oxidáció folyamán a felületen arzén dúsul fel, és az oxid túlnyomóan As2O3. Hosszabb oxidációs folyamat alatt kialakul a Ga2 O3 szerkezetű galliumoxid is.
Ugyancsak a szerző páros vizsgálta a Si felületén kialakult spontán oxid vastagságát, valamint alumínium anódos oxidációja (plazmában) mechanizmusát.
Vasicek [6.6.] kiszámolta Is és Ip értékét n és k függvényében F = 0-80o közti beesési szögekre, ez igen hasznos kiegészítése az ellipszometriai számításoknak.
Keményrétegek vastagságának, részben szerkezetének megállapítására szintén előnyösen használható, gépelemek felületén létrehozott rétegek is vizsgálhatók.
Általánosságban elmondható, hogy az ellipszometria olyan optikai elven működő eljárás, mely anyagvizsgálatoknak is hasznos kiegészítője és ma már szinte minden területen nélkülözhetetlen.
Külön ki kell emelni, hogy igen kis felületű mintán elvégezhető a mérés. Ez a mindinkább terjedő nanotechnikában, ahol a méretek már mm alattiak, a rétegvastagságok egyre kisebbek, sokszor az atomréteg vastagságot alig haladják meg, a jövőben egyre nagyobb szerephez juttatja az ellipszometriát, hiszen más eszközökkel a szükséges vizsgálatok alig-alig végezhetők el.
Az eredeti Drude féle polarometriát Försterling némileg leegyszerűsítette a következő módon:
- Csak átlátszó hordozó esetén alkalmazható
- A réteg és hordozó levegővel érintkezik (n1 = n4 = 1)
- A fény beesése a réteg és a hordozó irányából szimmetrikusan történik.
Itt tehát nemcsak a reflexiós-, hanem a transzmissziós Fresnel együtthatókat is figyelembe kell venni. Maga a mérés ugyanúgy történik, mint az eredeti módszer alapján. Nagyon vékony rétegek esetében (d/l << 1) az eredetinél jóval egyszerűbb összefüggés adódik a vastagságra.
Ez a modern számítógépek korában nem számít nagy előnynek, viszont az, hogy az eredetihez képest más elrendezés szükséges és egyéb megszorítások is vannak, úgy tűnik, hogy ma már a módszer nem használatos.
Többen végeztek kisebb-nagyobb átalakításokat a mérés elméleti kiértékelésének egyszerűbbé tételére, ezek azonban olyan mértékű elhanyagolásokat tartalmaznak, melyek az eredeti koncepció igen nagy pontosságát kétségessé teszik. Ezért ezekkel az eljárásokkal ma már nem találkozunk.