|
Kezdőlap-Home
Page |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. évfolyam 4. szám 2001. október
[HUN] - Magyar cikk
|
1.fejezet.....
2. Kisciklusú fáradás A berendezések, szerkezetek, szerkezeti elemek, gépalkatrészek túlnyomó többségét ma is folyáshatárra méretezik, azok tervezésénél és gyártásánál azonban szükségszerűen keletkeznek feszültséggyűjtő helyek (például nyomástartó edények csőcsonkjainak környezete). A normál üzemeltetés során is felléphetnek olyan járulékos terhelések, amelyek a tervezéskor nem voltak ismertek, illetve nagyságuk nem volt számszerűsíthető (példaként említhetők az indítási és leállási folyamatok tranziens hatásaiból származó véletlenszerű terhelések). Egyértelmű tehát, hogy számolni kell egyes szerkezeti elemek, alkatrészek túlterhelésével, amelyek a szívós-képlékeny anyagok helyi képlékeny alakváltozását okozhatják. Amennyiben a túlterhelés csak egyszer fordul elő az a feszültségcsúcsok leépülését, a feszültségek átrendeződését, a képlékenyen alakváltozó anyag keményedését, és ezeken keresztül a teherbíróképesség növekedését eredményezheti. Abban az esetben, ha a kedvezőtlen hatások többször ismétlődnek, az anyagok alakváltozóképessége kimerülhet, kis számú igénybevétel után repedések keletkezhetnek, növekedhetnek végül töréshez vezethetnek. Ezt a jelenséget nevezzük kisciklusú fáradásnak [6, 7]. A Miskolci Egyetem (akkor még Nehézipari Műszaki Egyetem) Mechanikai Technológiai Tanszékén az 1980-as évek elejétől folyik a kisciklusú fáradás kutatása, amely egyaránt kiterjed a mikroszerkezeti folyamatok és a vizsgálattechnikai kérdések elemzésére. A diszlokációs folyamatok tanulmányozásának eredményeit bemutató publikációk közül a [8] és [9], azok modellezéséről készültek közül a [10] és a [11], a modellek és a fáradási jellemzők közötti kapcsolatokról szólók közül pedig a [10-15] számúakat emeljük ki. A másfél évtized alatt elvégzett nagyszámú, szisztematikus kisciklusú fárasztás alapján sok vizsgálattechnikai problémát oldottunk meg, különböző befolyásoló tényezők hatását elemeztük, amelyek közül a következő három területen elért eredményeket foglaljuk össze:
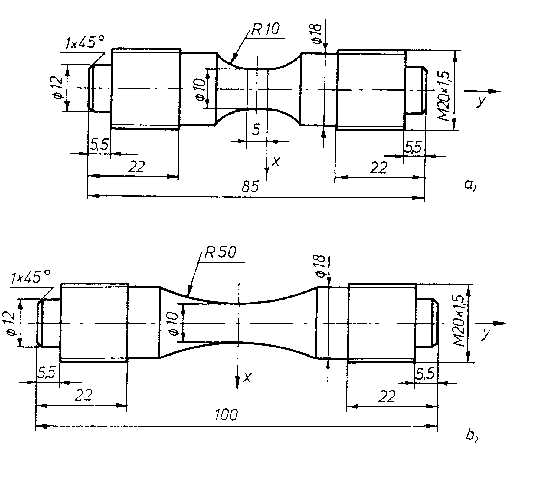
2.1. Kisciklusú fárasztási eredmények megbízhatósága, azonossága Minden új vizsgálati módszer bevezetése, alkalmazása esetén felmerül a kérdés: milyen a kapott mérési eredmények meghatározásának megbízhatósága? A kérdés megválaszolása érdekében az 1. ábrán látható két próbatest-típuson végzetünk vizsgálatokat. A próbatestek anyagául – a szövetszerkezeti inhomogenitások hatásának csökkentésére – X 12 CrNiTi 18 9 acélminőséget választottunk. A fárasztást három különböző teljes alakváltozás amplitúdóval (e a1=± 1,89%, e a2=± 0,94%, e a3=± 0,38%), terhelési szintenként 5-5 próbatesten, levegőn, szobahőmérsékleten, törésig végeztük. A különböző teljes alakváltozás amplitúdójú fárasztással kapott törési ciklusszámok (Nt), továbbá az élettartam 50%-ához tartozó feszültségamplitúdók átlagát, szórását és variancia együtthatóját az 1. táblázat mutatja.
1. ábra: Vizsgált próbatest-típusok
1. táblázat: Különböző próbatesttípusok esetén meghatározott jellemzők
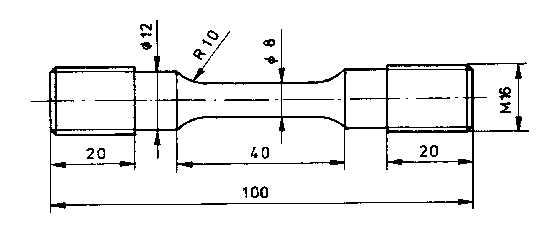
Az 1. táblázat adatai alapján a következő megállapítások tehetők [16]: a törési ciklusszámok szórása, variancia együtthatója meghaladja a statikus mechanikai mérőszámoknál szokásos értékeket, de lényegesen kisebbek a nagyciklusú fárasztásnál észlelteknél; az élettartam 50%-ához tartozó feszültségamplitúdók (s a50) szórásai, variancia együtthatói jól megegyeznek a szakítóvizsgálatnál meghatározott szakítószilárdság és folyáshatár meghatározásánál tapasztaltakkal; a törési ciklusszámok átlagának eltérése, szórása és variancia együtthatója csökken az alakváltozási amplitúdó növekedésével. 2.2. A mérési eredményeket befolyásoló vizsgálattechnikai tényezők és hatásuk A mérési eredményeket egyrészt vizsgálattechnikai tényezők, másrészt az állapottényezők befolyásolják. A legfontosabb, első csoportba sorolható tényezők a következők [17]: a vezérelt változó beállításának pontossága, reprodukálhatósága; az alkalmazott nyúlásmérő fajtája (hossz- vagy keresztirányú nyúlásmérő); a próbatestek alakja és mérete; a próbatestek felületi minősége; a terhelés aszimmetria tényezője; a terhelési függvény alakja; a tönkremeneteli kritérium. A kisciklusú fárasztás eredményeit meghatározó módon befolyásolja a vezérelt változó, az alakváltozás amplitúdó szabályozásának pontossága. Mivel a gyakorlatban hossz- és keresztirányú nyúlásmérőket is alkalmaznak, és a kétféle mérőeszköz esetén nem szükségszerű a szabályozás pontosságának azonossága, célszerű a két kérdéskört összekapcsolni. Tekintettel arra, hogy a szabályozás pontossága az alakváltozás amplitúdó nagyságától is függhet, a vizsgálatokat különböző alakváltozás amplitúdókkal kívánatos elvégezni. A szabályozás pontosságának elemzésére olyan kísérletsorozatot terveztünk, amelynél azonos anyagból (C10) készült, a 2. ábrán látható 5-5 próbatesten, hossz- és keresztirányú nyúlásmérővel is végeztünk vizsgálatokat [18].
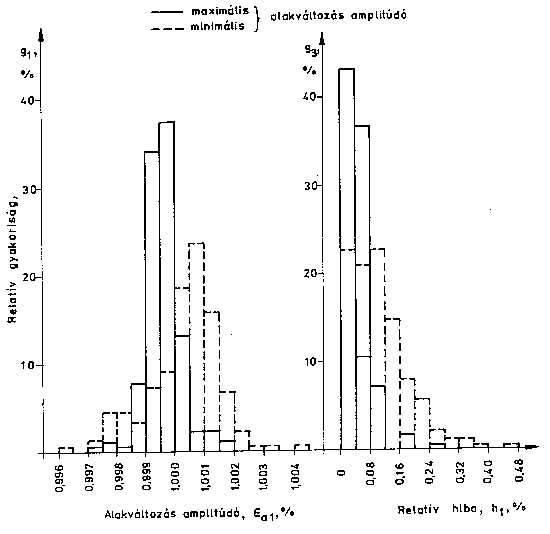
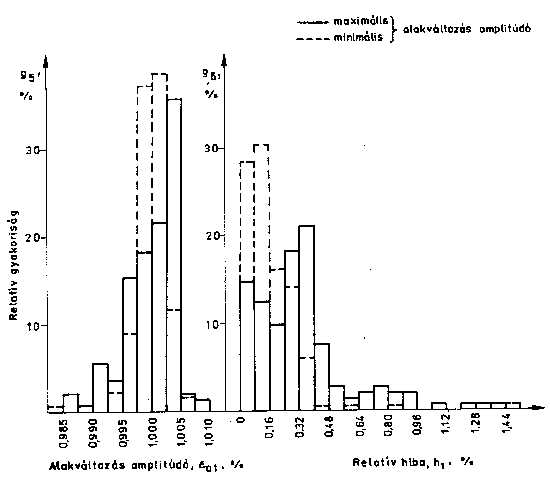
2. ábra: Kisciklusú fárasztó próbatest hossz- és keresztirányú nyúlásmérőkhöz A kisciklusú fárasztást két, állandó maximális alakváltozás amplitúdóval (e a1=± 1%, illetve e a2=± 0,5%), R=-1 aszimmetria tényezővel a maximális húzóerő 25%-os csökkenéséig végeztük, számítógéppel vezérelt MTS gyártmányú berendezésen, miközben regisztráltuk az alakváltozás amplitúdók minimális és maximális értékét minden tizedik ciklusnál. A hosszirányú nyúlásmérő mérőhossza 10 mm volt. A keresztirányú nyúlásmérővel végzett vizsgálatoknál az alakváltozás amplitúdót hosszirányú értékre számítottuk át [19], az összehasonlíthatóság érdekében. A kísérletekbe bevont, azonos feltételekkel fárasztott próbatesteken mért mintegy 200-200 maximális és minimális alakváltozás amplitúdó értékeket intervallumokra osztottuk és megrajzoltuk a relatív gyakorisági hisztogramjaikat [20]. Kiszámítottuk minden alakváltozás amplitúdó maximális és minimális értékeinek relatív hibáját, amiket szintén oszlopdiagramokban ábrázoltunk [21]. A mérési eredményhalmazból három csoportot mutatunk be a fontosabb következtetések érzékeltetésére. A 3. ábra az előzőkben ismertetett oszlopdiagramokat mutatja be hosszirányú nyúlásmérőre és e a1=± 1%-os alakváltozás amplitúdóra, a 4. ábra ugyanezt szemlélteti, csak e a2=± 0,5% esetén [22]. A keresztirányú nyúlásmérővel, e a1=± 1%-os alakváltozás amplitúdóval végzet vizsgálatokra vonatkozó értékek a 5. ábrán láthatók
3. ábra: Alakváltozás amplitúdó és relatív hibájának gyakorisági hisztogramjai e a1=± 1% és hosszirányú nyúlásmérő esetén
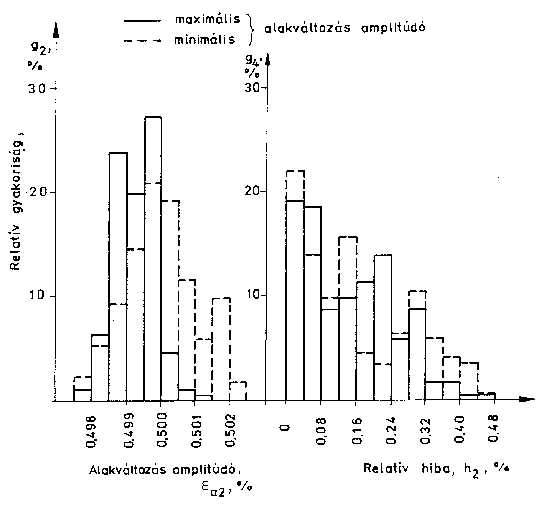
4. ábra: Alakváltozás amplitúdó és relatív hibájának oszlopdiagramjai e a2=± 0,5% és hosszirányú nyúlásmérő esetén
5. ábra: Alakváltozás amplitúdó és relatív hibájának gyakorisági hisztogramjai e a1=± 1% és keresztirányú nyúlásmérő alkalmazásánál Az eredmények alapján a következő főbb megállapítások tehetők [18, 22]:
Meg kell jegyezni, hogy az előző megállapítások az adott berendezésre, mérőrendszerre érvényesek. Mivel az egyes gépek, műszerek pontossága nem feltétlenül azonos, az előző vizsgálatokat célszerű minden laboratóriumban elvégezni. A próbatest alakját, méretét alapvetően meghatározza annak a terméknek az alakja és mérete, amelyből a próbatest kimunkálásra kerül. Az alak megválasztásánál fontos az is, hogy a rendszerint húzó-nyomó terheléssel fárasztott próbatestek ne hajoljanak ki. Ezért a kisciklusú fárasztó próbatestek többsége zömök [19], bár alakjuk eltérhet egymástól. A legfontosabb típusokat, méretarányaikkal együtt a [24] és a [16] közlemények összefoglalták. Az egyik típusnál a kihajlási veszély csökkentése érdekében a vizsgált rövid hengeres részt a lényegesen nagyobb fejjel rádiusz közi össze. A másik típusnál hiányzik az állandó keresztmetszetű szakasz, a próbatest felülete tórusz. Joggal tehető fel a kérdés, hogy e két típusú próbatesten meghatározott mérőszámok azonosnak tekinthetők-e? A kérdés megválaszolásához felhasználhatók a kisciklusú fárasztási eredmények megbízhatóságának elemzésére kapott eredmények, amelyeket az 1. ábrán látható próbatesteken mértünk. A különböző anyagi mérőszámok halmazának azonosságát ebben az esetben is Wilcoxon-próbákkal vizsgáltuk, amelyek eredményeit figyelembe véve a következő megállapítások tehetők:
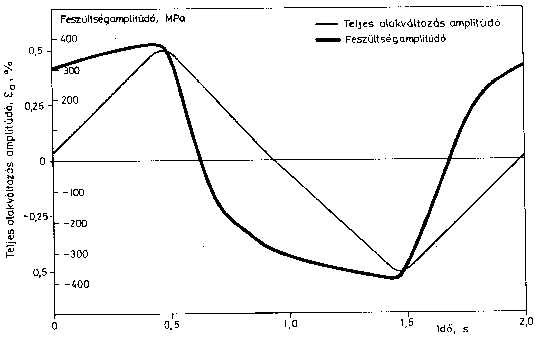
A kisciklusú fárasztó próbatestek mérete a leggyakrabban alkalmazott mérettartományban, ami hengeres próbatesteknél d0=5 mm-től d0=20 mm-ig terjed [25], nincs lényeges hatással a mérési eredményekre. A szokásos méretektől lényegesen nagyobb átmérők alkalmazása különlegesen nagy teljesítményű berendezést kívánna meg, ami miatt alkalmazásuk ritka, kevés mérési eredmény ismert. Külön célszerű elemezni a próbatestek felületének minőségét. Amennyiben ezt a fogalmat komplexen értelmezzük, azaz abba a felületi érdességen túl a felületi réteg fémtani és feszültségállapotát is beleértjük, biztosan lényeges hatással van a kisciklusú fárasztás eredményeire. Tekintettel arra, hogy a felületi réteg fémtani és feszültségállapotát rendszerint olyan technológiák alkalmazásával változtatják meg, amelyek egyszerre mindkét állapotot módosítják (termokémiai kezelések, felületgörgőzés stb.), hatásukat külön-külön rendkívül nehéz elemezni. A felületi érdesség hatása – a nagyciklusú fárasztásnál tapasztaltakkal ellentétben – elhanyagolható [24], mivel a viszonylag nagy képlékeny alakváltozás már az első terhelésnél eltünteti azokat a mikroszkópi méretű egyenetlenségeket, amelyekből a kis terheléseknél, nagy élettartamoknál a repedések kiindulnak. Kisciklusú fárasztásnál, amelyet rendszerint teljes alakváltozás amplitúdóra vezérelnek [26] az aszimmetria tényező értéke pedig -1£ R< 1 között változhat. A törésig elviselt igénybevételi szám az aszimmetria tényező növekedésével nő. Tehát a biztonság irányában tévedünk, ha a kedvezőbb aszimmetria tényezőjű terheléseknél is az R=-1-el meghatározott mérőszámokat alkalmazzuk. Ezért az kisciklusú fárasztóvizsgálatok többségét R=-1 értékű aszimmetria tényezővel végzik [27]. A terhelési függvény alakjának hatása előre becsülhető abból az ismert tényből kiindulva, hogy a képlékeny alakváltozásra jellemző feszültség-nyúlás görbe az előélettől [28, 29], azaz az előző terhelés jellegétől, nagyságától, tehát a terhelési függvény alakjától függ. E hatást úgy kívántuk kimutatni, hogy a hagyományosan alkalmazott szinusz alakú terhelési függvény mellett háromszög, négyszög és trapéz alakú terhelési függvénnyel is végezünk kisciklusú fárasztást. A vizsgálatokra kazánok és nyomástartó edények gyártásához használt KL 7D jelű acélminőségen került sor. A vezérelt változó a teljes alakváltozás amplitúdó volt, amelynek értékét 0,5%-ra és 1%-ra választottuk. A két érték a szokásos kisciklusú fárasztási tartomány alsó és felső harmadába esik, az aszimmetria tényező R=-1 volt. Mindhárom terhelési függvénnyel és mindkét alakváltozási amplitúdóval 5-5 próbatestet fárasztottunk, szobahőmérsékleten. A vizsgálat során regisztráltuk a teljes alakváltozás- és feszültségamplitúdók időbeli változását, amelyekből a 6. ábrán – példaként – egy 0,5%-os, háromszög terhelési függvényű diagramot mutatunk be.
6. ábra: A teljes alakváltozás és feszültségamplitúdó időbeli változása egy ciklus alatt Minden sorozatnál meghatároztuk a tönkremeneteli ciklusszámok (Nt) és az élettartam 50%-ához tartozó feszültségamplitúdók (s a50) átlagát, szórását, továbbá a teljes alakváltozás amplitúdók mellett a rugalmas és a képlékeny alakváltozás amplitúdók átlagát is (2. táblázat). 2. táblázat: A terhelési függvény alakjának hatása a mért jellemzőkre
A különböző terhelési függvénnyel meghatározott jellemzők azonosságát ebben az esetben is Wilcoxon-próbával ellenőriztük. Az eredmények alapján a következő megállapítások tehetők: az 1%-os teljes alakváltozás amplitúdóval végzett fárasztás esetén a tönkremeneteli ciklusszámok (Nt) és az élettartam 50%-ához tartozó feszültségamplitúdók (s a50) 95%-os szignifikanciaszinten különbözőnek tekinthetők; a 0,5%-os teljes alakváltozás amplitúdóval végzett fárasztásnál a függvényektől függetlenül mind az élettartamok, mind a feszültségamplitúdók 95%-os szignifikanciaszinten azonosak, azaz egy-egy halmaznak tekinthetők [30]. A mérési eredmények e látszólagos ellentmondása feloldható, ha a rugalmas és a képlékeny alakváltozás amplitúdók nagyságát is elemzzük. Az 1%-os teljes alakváltozás amplitúdójú vizsgálatoknál a képlékeny alakváltozás amplitúdók nagysága majdnem négyszeres a rugalmas alakváltozás amplitúdókénak, kifejtve a tönkremenetel szempontjából domináns képlékeny alakváltozás jelentőségét, érvényre juttatva a terhelési függvényalak hatását. Ezzel szemben a 0,5%-os teljes alakváltozás amplitúdójú vizsgálatok esetén a képlékeny alakváltozás amplitúdók még a rugalmas alakváltozás amplitúdók kétszeresét sem érik el. Ebben az esetben a reverzibilis rugalmas és az irreverzibilis képlékeny alakváltozás összemérhető, csökkentve az utóbbi hatásának érvényesülését, elmosva a terhelési függvény alakjának hatását [17, 31]. A kisciklusú fárasztóvizsgálatok végének megállapítására különböző tönkremeneteli kritériumokat alkalmaznak. Fizikailag leginkább megalapozott az a felfogás, amelynél a terjedőképes repedés megjelenését tekintik a vizsgálat végének. Ugyanakkor nehéz meghatározni és mérni a repedés ezen méretét. Ezért a gyakorlatban az előző helyett a közvetkező tönkremeneteli kritériumokat alkalmazzák [24, 26]:
E sokféle törési kritérium hatásának szisztematikus elemzésére még nem került sor, csupán néhány tényező, például az erőcsökkenés 10%-os és 25%-os értékének összehasonlítására vannak részeredmények [17].
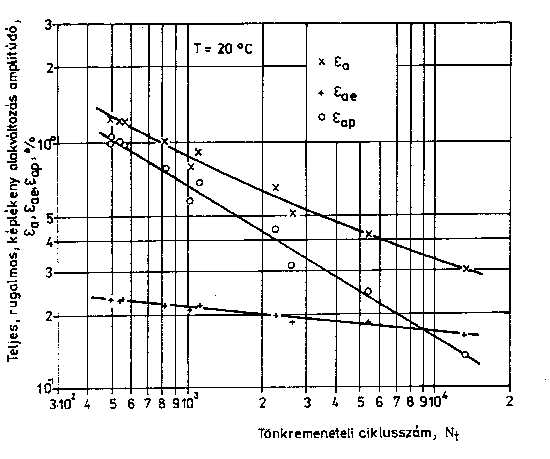
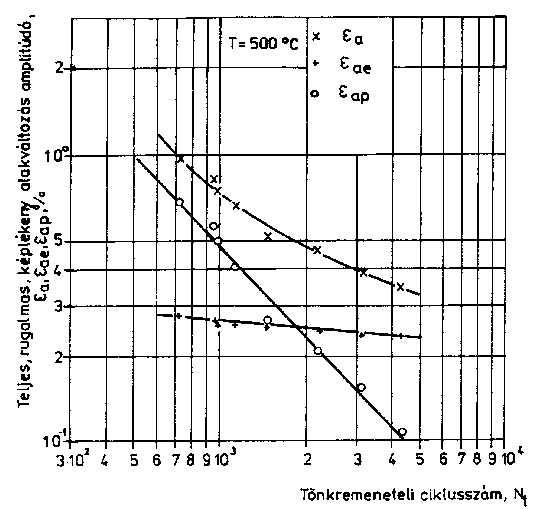
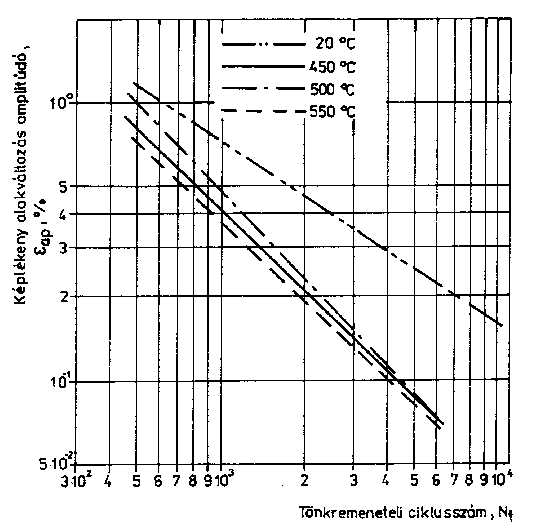
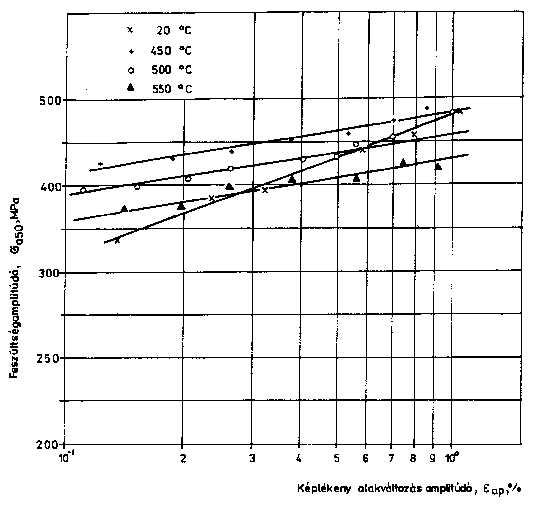
2.3. Az állapottényezők hatása A fémek és ötvözetek tulajdonságát azok összetételén, fémtani állapotán túl az állapottényezők is befolyásolják. A felhasználás szempontjából előnyös ismerni az állapottényezők kisciklusú fárasztás eredményeire gyakorolt hatását is. Az egyik állapottényező, az alakváltozási sebesség jelentős mértékben az igénybevételi sebességtől, illetve az átlagos igénybevételi sebességtől, vagy a mérésnél gyakrabban használt fárasztási frekvenciától függ. A jelenleg alkalmazott méréstechnikai feltételek mellett a vizsgálati frekvencia kisciklusú fárasztásnál viszonylag szűk tartományban változtatható, maximum egy nagyságrendet fog át (néha tized Hz-től néhány Hz-ig terjed) [27]. Ilyen feltételek mellett az alakváltozás sebességének hatása érdemben nem elemezhető. A másik állapottényező a feszültségállapot, amelynek hatása különböző módszerekkel tanulmányozható. Ezek közül a legegyszerűbben megvalósítható a bemetszett próbatestek vizsgálata. Ebben az esetben a próbatest feszültség- és alakváltozás állapota inhomogén lesz, ami megnehezíti a megbíz ható következtetések levonását [32, 33]. A másik lehetőség, hogy bonyolultabb vizsgáló berendezések alkalmazásával állítják elő a többtengelyű feszültségállapotot [33, 34]. A bonyolultabb és ezért kisebb számban végrehajtott ilyen vizsgálatok ma még nem tesznek lehetővé általánosítható, mennyiségi megállapításokat, bár úgy tűnik, hogy az egyenértékű alakváltozás alapján a mérési eredmények összevonhatók [35].A harmadik állapottényező, a hőmérséklet, hatásának kimutatására végzett vizsgálatok jelentős számban előfordulnak a közleményekben [27]. Mi többféle acélon tanulmányoztuk a hőmérséklet hatását, az eredménye közül a KL 9 acélminőségen mért adatokat mutatjuk be. A 7. ábrán a 20° C-os, a 8. ábrán pedig az 500° C-os mérés alakváltozás amplitúdók-tönkremeneteli ciklusszámok kapcsolata látható. A Manson-Coffin egyeneseket, különböző hőmérsékleteknél, a 9. ábra, a képlékeny alakváltozás amplitúdó-feszültségamplitúdó kapcsolatát pedig a 10. ábra szemlélteti [36]. Az eredmények alapján a következő, fontosabb megállapítások tehetők: az élettartam és a képlékeny alakváltozás amplitúdó közötti kapcsolat jelentősen eltér a 20° C-os és a 450° C-os, 500° C-os, illetve 550° C-os méréseknél; a növelt, különböző hőmérsékletű méréseknél a képlékeny alakváltozás amplitúdó csökkenésével csökken a tönkremeneteli ciklusszámok különbsége; a vizsgálati hőmérséklet növekedésével csökken a ciklikus folyásgörbe meredeksége, a keményedési kitevő, ami az alakítás és a hőmérséklet hatására bekövetkező összetett anyaszerkezeti változásokkal függ össze.
7. ábra: A KL 9 jelű acélon vézzett mérések eredményei 20° C-on
8. ábra: A KL 9 jelű acélon végzett vizsgálatok eredményei 500° C-on
9. ábra: A KL 9 acélminőség Manson-Coffin egyenesei különböző hőmérsékleteken
10. ábra: A KL 9 acélminőség ciklus folyásgörbéi
Irodalmi adatok és ezen eredmények felhasználásával készültek azok a fizikai modellek, valamint ellenőrző számításaik, amelyekre a korábbiakban – a [10, 11] hivatkozásoknál – már utaltunk. A növelt hőmérsékletű vizsgálatoknál külön meghatároztuk a tönkremenetelig befektetett munkák értékeit. Azt tapasztaltuk, hogy az alakváltozás amplitúdóktól, a mérések szórásától eltekintve, függetlenek a munkák értékei, ugyanakkor jelentős mértékben változnak a vizsgálati hőmérséklet függvényében [37, 38]. A törésig befektetett munkák átlagát a 2. táblázatban foglaltuk össze. 2. táblázat: A vizsgálati hőmérséklet és a befektetett munka kapcsolata
A meghatározott munkák szórása, variancia együtthatói megfelelnek a fajlagos törésmunka mérésénél tapasztaltaknak.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||