|
Kezdőlap-Home
Page |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. évfolyam 4. szám 2001. október
[HUN] - Magyar cikk
|
2.fejezet.....
3. Fáradásos repedésterjedés A különböző gépészeti szerkezetek tönkremenetelének, törésének leggyakoribb oka a fáradás, s ez leggyakrabban a hegesztett szerkezetek körében fordul elő [39]. Az, hogy egy szerkezet élettartamát alapvetően a mikrorepedések keletkezéséig eltelt idő vagy a repedésterjedési szakasz határozza-e meg, illetve mindkettő egyaránt fontos, függ az alkalmazott anyagoktól, a konstrukciótól és az igénybevételtől, valamint a szerkezet gyártástechnológiájától [40]. A két eset kombinációjával leggyakrabban szintén a hegesztett szerkezeteknél találkozhatunk. A fáradásra való méretezésnek alapvetően két koncepciója ismeretes [41, 42]. A biztos élettartamra való (safe-life) méretezés azt feltételezi, hogy a szerkezet hibamentes, illetve ha tartalmaz hibát, akkor abból terjedőképes repedés nem keletkezik. Ez azt jelenti, hogy a méretezéskor figyelembe vett körülmények között katasztrofális törés nem következik be és a szerkezeti elem cseréjére sem kerül sor a tervezett élettartam lejárta előtt. A másik koncepció, a sérülésbiztos (fail-safe) méretezés, azon a felfogáson alapul, hogy a szerkezetekben eleve vannak, vagy annak üzemeltetése során keletkeznek repedések, s ezek a repedések növekednek. Ezen elv szerint a szerkezetnek a hiba sorsáról való döntés meghozataláig viselnie kell a terhelést. A sérülésbiztos méretezési filozófia alkalmazása más üzemeltetési stratégiát, magatartást kíván, mint a biztos élettartamra való méretezés koncepciója. Az üzemeltetés során folyamatos és/vagy időszakos ellenőrzéseket kell végezni, s azok eredményeit értékelve kell a hogyan tovább-ra vonatkozó döntést meghozni Egyértelműen kimondható tehát, hogy hangsúlyos szerepe van azoknak a témaköröknek, amelyek a fáradási károsodás mind egységesebb és teljesebb leírásával, a sérülésbiztos méretezési koncepció alkalmazásával, az anyagi mérőszámok valós terhelési viszonyok esetén érvényes értékeinek meghatározásával, illetve az üzemelő szerkezetek megbízhatóságával foglalkoznak. Mindezeket figyelembe véve a fáradásos repedésterjedés témakörében a következő területeken elért eredményeket emeljük ki:
a terhelési ciklusalak fáradásos repedésterjedésre gyakorolt hatása.
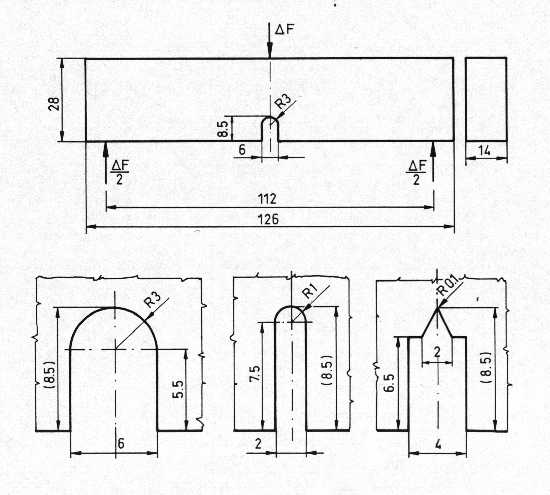
3.1. A repedéskeletkezési ciklusszám meghatározása A fáradási károsodás, a teljes törési folyamat leírására vonatkozó törekvések igénylik a repedéskeletkezési ciklusszámra vonatkozó vizsgálatokat is [43]. Tekintettel arra a tényre, hogy a repedések keletkezésében a feszültséggyűjtő helyeknek döntő szerepe van [39], az ilyen típusú vizsgálatokat gyakran végzik bemetszett próbatesteken [44, 45]. A különböző mérési módszerek közös vonása az, hogy az anyagvizsgáló berendezés speciális eszközzel való kiegészítését igénylik [46]. A bemetszés lekerekítési sugarának repedés keletkezésére gyakorolt hatása ismert, kevésbé tisztázott viszont annak a fáradásos repedés (további) terjedésével való kapcsolata [47, 48]. A kutató munka során ismétlődő igénybevétel esetére kialakítottuk a repedéskeletkezési ciklusszám meghatározásának a bemetszésen mért szétnyílás regisztrálásán alapuló módszerét. A vizsgálatok során a megszokott helyen elhelyezett, általános célú szétnyílásmérő jelét (erő-szétnyílás) kell rögzíteni meghatározott igénybevételi ciklusonként. A kapott görbékből szétnyílás maximum-igénybevételi ciklusszám függvények szerkeszthetők, s a szétnyílás monoton növekedéséhez tartozó pontból a repedéskeletkezési ciklusszám kijelölhető. A módszer alkalmazhatóságát azonos anyag és három különböző bemetszés-geometria, majd azonos bemetszés-geometria és három különböző anyagminőség esetén igazoltuk. A vizsgálatokhoz alkalmazott próbatestek TPB [49, 50] típusúak voltak. A különböző bemetszés-geometriájú (r=0.1 mm, r=1 mm, r=3 mm) próbatestek 10 Cr Mo 9 10 jelű acél alapanyagból és annak hegesztett kötéseiből készültek, orientációjuk L-R és 2-3 volt [49, 50]. A bemetszések geometriáját a 11. ábra szemlélteti.
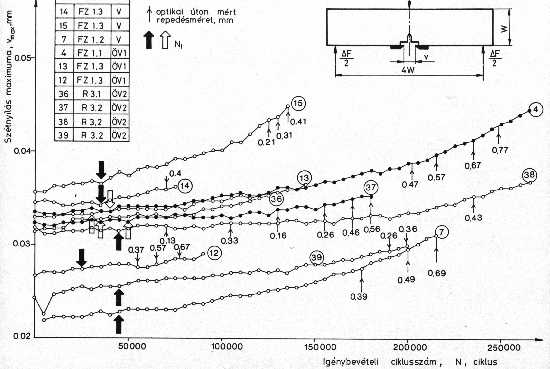
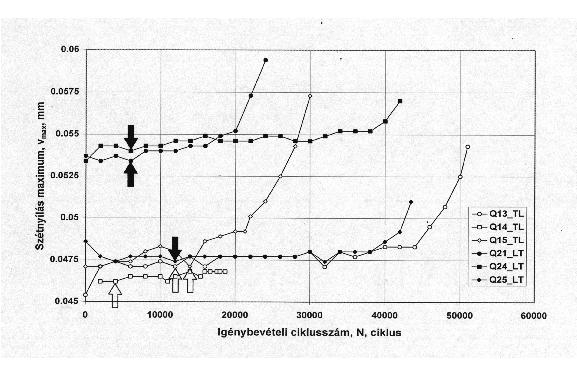
11. ábra: A repedéskeletkezési ciklusszám vizsgálatához alkalmazott bemetszések geometriája a 10 Cr Mo 9 10 jelű acél és hegesztett kötései esetén Az r=0.1 mm-es lekerekítési sugarú, hegesztett kötésekből készült próbatestek szétnyílás maximum-igénybevételi ciklusszám (vmax-N) görbéit a 12. ábra foglalja össze, s azon az optikai úton mért repedésméretek, valamint a repedéskeletkezési ciklusszámok (Ni) is szerepelnek.
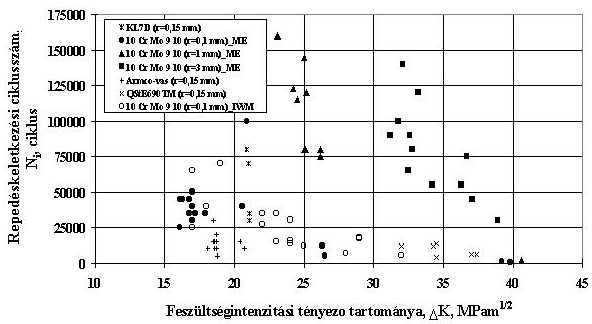
12. ábra: Szétnyílás maximum–igénybevételi ciklusszám görbék a 10 Cr Mo 9 10 acél hegesztett kötésein elvégzett vizsgálatokra (r=0.1 mm) Az azonos bemetszés-geometriájú (r=0.15 mm) próbatestek Armco-vas, KL7D és QStE690TM jelű acél alapanyagokból készültek. Az Armco-vas esetében az orientáció L-T, a KL7D jelű acélnál L-S, a nagyszilárdságú acél vizsgálatainál pedig T-L és L-T volt. Az utóbbi acél esetében kapott eredményeket a 13. ábra mutatja. 13. ábra: Szétnyílás maximum-igénybevételi ciklusszám görbék a QStE690TM jelű acél alapanyagon elvégzett vizsgálatokra (r=0.15 mm) Az összes, minden anyagon és minden repedésgeometria esetén meghatározott repedéskeletkezési ciklusszámot a 14. ábra szemlélteti, amelyen szerepelnek a Fraunhofer Institut für Werkstoffmechanik Freiburg-ban, más módszerrel [51] kapott eredmények is. Az ábra – a miskolci és a freiburgi eredmények jó egyezősége mellett – megerősíti azt a két, szemléletünkkel összhangban lévő tényt, hogy azonos névleges sugarú bemetszések esetén a feszültségintenzitási tényező tartományának növekedése a repedéskeletkezési ciklusszám csökkenését vonja maga után;azonos feszültségintenzitási tényező tartomány esetében a kisebb névleges sugarú bemetszéshez tartozik a kisebb repedéskeletkezési ciklusszám.
14. ábra: A repedéskeletkezési ciklusszám vizsgálatok eredményei
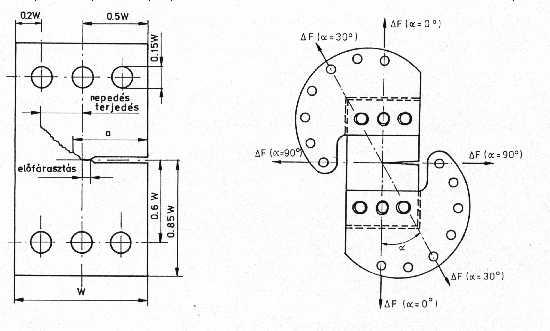
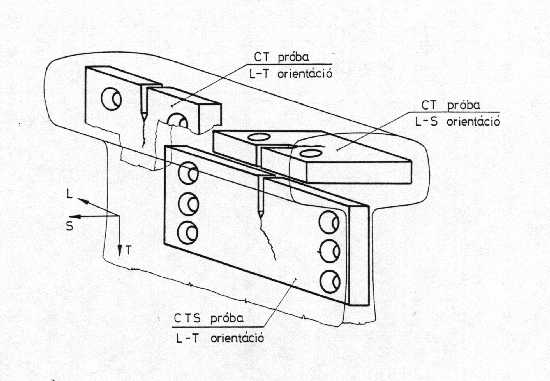
3.2. Fáradásos repedésterjedés összetett igénybevételi módban Az összetett igénybevételi módú problémák elemzésére több törési kritérium [52, 53, 54] áll rendelkezésre, amelyek meghatározzák a fáradásos repedésterjedés leírására alkalmazható modellt is. Említést érdemel, hogy az elveikben eltérő kritériumok közül több alkalmazza a fáradásos repedésterjedés Paris-Erdogan modellre [55] épülő leírását. Az ilyen típusú kvázistatikus és ismétlődő igénybevételű vizsgálatok karakterisztikus eltéréseket hordoznak a leggyakoribb, I terhelési módban elvégzett vizsgálatokhoz képest [40, 56, 57], kisebb azok megbízhatósága [58], s ebből következően nagyobb az élettartambecslés bizonytalansága. A kutató munka keretében megterveztük és megvalósítottuk a fáradásos repedésterjedés összetett igénybevételi módban (I+II) történő vizsgálata metodikájának egy lehetőségét. Megterveztük és legyártottuk a szükséges (befogó) készülékeket, kialakítottuk a terjedő repedés követésének és a mérési adatok kiértékelésének módszerét. Vasúti sínből készült próbatestek I+II igénybevételi módban elvégzett vizsgálatai alapján megállapítottuk, hogy az összetett igénybevételi módban terjedő repedésekkel szemben a sín eltérően viselkedik, attól függően, hogy a repedés a sín fejében vagy gerincében terjed. Megállapítottuk továbbá, hogy az összetett igénybevételi módban terjedő repedésekkel szemben a sín akkor is eltérően viselkedik, ha a repedés annak ugyanabban a részében, de a hossztengelyhez képest különböző irányokban terjed. Két anyagminőség (vasúti sín, nagyszilárdságú termomechanikusan kezelt acél) esetében, a próbatestek kimunkálása és a repedésterjedés irányának megválasztása segítségével olyan mérési eredménysorhoz jutottunk, amely megteremtette az összetett igénybevételi módra érvényes tervezési görbék meghatározásának lehetőségét. A részleteket a 3.3. fejezetben mutatjuk be. A vizsgálatokhoz alkalmazott próbatestek CTS (compact tension shear) típusúak voltak, a befogásukhoz tervezett és gyártott készülék pedig olyan, amely I (a =0° ), I+II (0° <a <90° ) és II (a =90° ) igénybevételi módban egyaránt alkalmas vizsgálatok végrehajtására [59, 60]. A próbatestet, a készülék alakját, a befogás módját és az a szög értelmezését a 15. ábra mutatja.
15. ábra: A CTS próbatest és vizsgálati lehetőségei A próbatestek előfárasztását I igénybevételi módban végeztük, az előfárasztási repedésméretet pedig 0.5W névleges értékben rögzítettük. A
alakú Paris-Erdogan összefüggés C és n állandóját az effektív feszültségintenzitási tényező tartománya [61] segítségével határoztuk meg:
Az összefüggésben szereplő k értéket [62] alapján k=1.28-ra választottuk, D KI és D KII értékét pedig az alábbi összefüggésekkel [54, 60] számítottuk:
A DO76 anyagminőségű vasúti sínből kimunkált próbatestek orientációja L-T, illetve L-S volt [63], amelyet a 16. ábra szemléltet.
16. ábra: A próbatestek elhelyezkedése és orientációja a sínben Az elvégzett vizsgálatok legfontosabb adatait és eredményeit a 3. táblázat foglalja össze. 3. táblázat: A DO76 jelű sínacélon elvégzett vizsgálatok legfontosabb adatai és eredményei
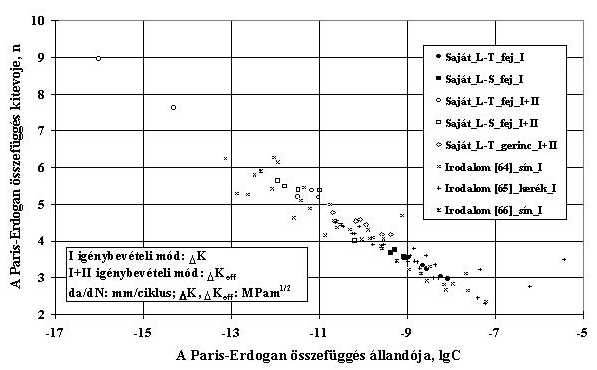
A korábbiakban megfogalmazottak mellett említést érdemel, hogy a Paris-Erdogan összefüggés kitevője (n) abban az esetben a legnagyobb, amikor a repedés abban az irányban terjed, amely a sín hossztengelyével leginkább egyező. A I+II igénybevételi módban kapott eredmények jó összhangban vannak a I igénybevételi mód esetén kapott saját és irodalmi [64, 65, 66] adatokkal, amelyet a 17. ábra mutat be.
17. ábra: A vasúti sínen végzett saját vizsgálatok összevetése irodalmi adatokkal A QStE90TM jelű termomechanikusan kezelt HSLA acélból kimunkált próbatestek T-L és L-T orientációjúak voltak. Az elvégzett vizsgálatok legfontosabb adatait és eredményeit a 4. táblázat foglalja össze. 4. táblázat: A QStE690TM jelű acélon elvégzett vizsgálatok legfontosabb adatai és eredményei
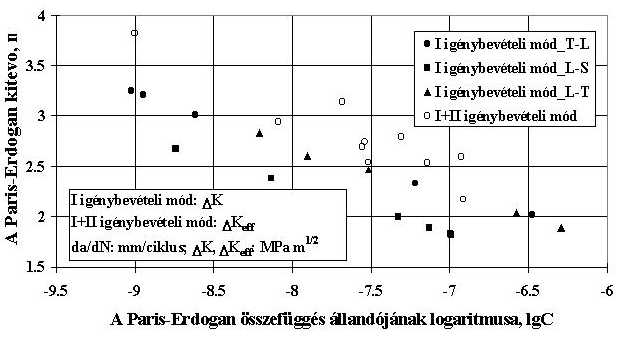
A I+II igénybevételi módban kapott eredmények ennél az anyagminőségnél is jó összhangban vannak a I igénybevételi módban elvégzett saját vizsgálatok eredményeivel, összhangban vannak a I igénybevételi módban elvégzett saját vizsgálatok eredményeivel, ahogy azt a 18. ábra szemlélteti.
18. ábra: A QStE690TM jelű acélon elvégzett vizsgálatok összehasonlítása A 3. és a 4. táblázatok, valamint a 17. és a 18. ábrák alapján megállapítható, hogy a I+II igénybevételi módban kapott Paris-Erdogan kitevő értékek alkalmasak tervezési görbék meghatározására.
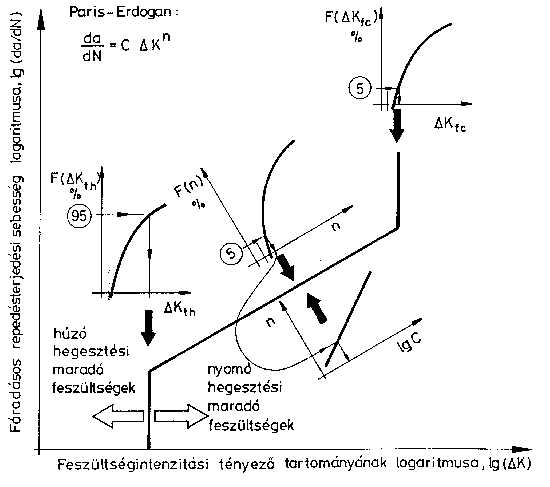
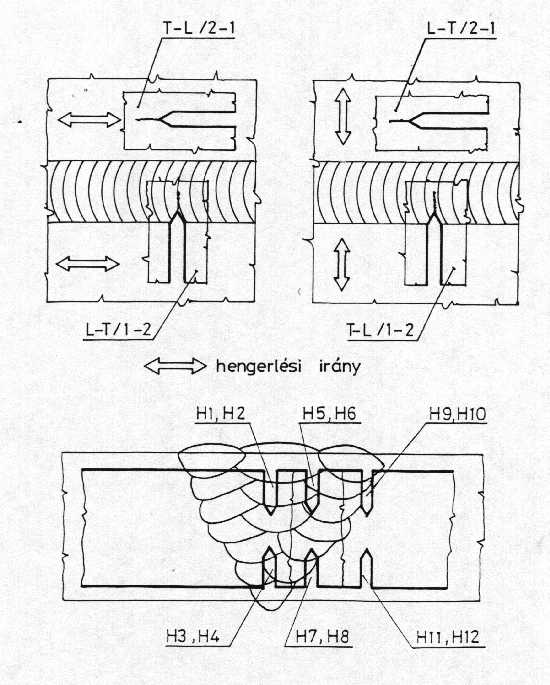
3.3. Tervezési görbék fáradásos repedésterjedésre Fáradásos repedésterjedésre érvényes tervezési görbéket több előírás [67, 68, 69, 70] és több irodalmi ajánlás [71, 72] is tartalmaz. E görbéket és származtatásukat összehasonlítva négy következtetés érdemel hangsúlyozást. Az első az, hogy mindegyik görbe a fáradásos repedésterjedés kinetikai diagramját egyszerűsítve közelíti meg, s a legelterjedtebb a Paris-Erdogan modellre [55] épülő megoldás. A második az, hogy a görbék I igénybevételi módra vonatkoznak, harmadszor pedig szembetűnő, hogy a javaslatok a nagy repedésterjedési sebességek tartományában nem alkalmaznak korlátozásokat. A negyedik lényeges következtetés az, hogy mindegyik görbe statisztikailag kezelhető mennyiségű kísérleti és/vagy irodalmi adatra épül, ugyanakkor egyik sem veszi számba az egyes mérőszámokat az élettartamra, illetve élettartambecslésre gyakorolt hatásuk szemszögéből. A [73] értekezésben összefoglalt munka folytatásaként - nagyszámú vizsgálat elvégzése és eredményeinek feldolgozása után - fáradásos repedésterjedésre érvényes tervezési görbéket határoztunk meg öt újabb acél alapanyag és közülük három hegesztett kötései, ausztemperált gömbgrafitos öntöttvas, továbbá három alumíniumötvözet és hegesztett kötései [74] esetére. Tekintettel arra, hogy a vizsgált anyagminőségek anyagszerkezettani sajátosságai és mechanikai tulajdonságai széles tartományt fognak át a módszer általános alkalmazhatósága megállapítható. Ötvözetlen acélok és hegesztett kötéseik fáradásos repedésterjedésre érvényes tervezési görbéiben a feszültségintenzitási tényező tartományának küszöbértéke (D Kth) és a Paris-Erdogan összefüggés kitevője (n) az acél szilárdságának növekedtével csökken, a ciklikus törési szívósság (D Kfc) értéke pedig nő. A hegesztett kötések fáradásos repedésterjedésre érvényes tervezési görbéiben a Paris-Erdogan összefüggés kitevője (n) és a ciklikus törési szívósság (D Kfc) értéke egyaránt nagyobb mint az alapanyagra vonatkozó érték. A fáradásos repedésterjedésre érvényes tervezési görbék származtatásának I igénybevételi módban kidolgozott módszere I+II igénybevételi módban is alkalmazható, a feszültségintenzitási tényező tartománya helyett az effektív feszültségintenzitási tényező tartományát (D Keff) kell használni. Ennek alapján a módszer ilyen értelmű általános alkalmazhatósága is megállapítható. A vizsgálatokhoz alkalmazott próbatestek TPB, CT [49] és CTS [59, 60] típusúak voltak. A vizsgálatokra 10 Cr Mo 9 10, KL7D, X80TM, DO76 és QStE690TM jelű acélok alapanyagain, valamint 10 Cr Mo 9 10, 10 Cr Mo 9 10 és GS 18 Cr Mo 9 10, KL7D, továbbá X80TM jelű acélok hegesztett kötésein került sor. Az acélok mellett vizsgálatokat végeztünk ausztemperált gömbgrafitos öntöttvas alapanyagon (ADI), AlMg3, AlMg5 és AlMg4.5Mn alumíniumötvözeteken és hegesztett kötéseiken. Az alapanyagokból készült próbatestek orientációja T-L, L-T, L-S, illetve L-R volt [49], a hegesztett kötések esetében pedig 1-2, 2-1 és 2-3 [50]. Annak érdekében, hogy a repedésszerű hibák hegesztett kötésekben való előfordulási lehetőségeit modellezni lehessen, a bemetszés elhelyezkedését variáltuk, amelyet a 19. ábra szemléltet.
19. ábra: A bemetszések elhelyezkedése a hegesztett kötésekben A különböző technológiai paraméterekkel (elsődlegesen védőgáz(keverék) és hozaganyag átmérő, de azokból következően áramerősség, illetve huzalelőtolási sebesség és hegesztő feszültség is) elkészített hegesztési ömledékekből kimunkált próbatesteken elvégzett vizsgálatok eredményeit, részmintánként és mintánként, az 5. táblázat foglalja össze. 5. táblázat: A különböző technológiai paraméterekkel készített hegesztési ömledékek vizsgálati eredményei (a Paris-Erdogan összefüggés kitevője)
A táblázat adatai és az elvégzett Wilcoxon-próbák alapján megállapítható, hogy az alkalmazott hozaganyag átmérőjének nincs, a védőgáz típusának, pontosabban az Ar komponens jelenlétének van szignifikáns hatása a fáradásos repedésterjedésre. A vizsgálatokból kapott minták statisztikai jellemzőit ezek után a 6. táblázatban mutatjuk be. A minták birtokában azt kerestük, hogy azok milyen eloszlásfüggvényekkel írhatók le. A műszaki gyakorlatban elterjedt normális, a fárasztóvizsgálatok eredményeinek értékelésére használatos logaritmikus normális eloszlások mellett, a törésmechanikai vizsgálatok eredményeinek feldolgozásához alkalmazott három paraméteres Weibull-eloszlással próbálkoztunk. A Shapiro-Wilk, a Kolmogorov-féle egymintás és a c 2-próba [21, 75, 76] alkalmazásával az elméleti és a tapasztalati eloszlás közötti illeszkedést vizsgáltuk, minden próba esetében e =0.05 szignifikanciaszinten. Eredményül azt kaptuk, hogy csak a Weibull-eloszlás esetén fogadható el az illeszkedés minden mintára. Ezek után meghatároztuk a vizsgált anyagi mérőszámok Weibull-eloszlásának függvényeit, amelynek állandóit a [77] közlemény szerint a következő módon jelöltük:
Az állandók meghatározását a maximális regressziós együttható módszerével, ismert (iterált) küszöbparaméter (N0) feltételezésével [78] végeztük el. Az eloszlásfüggvények birtokában, a 20. ábrán látható módszerrel meghatároztuk a vizsgált alapanyagok és hegesztett kötéseik fáradásos repedésterjedésre érvényes tervezési görbéinek paramétereit. 6. táblázat: Az alapanyagokon (aa), hegesztési ömledékeken (hö) és hegesztett kötéseken (hk) elvégzett vizsgálatokból kapott minták statisztikai jellemzői
1) 2-3, T-L/1-2, T-L/2-1, L-T/1-2, L-T/2-1. 2) T-L/1-2, T-L/2-1, L-T/1-2, L-T/2-1. 3) T-L, L-T, L-S. 4) I+II igénybevételi módban. 5) DK helyett DKeff értendő. A Paris-Erdogan összefüggés két állandója közötti kapcsolatot az irodalomban (például [56]) szokásos
alakban kerestük, az eredményeket pedig a 7. táblázatban foglaltuk össze.
20. ábra: Fáradásos repedésterjedésre érvényes tervezési görbék származtatása (elvi ábra) 7. táblázat: A Paris-Erdogan összefüggés két állandója közötti kapcsolatot leíró függvény paraméterei
A 7. táblázatban szereplő állandókkal kapcsolatban említést érdemel, hogy azok jó összhangban vannak az irodalomban [56, 69] közölt értékekkel. A meghatározott tervezési görbék paramétereit a 8. táblázat tartalmazza. 8. táblázat: A fáradásos repedésterjedésre érvényes tervezési görbék paraméterei
1) A hegesztési maradó feszültségek jellegének megítélése és nagyságának becslése után származtatható. 2) 16 mérés átlaga nyomó maradó feszültségek jelenléte esetén: DKth=16.91 MPa m1/2. 3) 2 mérés átlaga: DKth=12.7 MPa m1/2. 4) 3 mérés átlaga: DKth=8.97 MPa m1/2. 5) 4 mérés átlaga nyomó maradó feszültségek jelenléte esetén: DKth=16.29 MPa m1/2. 6) I+II igénybevételi módban. 7) DK helyett DKeff értendő. 8) A három alumíniumötvözetre egy eloszlásfüggvényt határoztunk meg.
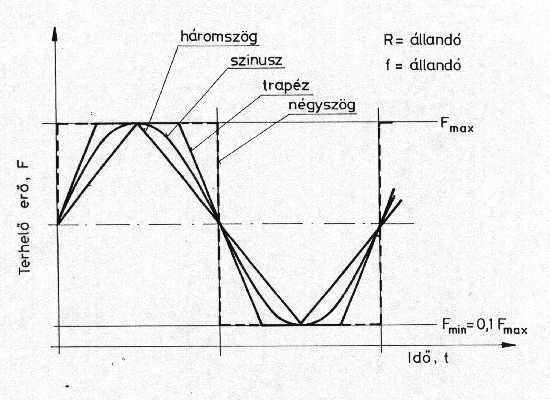
3.4. Fáradásos repedésterjedés különböző alakú terhelési függvények esetén A terhelési függvény alakja – hasonlóan a fáradásos repedésterjedésre ható többi tényezőhöz – a repedésterjedés kinetikai diagramján elkülöníthető három tartományban eltérő módon befolyásol [56, 79, 80]. A DKth értékére a függvényalak alig hat [81], a Paris-Erdogan összefüggés állandóit (II. tartomány) azonban már számottevően befolyásolja, szoros kapcsolatban a terhelési frekvenciával [42, 82]. A függvényalak hatását – különösen magasabb hőmérsékletek esetében – annak alapján ítélik meg, hogy a maximális terhelés milyen hányadában hat a teljes terhelési ciklusnak, illetve milyen a terhelés fel- és lefutása a cikluson belül [82, 83, 84]. A kérdés energetikai jellegű megközelítése kúszás és repedésterjedés kölcsönhatása esetén jellemző [85], míg a különböző anyagminőségek viselkedésének összehasonlítása nem szokásos. A kinetikai diagram III. tartományában a ciklusalak hatása ismét kicsi, s mivel e tartomány szerepe a gyakorlat számára csekély a részletes elemzés nem indokolt. A kutató munka során igazoltuk, hogy a háromszög, a szinusz, a trapéz és a négyszög alakú terhelési függvényekkel elvégzett vizsgálatok eredményeinek (Paris-Erdogan összefüggés kitevője) átlaga a kisebb szilárdságú anyagoknál eltérő, a nagyszilárdságú acélnál nem. A legnagyobb és a legkisebb átlagérték közötti különbség a szilárdság növekedtével csökken. Kimutattuk, hogy a Paris-Erdogan összefüggés kitevőjének (n) átlaga a kisebb szilárdságú anyagoknál az egy terhelési ciklusban térfogategységbe befektetett munka növekedtével csökken, a nagyszilárdságú acélnál nem. Ez a repedés csúcsában kialakuló, a vizsgált anyagminőségek eltérő rugalmas-képlékeny viselkedése következtében különböző képlékeny zónával magyarázható. A vizsgálatokhoz alkalmazott próbatestek TPB [49] típusúak voltak, s a vizsgálatokra Armco-vas, KL7D, valamint X80TM alapanyagokon került sor. A próbatestek orientációja anyagminőségenként azonos volt, az Armco-vas esetében L-T, a KL7D és az X80TM jelű acélok esetében pedig L-S [49]. Az alkalmazott terhelési függvények idealizált alakját a 21. ábra szemlélteti. Tekintettel arra, hogy a vizsgálatokra kis terhelési frekvenciával (f=5 Hz) került sor, az idealizált alaktól való eltérés a trapéz és a négyszög alakú függvények esetében sem volt jelentős.
21. ábra: A háromszög, szinusz, trapéz és négyszög alakú terhelési függvények A 22. és a 23. ábrán erő-szétnyílás görbék láthatók Armco-vasból készült próbatestek vizsgálataiból, példaként. A terhelési függvény a 22. ábrán szemléltetett esetben háromszög, a 23. ábrán bemutatott példában pedig trapéz alakú volt. A vizsgálati eredményekből – a Paris-Erdogan összefüggés kitevője (n) – anyagminőségenként és terhelési függvényenként képzett minták jellemzőit a 8. táblázat foglalja össze. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
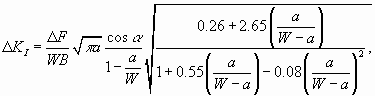 (3)
(3)
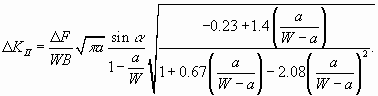 (4)
(4)
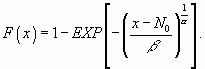 (5)
(5)